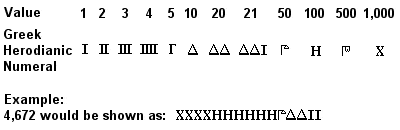
Números herodíacos gregos antigos
Como o império grego começou a espalhar a sua esfera de influência pela Ásia Menor, Mesopotâmia e mais além, os gregos foram suficientemente inteligentes para adotar e adaptar elementos úteis das sociedades que conquistaram. Isto era tão verdadeiro para a matemática deles como qualquer outra coisa, e eles adotaram elementos da matemática tanto dos babilônios quanto dos egípcios. Mas logo começaram a fazer contribuições importantes por direito próprio e, pela primeira vez, podemos reconhecer as contribuições dos indivíduos. No período helenístico, os gregos tinham presidido a uma das revoluções mais dramáticas e importantes do pensamento matemático de todos os tempos.
Numerais áticos ou herodianos
O antigo sistema de numerais gregos, conhecido como sótão ou números herodianos, foi totalmente desenvolvido por cerca de 450 a.C., e em uso regular possivelmente já no século VII a.C. Era um sistema base 10 semelhante ao antigo sistema egípcio (e ainda mais semelhante ao sistema romano posterior), com símbolos para 1, 5, 10, 50, 100, 500 e 1.000 repetidos tantas vezes quantas as necessárias para representar o número desejado. A adição foi feita totalizando separadamente os símbolos (1s, 10s, 100s, etc) nos números a serem adicionados, e a multiplicação foi um processo trabalhoso baseado em duplicações sucessivas (a divisão foi baseada no inverso deste processo).
Teoria da Intercepção de Thales
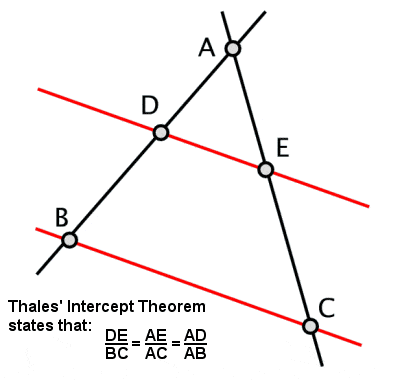
Teoria da Intercepção de Thales
Mas a maior parte da matemática grega foi baseada na geometria. Thales, um dos Sete Sábios da Grécia Antiga, que viveu na costa jónica da Ásia Menor na primeira metade do século VI a.C., é geralmente considerado como tendo sido o primeiro a estabelecer directrizes para o desenvolvimento abstracto da geometria, embora o que sabemos do seu trabalho (como em triângulos rectos e semelhantes) pareça agora bastante elementar.
Thales estabeleceu o que ficou conhecido como Teorema de Thales, onde se um triângulo é desenhado dentro de um círculo com o lado longo como diâmetro do círculo, então o ângulo oposto será sempre um ângulo reto (assim como algumas outras propriedades relacionadas derivadas disso). Ele também é creditado com outro teorema, também conhecido como Teorema de Thales ou Teorema de Intercepção, sobre as proporções dos segmentos de linha que são criados se duas linhas de intersecção forem interceptadas por um par de paralelos (e, por extensão, as proporções dos lados de triângulos semelhantes).
Até certo ponto, porém, a lenda do matemático Pitágoras de Samos do século VI a.C. tornou-se sinônimo do nascimento da matemática grega. Na verdade, acredita-se que ele tenha cunhado tanto as palavras “filosofia” (“amor à sabedoria”) como “matemática” (“aquilo que é aprendido”). Pitágoras foi talvez o primeiro a perceber que um sistema completo de matemática podia ser construído, onde os elementos geométricos correspondiam aos números. O Teorema de Pitágoras (ou o Teorema de Pitágoras) é um dos mais conhecidos de todos os teoremas matemáticos. Mas ele continua sendo uma figura controversa, como veremos, e a matemática grega não estava de forma alguma limitada a um homem.
Três problemas geométricos
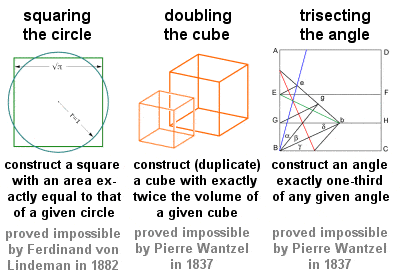
Os Três Problemas Clássicos
Três problemas geométricos em particular, muitas vezes referidos como os Três Problemas Clássicos, e todos a serem resolvidos por meios puramente geométricos usando apenas uma borda reta e uma bússola, datam dos primeiros dias da geometria grega: “o quadrado (ou quadratura) do círculo”, “a duplicação (ou duplicação) do cubo” e “a trissecção de um ângulo”. Estes problemas intransigentes influenciaram profundamente a geometria futura e levaram a muitas descobertas frutíferas, embora as suas soluções actuais (ou, como se verificou, as provas da sua impossibilidade) tivessem de esperar até ao século XIX.
Hipócrates de Chios (não confundir com o grande médico grego Hipócrates de Kos. Uma biografia detalhada aqui.) foi um desses matemáticos gregos que se aplicou a esses problemas durante o século V a.C. (sua contribuição para o problema da “quadratura do círculo” é conhecida como a Luna de Hipócrates). Seu influente livro “Os Elementos”, datado de cerca de 440 a.C., foi a primeira compilação dos elementos da geometria, e sua obra foi uma importante fonte para o trabalho posterior de Euclides.
Paradoxo de Aquiles e da Tartaruga de Zeno
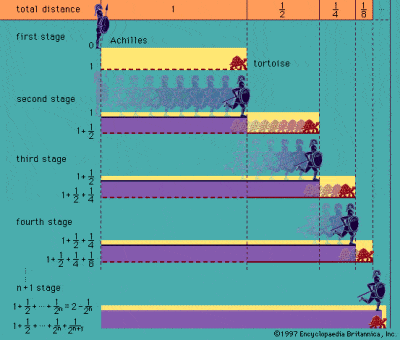
Paradoxo de Aquiles e da Tartaruga de Zeno
Foram os gregos os primeiros a lutar com a ideia do infinito, tal como descrito nos conhecidos paradoxos atribuídos ao filósofo Zeno de Elea no século V a.C. O mais famoso dos seus paradoxos é o de Aquiles e a Tartaruga, que descreve uma corrida teórica entre Aquiles e uma tartaruga. Aquiles dá um avanço à tartaruga muito mais lenta, mas quando Aquiles atinge o ponto de partida da tartaruga, a tartaruga já se adiantou. Quando Aquiles chega a esse ponto, a tartaruga já avançou novamente, etc, etc, de modo que em princípio o rápido Aquiles nunca poderá alcançar a tartaruga lenta.
Paradoxes como este e o chamado Paradoxo da dicotomia de Zeno são baseados na infinita divisibilidade do espaço e do tempo, e descansam sobre a idéia de que um meio mais um quarto mais um oitavo mais um décimo sexto, etc, etc, até o infinito nunca será igual a um todo. O paradoxo decorre, no entanto, da falsa suposição de que é impossível completar um número infinito de traços discretos num tempo finito, embora seja extremamente difícil provar definitivamente a falácia. O antigo Aristóteles grego foi o primeiro de muitos a tentar refutar os paradoxos, particularmente por acreditar firmemente que o infinito só poderia ser potencial e não real.
Democrata, mais famoso pelas suas ideias prescientes sobre toda a matéria ser composta de pequenos átomos, foi também um pioneiro da matemática e geometria no século V-4 a.C., e produziu obras com títulos como “Sobre Números”, “Sobre Geometria”, “Sobre Tangências”, “Sobre Mapeamento” e “Sobre Irracionais”, embora estas obras não tenham sobrevivido. Sabemos que ele foi um dos primeiros a observar que um cone (ou pirâmide) tem um terço do volume de um cilindro (ou prisma) com a mesma base e altura, e ele é talvez o primeiro a considerar seriamente a divisão dos objetos em um número infinito de seções transversais.
No entanto, é certamente verdade que Pitágoras em particular influenciou muito aqueles que vieram depois dele, incluindo Platão, que estabeleceu a sua famosa Academia em Atenas em 387 a.C., e o seu protegido Aristóteles, cujo trabalho de lógica foi considerado definitivo por mais de dois mil anos. Platão o matemático é mais conhecido pela sua descrição dos cinco sólidos platônicos, mas o valor do seu trabalho como professor e popularizador de matemática não pode ser exagerado.
O aluno de Platão Eudoxus de Cnidus é geralmente creditado com a primeira implementação do “método de exaustão” (mais tarde desenvolvido por Arquimedes), um método precoce de integração por aproximações sucessivas que ele utilizou para o cálculo do volume da pirâmide e do cone. Ele também desenvolveu uma teoria geral de proporção, aplicável às magnitudes incomensuráveis (irracionais) que não podem ser expressas como uma razão de dois números inteiros, bem como às magnitudes comensuráveis (racionais), ampliando assim as idéias incompletas de Pitágoras.
Talvez a contribuição única mais importante dos gregos – e Pitágoras, Platão e Aristóteles foram todos influentes a este respeito – foi a idéia de prova, e o método dedutivo de usar passos lógicos para provar ou refutar teoremas dos axiomas iniciais assumidos. As culturas mais antigas, como os egípcios e os babilónios, tinham confiado no raciocínio indutivo, ou seja, na utilização de observações repetidas para estabelecer regras de ouro. É este conceito de prova que dá à matemática o seu poder e assegura que as teorias comprovadas são tão verdadeiras hoje como eram há dois mil anos atrás, e que lançou as bases para a abordagem sistemática da matemática de Euclides e daqueles que vieram depois dele.
| < < De volta à Matemática Egípcia | Em frente a Pitágoras >> |