Método Delta-Delta Ct ou método Livak é o método mais preferido para análise de dados qPCR. No entanto, ele só pode ser usado quando determinados critérios são cumpridos. Consulte as notas da palestra para certificar-se de que esses critérios sejam cumpridos. Caso contrário, um método mais generalizado é chamado de método Pfaffl. Por favor, leia o material de leitura adicional para obter mais informações sobre este método.
Aqui estão os passos do método Livak:
O arquivo Excel com todos os cálculos está na pasta de análise qPCR no Blackboard.
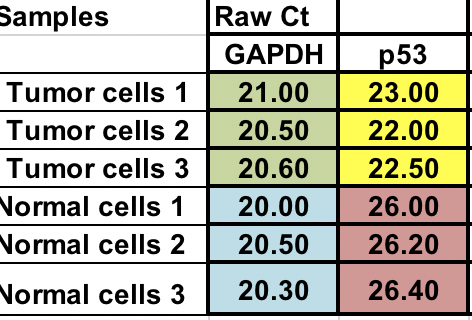
Você tem Ct bruto (número de ciclos que leva para atingir o limiar) para células normais e tumorais (3 réplicas para cada).
Normalização¶
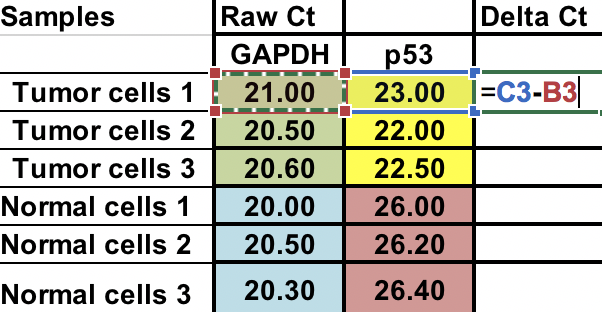
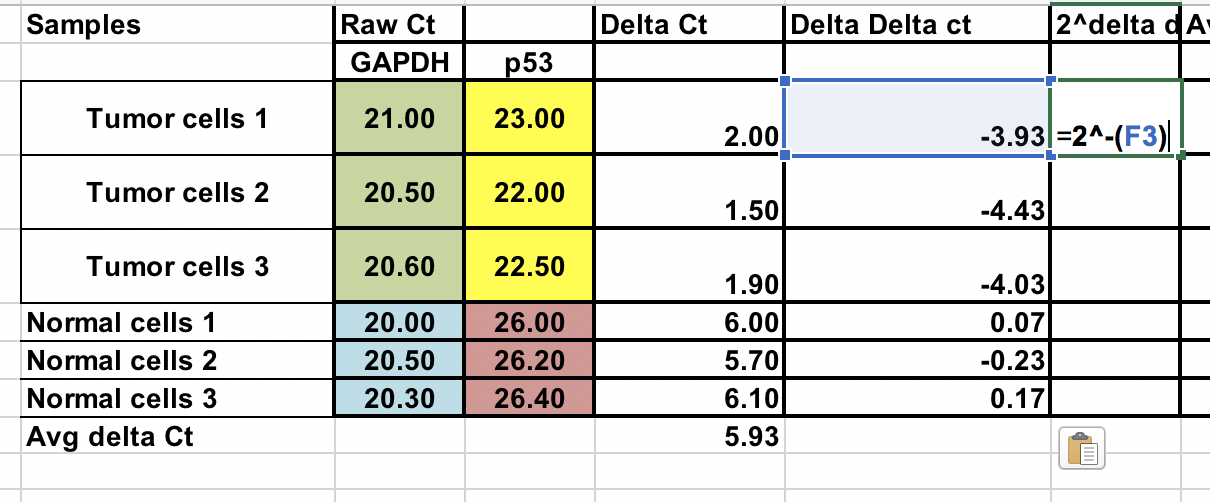
Primeiro, você precisará calcular a diferença relativa entre o gene de interesse (p53) e o gene home keep (GAPDH).
∆Ct = Ct (gene de interesse) – Ct (gene homekeeping)
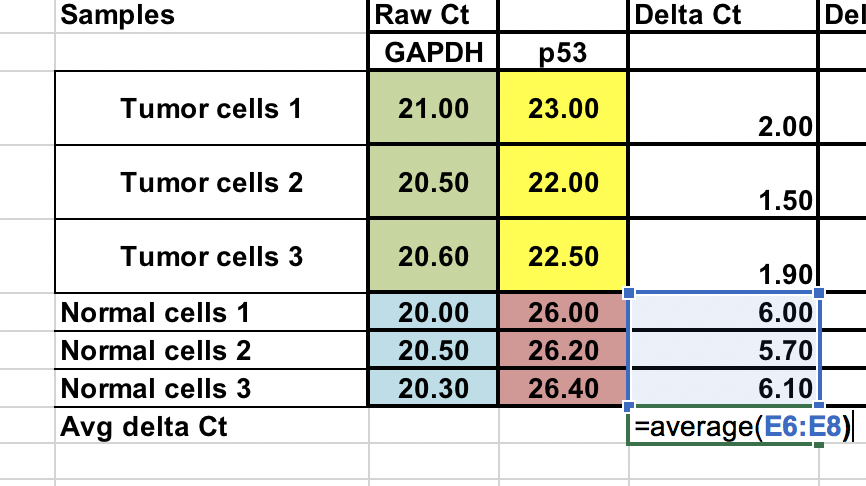
Média das amostras de controle (células normais)¶
Como comparamos nosso tumor (tratamento) ao controle (células normais), primeiro precisamos de uma média de ∆Ct para as 3 amostras de controlo (normais).
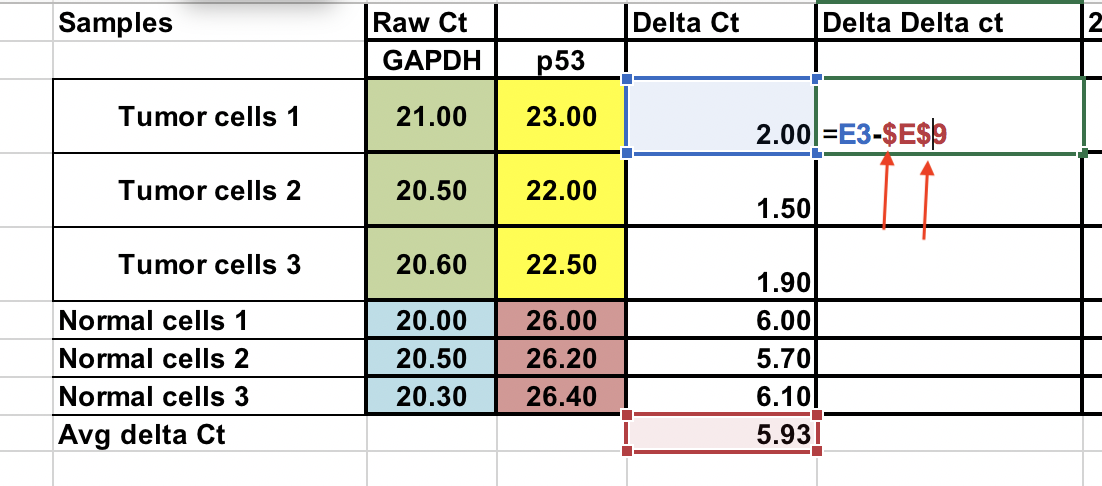
Calcule a ∆∆Ct em relação à média de ∆Ct normal células¶
∆∆Ct = ∆Ct (amostra tumoral) – ∆Ct (média normal)
Você também pode fazer isso com amostras normais. Use sinais $ de violação do número da coluna e letra bruta (setas) para fixar a célula.
Expressão do gene dobrado para cada amostra.
Expressão do gene dobrado = 2^-(∆∆Ct)
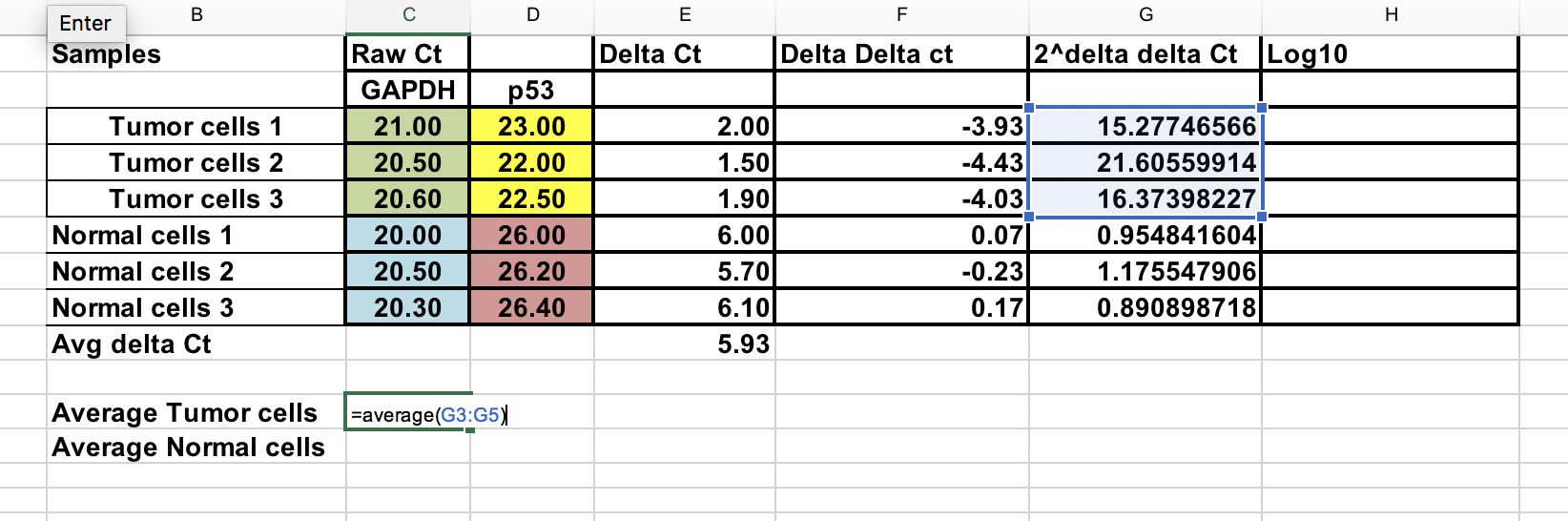
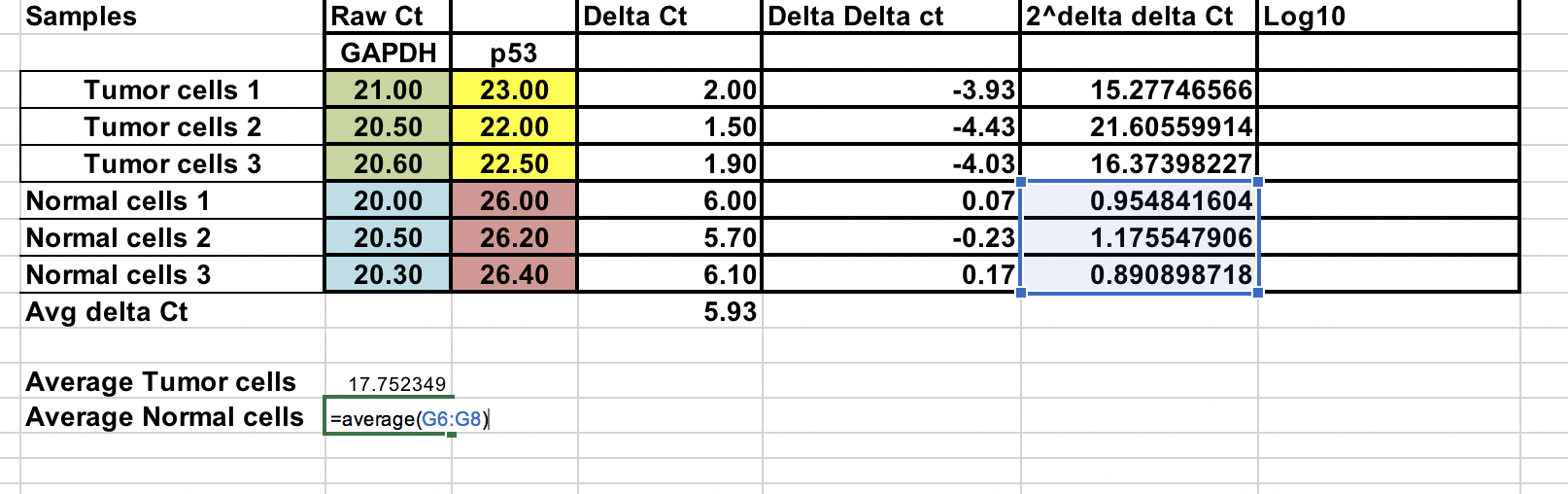
Mudança de dobras em todas as dobras¶
Pode calcular a mudança média de dobras tanto para amostras tumorais como normais. Relação entre estas duas dobras a mudança de dobra entre as amostras tumorais e normais.
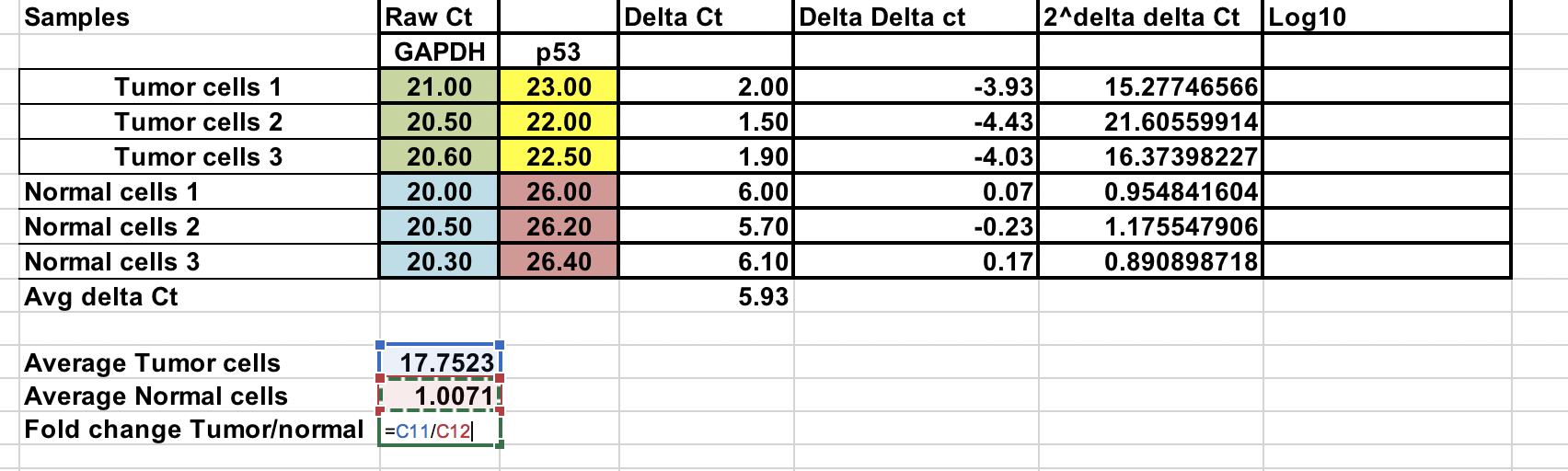
Transformação de log #
Para realizar testes estatísticos paramétricos como o teste T, é aconselhável transformar os resultados finais da expressão gênica em valores de log (qualquer base de log). Isto faria a distribuição dos dados simétrica.
Aqui temos que mudar o 2^-(∆∆Ct) para log 10.
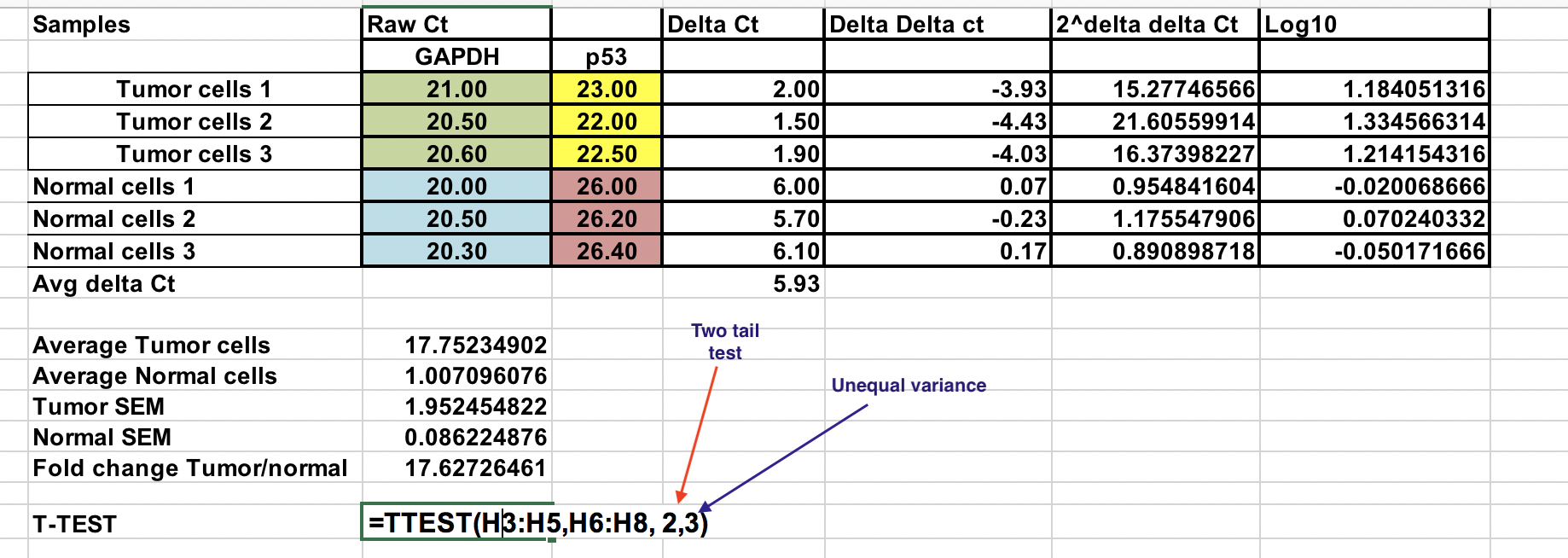
T-test¶
Need para ter cuidado ao usar testes paramétricos se os dados não são normalmente distribuídos, isso levaria a conclusões erradas.
Select log 10 of 2^-(∆∆Ct) values for Normal and tumor samples as indicated. Use dois testes de cauda (número 2) e assumindo uma variância desigual (3).
Resultando o valor de P menor que 0,05 e, portanto, rejeitamos a hipótese nula e duas médias de amostra são significativamente diferentes ao nível 0,05.