Diagramas de blocos constituídos por um único bloco ou uma combinação de blocos. Estes são usados para representar os sistemas de controle em forma pictórica.
Elementos básicos do diagrama de blocos
Os elementos básicos de um diagrama de blocos são um bloco, o ponto de soma e o ponto de decolagem. Consideremos o diagrama de blocos de um sistema de controle em malha fechada como mostrado na figura seguinte para identificar esses elementos.
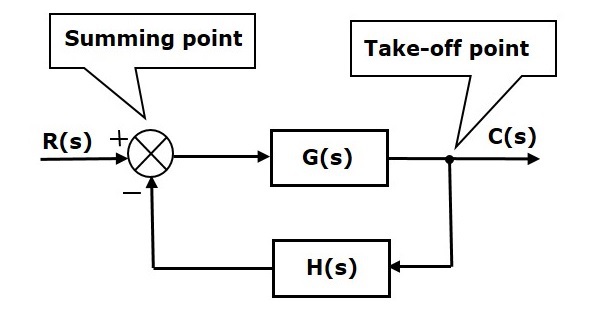
O diagrama de blocos acima consiste em dois blocos com funções de transferência G(s) e H(s). Também possui um ponto de somatória e um ponto de decolagem. As setas indicam o sentido do fluxo dos sinais. Vamos agora discutir estes elementos um por um.
Block
A função de transferência de um componente é representada por um bloco. O bloco tem uma única entrada e saída.
A figura seguinte mostra um bloco com entrada X(s), saída Y(s) e a função de transferência G(s).

Função de transferência,$G(s)=\frac{Y(s)}{X(s)}$
$$$\Função de transferência,$G(s)X(s)$$
A saída do bloco é obtida multiplicando a função de transferência do bloco com a entrada.
Ponto de soma
O ponto de soma é representado com um círculo que tem uma cruz (X) dentro dele. Possui duas ou mais entradas e uma saída. Ele produz a soma algébrica das entradas. Também realiza a soma ou subtração ou combinação da soma e subtração das entradas com base na polaridade das entradas. Vejamos estas três operações uma a uma.
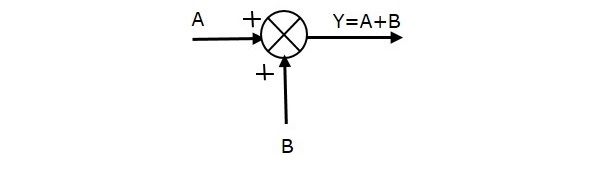
A figura seguinte mostra o ponto de soma com duas entradas (A, B) e uma saída (Y). Aqui, as entradas A e B têm um sinal positivo. Assim, o ponto de somatória produz a saída, Y como soma de A e B.
i.e.,Y = A + B.
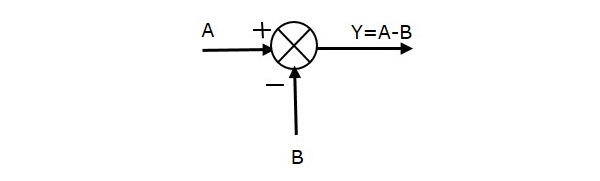
A figura seguinte mostra o ponto de somatória com duas entradas (A, B) e uma saída (Y). Aqui, as entradas A e B estão tendo sinais opostos, ou seja, A está tendo sinal positivo e B está tendo sinal negativo. Assim, o ponto de soma produz a saída Y como a diferença de A e B.
Y = A + (-B) = A – B.
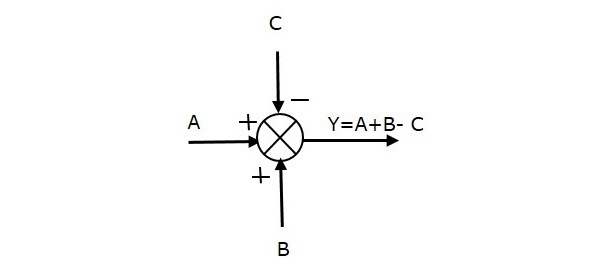
A figura seguinte mostra o ponto de soma com três entradas (A, B, C) e uma saída (Y). Aqui, as entradas A e B estão tendo sinais positivos e C está tendo um sinal negativo. Então, o ponto de soma produz a saída Y como
Y = A + B + (-C) = A + B – C.
 >
>
Ponto de Tomada
Ponto de Tomada é um ponto a partir do qual o mesmo sinal de entrada pode ser passado por mais de um ramo. Isso significa que com a ajuda do ponto de descolagem, podemos aplicar a mesma entrada a um ou mais blocos, somando pontos.
Na figura seguinte, o ponto de descolagem é usado para ligar a mesma entrada, R(s) a mais dois blocos.
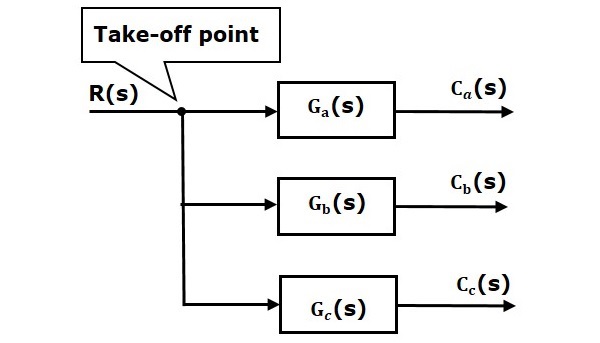
Na figura seguinte, o ponto de descolagem é utilizado para ligar a(s) saída(s) C, como uma das entradas ao ponto de soma.
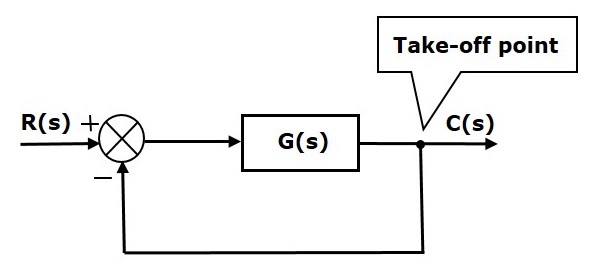
Representação do Diagrama de Bloco dos Sistemas Eléctricos
Nesta secção, vamos representar um sistema eléctrico com um diagrama de blocos. Os sistemas elétricos contêm principalmente três elementos básicos – resistência, indutor e capacitor.
Considerar uma série de circuitos RLC como mostra a figura a seguir. Onde, Vi(t) e Vo(t) são as tensões de entrada e saída. Deixe i(t) ser a corrente que atravessa o circuito. Este circuito está no domínio do tempo.
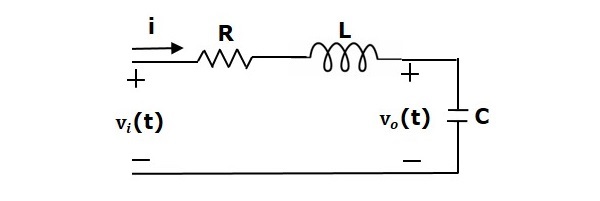
Ao aplicar a transformada Laplace a este circuito, obterá o circuito em s-domínio. O circuito é como mostrado na figura abaixo.
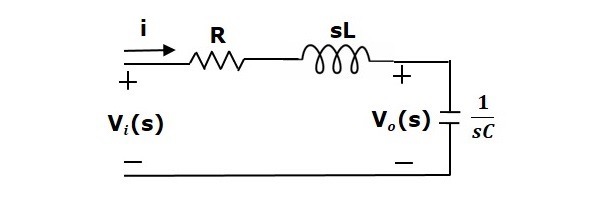
Do circuito acima, podemos escrever
$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$
$$$\i(s)=esquerda { \i(1}{R+sL} \direita esquerda ( V_i(s)-V_o(s)-V_o(s) direita $ (Equação 1)
$V_o(s)=esquerda ( Frac{1}{sC} {1}direita )I(s)$ (Equação 2)
Deixe-nos agora desenhar os diagramas de blocos para estas duas equações individualmente. E então combinem esses diagramas de blocos corretamente para obter o diagrama de blocos geral das séries do Circuito RLC (s-domínio).
Equação 1 pode ser implementada com um bloco com a função de transferência, $\frac{1}{R+sL}$. A entrada e saída deste bloco são $\i(s)-V_o(s) { V_i(s)-V_o(s) {direita }$ e $I(s)$. Precisamos de um ponto de somatório para obter $es $esquerda. O diagrama de blocos da Equação 1 é mostrado na seguinte figura.
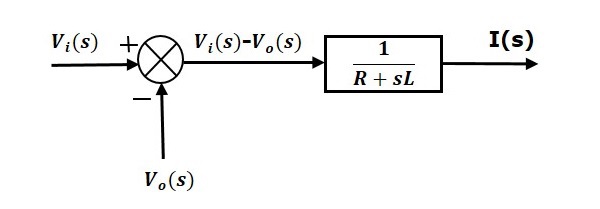
Equação 2 pode ser implementada com um bloco com função de transferência, $\frac{1}{sC}$. A entrada e saída deste bloco são $I(s)$ e $V_o(s)$. O diagrama de blocos da Equação 2 é mostrado na figura seguinte.
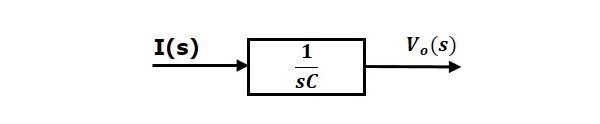
O diagrama de blocos geral da série de circuitos RLC (s-domínio) é mostrado na figura seguinte.
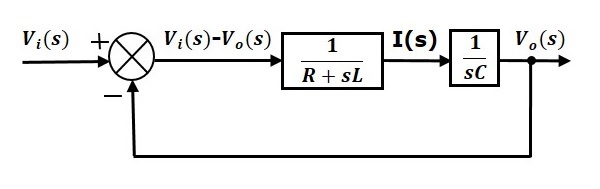
Simplesmente, você pode desenhar o diagrama de blocos de qualquer circuito elétrico ou sistema apenas seguindo este simples procedimento.
-
Converta o circuito elétrico do domínio do tempo em um circuito elétrico do domínio s, aplicando a transformada Laplace.
-
Enumerar as equações para a corrente que passa por todos os elementos de derivação em série e tensão através de todos os ramos de derivação.
-
Desenhar os diagramas de blocos para todas as equações acima individualmente.
-
Combinar adequadamente todos estes diagramas de blocos para obter o diagrama de blocos global do circuito elétrico (s-domínio).