Introducere
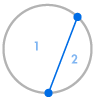
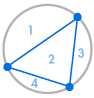
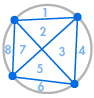
Imaginați-vă că așezăm mai multe puncte pe circumferința unui cerc și conectăm fiecare punct între ele. Acest lucru împarte cercul în mai multe regiuni diferite, iar noi putem număra numărul de regiuni în fiecare caz. Diagramele de mai jos arată câte regiuni există pentru mai multe numere diferite de puncte de pe circumferință. Trebuie să ne asigurăm că doar două linii se întâlnesc la fiecare intersecție în interiorul cercului, nu trei sau mai multe.
 |
 |
 |
 |
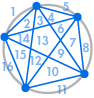 |
| 1 regiune | 2 regiuni | 4 regiuni | 8 regiuni | 16 regiuni |
Se poate observa imediat un tipar: numărul de regiuni este întotdeauna de două ori mai mare decât cel precedent, astfel încât obținem secvența 1, 2, 4, 8, 16, … Aceasta înseamnă că cu 6 puncte pe circumferință ar fi 32 de regiuni, iar cu 7 puncte ar fi 64 de regiuni.
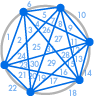
Am putea decide că suntem mulțumiți de acest rezultat. Numărul de regiuni este întotdeauna de două ori mai mare decât cel anterior – la urma urmei, acest lucru a funcționat pentru primele cinci cazuri. Sau am putea decide că ar trebui să mai verificăm câteva, doar pentru a fi siguri:
 |
 |
| 31 regiuni, nu 32 | 57 regiuni, nu 64 |
Din păcate, ceva a mers prost: 31 ar putea părea o greșeală de numărare, dar 57 este mult mai puțin decât 64. Secvența continuă 99, 163, 256, …, foarte diferit de ceea ce am obține la dublarea numărului anterior.
Acest exemplu ilustrează de ce, în matematică, nu poți spune că o observație este întotdeauna adevărată doar pentru că funcționează în câteva cazuri pe care le-ai testat. În schimb, trebuie să vii cu un argument logic riguros care să ducă de la rezultatele pe care le cunoști deja, la ceva nou pe care vrei să demonstrezi că este adevărat. Un astfel de argument se numește demonstrație.
Demonstrațiile sunt ceea ce face ca matematica să fie diferită de toate celelalte științe, deoarece, odată ce am demonstrat ceva, suntem absolut siguri că este și va fi întotdeauna adevărat. Nu este doar o teorie care se potrivește observațiilor noastre și care poate fi înlocuită de o teorie mai bună în viitor.
În exemplul de mai sus, am putea număra numărul de intersecții din interiorul cercului. Gândindu-ne cu atenție la relația dintre numărul de intersecții, linii și regiuni, vom ajunge în cele din urmă la o altă ecuație pentru numărul de regiuni atunci când există x = V.Axi puncte pe cerc:
Numărul de regiuni = x4 – 6 x3 + 23 x2 – 18 x + 2424 = (Math.pow(V.Axi,4) – 6*Math.pow(V.Axi,3) + 23*Math.pow(V.Axi,2) – 18*V.Axi + 24)/24.
Această ecuație funcționează în toate cazurile de mai sus. Am putea acum să încercăm să o demonstrăm pentru fiecare valoare a lui x folosind „inducția”, o tehnică explicată mai jos.
În mod tradițional, sfârșitul unei demonstrații este indicat folosind un ■ sau □, sau scriind QED sau „quod erat demonstrandum”, ceea ce în latină înseamnă „ceea ce trebuia demonstrat”.
Un rezultat sau o observație despre care credem că este adevărat se numește Ipoteză sau Conjectură. Odată ce am demonstrat-o, o numim Teoremă. Odată ce am demonstrat o teoremă, o putem folosi pentru a demonstra alte rezultate mai complicate – construind astfel o rețea crescândă de teoreme matematice.
Axiome

Școala de la Atena a lui Raphael: matematicienii greci antici au fost primii care au abordat matematica folosind un cadru logic și axiomatic.
O întrebare interesantă este de unde să începem. Cum demonstrezi prima teoremă, dacă nu știi încă nimic? Din păcate, nu poți demonstra ceva folosind nimic. Ai nevoie de cel puțin câteva elemente de bază cu care să începi, iar acestea se numesc axiome.
Matematicienii presupun că axiomele sunt adevărate fără a putea să le demonstreze. Cu toate acestea, acest lucru nu este atât de problematic pe cât pare, deoarece axiomele sunt fie definiții, fie clar evidente, și există doar foarte puține axiome. De exemplu, o axiomă ar putea fi că a + b = b + a pentru oricare două numere a și b.
Axiomele sunt importante pentru a fi corecte, deoarece întreaga matematică se bazează pe ele. Dacă există prea puține axiome, se pot demonstra foarte puține lucruri și matematica nu ar fi foarte interesantă. Dacă există prea multe axiome, se poate demonstra aproape orice și, de asemenea, matematica nu ar fi interesantă. De asemenea, nu puteți avea axiome care să se contrazică între ele.
Matematica nu se referă la alegerea setului corect de axiome, ci la dezvoltarea unui cadru de lucru pornind de la aceste puncte de plecare. Dacă începeți cu axiome diferite, veți obține un tip diferit de matematică, dar argumentele logice vor fi aceleași. Fiecare domeniu al matematicii are propriul set de axiome de bază.
Când matematicienii au demonstrat o teoremă, ei o publică pentru ca alți matematicieni să o verifice. Uneori ei găsesc o greșeală în argumentul logic, iar alteori o greșeală nu este găsită decât mulți ani mai târziu. Cu toate acestea, în principiu, este întotdeauna posibilă descompunerea unei demonstrații în axiomele de bază.
Teoria seturilor și axioma alegerii

Pentru a formula demonstrații este uneori necesar să ne întoarcem la însăși fundamentul limbajului în care este scrisă matematica: teoria seturilor.
Un set este o colecție de obiecte, cum ar fi numerele. Elementele unui set sunt de obicei scrise în paranteze curbe. Putem găsi uniunea a două seturi (setul de elemente care se află în oricare dintre seturi) sau putem găsi intersecția a două seturi (setul de elemente care se află în ambele seturi).
Multe probleme matematice pot fi formulate în limbajul teoriei seturilor, iar pentru a le demonstra avem nevoie de axiomele teoriei seturilor. De-a lungul timpului, matematicienii au folosit diverse colecții diferite de axiome, cele mai larg acceptate fiind cele nouă axiome Zermelo-Fraenkel (ZF):
AXIOMĂ DE EXTINDERE
Dacă două seturi au aceleași elemente, atunci ele sunt egale.
AXIOMUL SEPARAȚIEI
Se poate forma un subansamblu al unui ansamblu, care este format din anumite elemente.

AXIOMUL DE SEPARARE A ANSAMBLURILOR
Există un ansamblu fără membri, scris ca {} sau ∅.
AXIOMUL ANSAMBLURILOR
Date două obiecte x și y putem forma un ansamblu {x, y}.
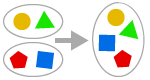
AXIOMUL UNIRII
Se poate forma uniunea a două sau mai multe ansambluri.
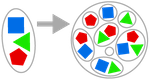
AXIOMUL ANSAMBLULUI PUTERNIC
După un ansamblu oarecare, putem forma ansamblul tuturor subansamblurilor (ansamblul puterii).
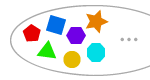
AXIOMUL INFINITĂȚII
Există un ansamblu cu infinit de multe elemente.

AXIOM DE FUNDAMENTARE
Seturile se construiesc din seturi mai simple, ceea ce înseamnă că fiecare set (nevid) are un membru minim.
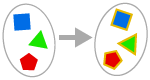
AXIOMĂ DE ÎNLOCUIRE
Dacă aplicăm o funcție fiecărui element dintr-un set, răspunsul este tot un set.
Dacă vă gândiți la teoria seturilor, majoritatea acestor axiome vor părea complet evidente – și asta este ceea ce ar trebui să fie axiomele. Cu toate acestea, există o a zecea axiomă care este ceva mai problematică:
AXIOMĂ DE ALEGERE
Date fiind infinit de multe seturi nevide, puteți alege un element din fiecare dintre aceste seturi.
La prima vedere, axioma de alegere (AC) pare la fel de inocentă ca și celelalte de mai sus. Cu toate acestea, utilizarea infinitului are o serie de consecințe neașteptate. De exemplu, puteți folosi AC pentru a demonstra că este posibil să tăiați o sferă în cinci bucăți și să le reasamblați pentru a obține două sfere, fiecare identică cu sfera inițială. Acesta este doar un concept teoretic – tăieturile necesare sunt fractale, ceea ce înseamnă că nu pot exista de fapt în viața reală, iar unele dintre piese sunt „nemăsurabile”, ceea ce înseamnă că nu au un volum definit. Dar faptul că axioma alegerii poate fi folosită pentru a construi aceste tăieturi imposibile este destul de îngrijorător.
Există o dezbatere pasionată în rândul logicienilor, dacă să accepte sau nu axioma alegerii. Fiecare colecție de axiome formează o mică „lume matematică”, iar teoreme diferite pot fi adevărate în lumi diferite. Este de fapt doar o chestiune de a ști dacă ești fericit să trăiești într-o lume în care poți face două sfere dintr-o singură…
Proba prin inducție
Proba prin inducție este o tehnică ce poate fi folosită pentru a demonstra că o anumită afirmație este adevărată pentru toate numerele naturale 1, 2, 3, … „Afirmația” este de obicei o ecuație sau o formulă care include o variabilă n care poate fi orice număr natural. Să notăm afirmația aplicată lui n prin S(n). Iată cei patru pași ai inducției matematice:
- Prima dată demonstrăm că S(1) este adevărată, adică că enunțul S este adevărat pentru 1.
- Acum presupunem că S(k) este adevărată, adică că enunțul S este adevărat pentru un număr natural k.
- Utilizând această presupunere, încercăm să deducem că S(k + 1) este de asemenea adevărată. Astfel, ori de câte ori S este adevărată pentru un număr, ea este adevărată și pentru următorul număr.
- Din moment ce știm că S(1) este adevărată, S(2) trebuie să fie adevărată. Și, prin urmare, S(3) trebuie să fie adevărat. Și, prin urmare, S(4) trebuie să fie adevărat. Și așa mai departe: S trebuie să fie adevărat pentru toate numerele.

Inducția poate fi comparată cu piesele de domino care cad: ori de câte ori cade o piesă de domino, cade și următoarea. Primul pas, dovedind că S(1) este adevărat, începe reacția în lanț infinit.
Primul pas este adesea trecut cu vederea, deoarece este atât de simplu. De fapt, este foarte important și întregul lanț de inducție depinde de el – după cum vor arăta câteva dintre exemplele următoare…
Obiectivul jocului Towers of Hanoi este de a muta un număr de discuri de la un cuier la altul. Nu aveți voie să mutați decât câte un singur disc odată și nu aveți voie să puneți un disc mai mare deasupra unuia mai mic. Încercați să mutați turnul de discuri de la primul cuier la ultimul cuier, cu cât mai puține mutări posibile:
Număr de discuri: Start Over Mișcări: 0
După ce am înțeles regulile jocului, putem încerca să găsim cel mai mic număr de pași necesari, dat fiind orice număr de discuri. Jucându-ne cu jocul de mai sus am putea observa că, cu n discuri, este nevoie de cel puțin 2n – 1 pași. Să numim această afirmație S(n).
S(1) este în mod clar adevărată, deoarece, cu un singur disc, aveți nevoie doar de o singură mutare, iar 21 – 1 = 1.
Să presupunem acum că S(k) este adevărată, adică că aveți nevoie de 2k – 1 pași pentru k discuri. Atunci, dacă avem k + 1 discuri:
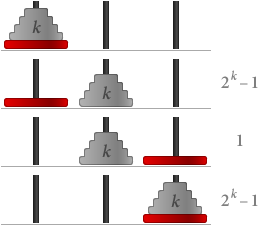
În total avem nevoie de (2k – 1) + 1 + (2k – 1) = 2(k+1) – 1 pași. Aceasta înseamnă că S(k + 1) este de asemenea adevărată.
Prin inducție matematică, S(n) este adevărată pentru toate valorile lui n, ceea ce înseamnă că cel mai eficient mod de a muta n = V.Hanoi discuri necesită 2n – 1 = Math.pow(2,V.Hanoi)-1 mișcări. ■
Să folosim inducția pentru a demonstra că suma primelor n numere naturale este n (n + 1)2. Verificăm mai întâi ecuația pentru valori mici ale lui n:
1 = 1 (1 + 1)2.
1 + 2 = 2 (2 + 1)2 = 3.
În continuare, presupunem că rezultatul este adevărat pentru k, adică că 1 + 2 + … + k = k (k + 1)2, unde k este un număr pe care nu îl precizăm. Acum
1 + 2 + … + k + (k + 1) = k (k + 1)2 + (k + 1) = (k + 1) (k + 2)2 = (k + 1) 2.
Tocmai am demonstrat că, dacă ecuația este adevărată pentru un anumit k, atunci este adevărată și pentru k + 1. Prin inducție matematică, ecuația este adevărată pentru toate valorile lui n. ■
Există o altă modalitate inteligentă de a demonstra ecuația de mai sus, care nu folosește inducția. Se presupune că Carl Friedrich Gauss (1777 – 1855), unul dintre cei mai mari matematicieni din istorie, a descoperit această metodă în școala primară, când profesorul său i-a cerut să adune toți numerele întregi de la 1 la 100.
Utilizând inducția, dorim să demonstrăm că toate ființele umane au aceeași culoare a părului. Fie S(n) afirmația că „orice grup de n ființe umane are aceeași culoare a părului”.
Este clar că S(1) este adevărată: în orice grup de doar unul, toată lumea are aceeași culoare a părului.
Să presupunem acum S(k), că în orice grup de k toată lumea are aceeași culoare a părului. Dacă înlocuim pe oricine din grup cu altcineva, ei tot fac un total de k și, prin urmare, au aceeași culoare a părului. Acest lucru funcționează pentru orice grup inițial de persoane, ceea ce înseamnă că orice grup de k + 1 are, de asemenea, aceeași culoare a părului. Prin urmare, S(k + 1) este adevărată.
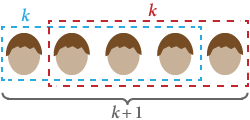
Prin inducție matematică, toate ființele umane au aceeași culoare a părului! ■
Evident, ceva trebuie să fi greșit în demonstrația de mai sus – la urma urmei, nu toată lumea are aceeași culoare a părului. Puteți găsi greșeala?
Unele teoreme nu pot fi dovedite cu adevărat folosind inducția – trebuie să folosim o versiune ușor modificată numită inducție puternică. În loc să presupunem S(k) pentru a demonstra S(k + 1), presupunem toate S(1), S(2), … S(k) pentru a demonstra S(k + 1). Tot ceea ce poate fi demonstrat cu ajutorul inducției (slabe) poate fi demonstrat în mod clar și cu ajutorul inducției puternice, dar nu și invers.
Teorema fundamentală a aritmeticii afirmă că orice număr întreg mai mare decât 1 este fie un număr prim, fie poate fi scris ca produs de numere prime într-un mod esențial unic.
Putem demonstra părți din el folosind inducția puternică: fie S(n) afirmația că „numărul întreg n este un număr prim sau poate fi scris ca produs de numere prime”. S(1) este o excepție, dar S(2) este în mod clar adevărată, deoarece 2 este un număr prim.
Să presupunem acum că S(1), S(2), …, S(k) sunt toate adevărate, pentru un număr întreg k. Știm că k + 1 este fie un număr prim, fie are factori mai mici decât k + 1. Prin ipoteza noastră, știm că acești factori pot fi scriși ca produs de numere prime. Prin urmare, cu excepția cazului în care este prim, k + 1 poate fi scris, de asemenea, ca un produs de numere prime. Acest lucru înseamnă că S(k + 1) este adevărat.
Prin inducție puternică, S(n) este adevărat pentru toate numerele n mai mari decât 1. ■
Pentru a demonstra că această factorizare primă este unică (cu excepția cazului în care numărați ordonări diferite ale factorilor) este nevoie de mai multă muncă, dar nu este deosebit de greu.
Se pare că principiul inducției slabe și principiul inducției puternice sunt echivalente: fiecare îl implică pe celălalt. De asemenea, amândouă sunt echivalente cu o a treia teoremă, principiul ordonării în bine: orice ansamblu (nevid) de numere naturale are un element minim, mai mic decât toate celelalte.
Principiul ordonării în bine este caracteristica definitorie a numerelor naturale. Este una dintre axiomele de bază folosite pentru a defini numerele naturale ![]() = {1, 2, 3, …}. Aceste axiome se numesc axiomele lui Peano, după numele matematicianului italian Guiseppe Peano (1858 – 1932).
= {1, 2, 3, …}. Aceste axiome se numesc axiomele lui Peano, după numele matematicianului italian Guiseppe Peano (1858 – 1932).
Proba prin contradicție
Proba prin contradicție este o altă tehnică importantă de demonstrație. Dacă vrem să demonstrăm un enunț S, presupunem că S nu era adevărat. Folosind această presupunere, încercăm să deducem un rezultat fals, cum ar fi 0 = 1. Dacă toți pașii noștri au fost corecți și rezultatul este fals, presupunerea noastră inițială trebuie să fi fost greșită. Presupunerea noastră inițială a fost că S nu este adevărat, ceea ce înseamnă că S este de fapt adevărat.
Această tehnică poate fi folosită în multe circumstanțe diferite, cum ar fi demonstrarea faptului că √2 este irațional, demonstrarea faptului că numerele reale sunt nenumărabile sau demonstrarea faptului că există o infinitate de numere prime.
Iată un alt exemplu amuzant:
Potem folosi dovada prin contradicție, împreună cu principiul ordonării bine ordonate, pentru a dovedi că toate numerele naturale sunt „interesante”.
Să presupunem că nu toate numerele naturale sunt interesante și fie S ansamblul numerelor neinteresante. Prin principiul ordonării bine, S are un cel mai mic membru x care este cel mai mic număr neinteresant. Această proprietate curioasă face în mod clar din x un număr deosebit de interesant. Aceasta este o contradicție deoarece am presupus că x este neinteresant.
Din acest motiv toate numerele sunt interesante. ■
Gödel și teoremele neprobabile

Kurt Gödel (1906-1978)
La începutul secolului XX, matematica a început să se dezvolte rapid, cu mii de matematicieni care lucrau în nenumărate domenii noi. David Hilbert (1862 – 1943) a pus la punct un program amplu de formalizare a matematicii și de rezolvare a oricăror inconsecvențe din fundamentele matematicii. Acesta includea demonstrarea tuturor teoremelor folosind un set de axiome simple și universale, dovedirea faptului că acest set de axiome este consecvent și demonstrarea faptului că acest set de axiome este complet, adică că orice afirmație matematică poate fi demonstrată sau infirmată folosind axiomele.
Din păcate, aceste planuri au fost distruse de Kurt Gödel în 1931. El a demonstrat că în orice sistem matematic (suficient de complex) cu un anumit set de axiome, se pot găsi unele enunțuri care nu pot fi nici dovedite, nici infirmate folosind acele axiome. De asemenea, nu este posibil să se dovedească faptul că un anumit set de axiome este consecvent, folosind nimic altceva decât axiomele în sine.
Descoperirea lui Gödel se bazează pe faptul că un set de axiome nu poate fi folosit pentru a spune ceva despre el însuși, cum ar fi dacă este consecvent sau nu. Probleme cu autoreferința pot fi găsite nu numai în matematică, ci și în limbaj. Iată Paradoxul mincinosului:
„Această propoziție este falsă.”
Propoziția de mai sus încearcă să spună ceva despre ea însăși. Dacă este adevărată, atunci propoziția ne spune că este falsă. Dacă este falsă, atunci propoziția ne spune că nu este falsă, adică că este adevărată. De fapt, propoziția nu este nici adevărată, nici falsă.
Când a fost publicată pentru prima dată, teoremele lui Gödel au fost profund tulburătoare pentru mulți matematicieni. Atunci când vă propuneți să demonstrați o observație, nu știți dacă există o demonstrație – rezultatul ar putea fi adevărat, dar imposibil de demonstrat. Astăzi știm că incompletitudinea este o parte fundamentală nu numai a logicii, ci și a informaticii, care se bazează pe mașini care efectuează operații logice.
În mod surprinzător, este posibil să se demonstreze că anumite afirmații sunt imposibil de demonstrat. Un exemplu este Ipoteza Continuumului, care se referă la dimensiunea seturilor infinite.
Caută spre sfârșitul vieții sale, Kurt Gödel a dezvoltat probleme mintale grave și a murit de autoinfuzie în 1978. Ideile sale despre fundamentele logicii au fost cele mai profunde de la dezvoltarea demonstrației de către grecii antici.
.