
Bertrand Russell (1872-1970) și A.N. Whitehead (1861-1947)
Bertrand Russell și Alfred North Whitehead au fost matematicieni, logicieni și filosofi britanici, care s-au aflat în avangarda revoltei britanice împotriva idealismului continental la începutul secolului al XX-lea și, împreună, au adus contribuții importante în domeniul logicii matematice și al teoriei seturilor.
Whitehead a fost cel mai în vârstă dintre cei doi și provenea mai degrabă din domeniul matematicii pure. El a devenit tutorele lui Russell la Trinity College, Cambridge, în anii 1890, și apoi a colaborat cu fostul său student mai celebru în primul deceniu al secolului XX la lucrarea lor monumentală, „Principia Mathematica”. Cu toate acestea, după Primul Război Mondial, pe care Russell l-a petrecut în mare parte în închisoare din cauza activităților sale pacifiste, colaborarea a încetat, iar cariera academică a lui Whitehead a rămas mereu în umbra celei a mult mai flamboaiantei Russell. A emigrat în Statele Unite în anii 1920, unde și-a petrecut restul vieții.
Russell s-a născut într-o familie bogată din aristocrația britanică, deși părinții săi erau extrem de liberali și radicali pentru acele vremuri. Părinții săi au murit când Russell era destul de tânăr, iar el a fost crescut în mare parte de bunica sa, de factură ferm victoriană (deși destul de progresistă). Adolescența sa a fost foarte singuratică și a suferit de crize de depresie, afirmând mai târziu că doar dragostea sa pentru matematică l-a împiedicat să se sinucidă. A studiat matematică și filozofie la Universitatea Cambridge cu G.E. Moore și A.N. Whitehead, unde a devenit un filozof inovator, un scriitor prolific pe mai multe teme, un ateu convins și un matematician și logician inspirat. Astăzi, este considerat unul dintre fondatorii filosofiei analitice, dar a scris despre aproape toate domeniile majore ale filosofiei, în special metafizică, etică, epistemologie, filosofia matematicii și filosofia limbajului.
Russell a fost un activist politic angajat și de profil înalt de-a lungul vieții sale îndelungate. A fost un proeminent activist anti-război atât în timpul Primului cât și al celui de-al Doilea Război Mondial, a susținut comerțul liber și anti-imperialismul, iar mai târziu a devenit un militant strident pentru dezarmarea nucleară și socialism, precum și împotriva lui Adolf Hitler, a totalitarismului sovietic și a implicării SUA în războiul din Vietnam.
Paradoxul lui Russell
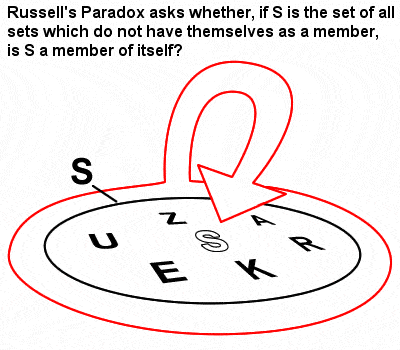
Paradoxul lui Russell
Matematica lui Russell a fost foarte mult influențată de teoria seturilor și de logicismul pe care Gottlob Frege le-a dezvoltat în urma primelor lucrări revoluționare ale lui Cantor asupra seturilor. Cu toate acestea, în lucrarea sa „Principiile matematicii” din 1903, el a identificat ceea ce a ajuns să fie cunoscut sub numele de Paradoxul lui Russell (un set care conține seturi care nu sunt membre ale lui însuși), care a arătat că teoria naivă a seturilor a lui Frege ar putea duce, de fapt, la contradicții.
Paradoxul este ilustrat uneori prin acest exemplu simplist: „Dacă un frizer îi bărbierește pe toți și numai pe acei oameni din sat care nu se bărbieresc singuri, se bărbierește el însuși?”
Paradoxul părea să implice faptul că nu se mai poate avea încredere în înseși fundamentele întregii matematici și că, chiar și în matematică, adevărul nu poate fi niciodată cunoscut în mod absolut (lucrările ulterioare ale lui Gödel și Turing nu vor face decât să înrăutățească situația). Critica lui Russell a fost suficientă pentru a zdruncina încrederea lui Frege în întregul edificiu al logicismului, iar el a fost suficient de amabil să recunoască acest lucru în mod deschis într-un apendice scris în grabă la volumul II al „Legilor de bază ale aritmeticii” sale.
Dar magnum opus-ul lui Russell a fost monolitul „Principia Mathematica”, publicat în trei volume în 1910, 1912 și 1913. Primul volum a fost scris în colaborare cu Whitehead, deși ultimele două au fost aproape în întregime opera lui Russell. Aspirația acestei lucrări ambițioase nu era nimic mai puțin decât o încercare de a deriva întreaga matematică din axiome pur logice, evitând în același timp tipurile de paradoxuri și contradicții întâlnite în lucrările anterioare ale lui Frege privind teoria seturilor. Russell a realizat acest lucru prin utilizarea unei teorii sau a unui sistem de „tipuri”, prin care fiecărei entități matematice îi este atribuit un tip în cadrul unei ierarhii de tipuri, astfel încât obiectele de un anumit tip să fie construite exclusiv din obiecte de tipuri precedente mai jos în ierarhie, evitându-se astfel buclele. Fiecare set de elemente este, așadar, de un tip diferit de fiecare dintre elementele sale, astfel încât nu se poate vorbi de „setul tuturor seturilor” și de construcții similare, care conduc la paradoxuri.
Cu toate acestea, „Principia” cerea, pe lângă axiomele de bază ale teoriei tipurilor, încă trei axiome care păreau a nu fi adevărate ca simple chestiuni de logică, și anume „axioma infinitului” (care garantează existența a cel puțin un ansamblu infinit, și anume ansamblul tuturor numerelor naturale), „axioma alegerii” (care asigură că, dată fiind orice colecție de „pubele”, fiecare conținând cel puțin un obiect, este posibil să se facă o selecție de exact un obiect din fiecare coș, chiar dacă există un număr infinit de coșuri, și că nu există nicio „regulă” pentru ce obiect să se aleagă din fiecare) și „axioma reductibilității” a lui Russell (care afirmă că orice funcție de adevăr propozițională poate fi exprimată printr-o funcție de adevăr predicativă echivalentă din punct de vedere formal).
În timpul celor aproximativ zece ani pe care Russell și Whitehead i-au petrecut la „Principia”, proiecte după proiecte au fost începute și abandonate pe măsură ce Russell își regândea constant premisele de bază. Russell și soția sa, Alys, s-au mutat chiar la Whitehead pentru a grăbi lucrările, deși propria sa căsnicie a avut de suferit deoarece Russell s-a îndrăgostit de tânăra soție a lui Whitehead, Evelyn. În cele din urmă, Whitehead a insistat asupra publicării lucrării, chiar dacă aceasta nu era (și s-ar putea să nu fie niciodată) completă, deși au fost nevoiți să o publice pe cheltuiala lor, deoarece nicio editură comercială nu s-a atins de ea.
Principia Mathematica

O mică parte din lunga demonstrație că 1+1 =2 din „Principia Mathematica”
Oareceva idee despre amploarea și cuprinderea „Principia” poate fi desprinsă din faptul că este nevoie de peste 360 de pagini pentru a demonstra definitiv că 1 + 1 = 2.
Astăzi, este considerată pe scară largă ca fiind una dintre cele mai importante și fundamentale lucrări de logică de la „Organon” lui Aristotel încoace. A părut remarcabil de reușită și de rezistentă în scopurile sale ambițioase și, în curând, a câștigat faima mondială pentru Russell și Whitehead. Într-adevăr, doar teorema de incompletitudine a lui Gödel din 1931 a demonstrat în cele din urmă că „Principia” nu putea fi atât consecventă, cât și completă.
Russell a fost decorat cu Ordinul de Merit în 1949 și cu Premiul Nobel pentru Literatură în anul următor. Faima sa a continuat să crească, chiar și în afara cercurilor academice, și a devenit un fel de nume cunoscut mai târziu, deși în mare parte ca urmare a contribuțiilor sale filosofice și a activismului său politic și social, pe care l-a continuat până la sfârșitul lungii sale vieți. A murit de gripă în iubitul său Țară Galilor, la marea vârstă de 97 de ani.
| << Înapoi la Hardy și Ramanujan | Înapoi la Hilbert >> |