Spiralele arhimedice sunt adesea utilizate în analiza bobinelor inductoare, a schimbătoarelor de căldură spiralate și a dispozitivelor microfluidice. Astăzi, vom demonstra cum să construim o spirală Archimedeană folosind ecuații analitice și derivatele lor pentru a defini un set de curbe spirale. Pe baza acestor curbe, vom crea apoi o geometrie 2D cu o grosime specifică, extrudând-o până la o geometrie 3D completă.
O scurtă introducere în spiralele arhimediene
Observate pe scară largă în natură, spiralele, sau elicele, sunt utilizate în multe proiecte de inginerie. Ca inginer electrician, de exemplu, puteți înfășura bobine inductive în modele spiralate și proiecta antene elicoidale. În calitate de inginer mecanic, puteți utiliza spiralele la proiectarea arcurilor, a angrenajelor elicoidale sau chiar a mecanismului de ceas evidențiat mai jos.

Un exemplu de spirală arhimedică utilizată într-un mecanism de ceas. Imagine realizată de Greubel Forsey. Licențiat prin CC BY-SA 3.0, via Wikimedia Commons.
Aici, ne vom concentra asupra unui tip specific de spirală, cel care este prezentat în mecanismul prezentat mai sus: o spirală arhimedeană. O spirală arhimedeană este un tip de spirală care are o distanță fixă între spirele sale succesive. Această proprietate îi permite să fie utilizată pe scară largă în proiectarea bobinelor plate și a arcurilor.
Potem descrie o spirală arhimedeană cu următoarea ecuație în coordonate polare:
unde a și b sunt parametrii care definesc raza inițială a spiralei și distanța dintre spirele sale succesive, cea din urmă fiind egală cu 2 \pi b. Rețineți că o spirală arhimedeană este, de asemenea, denumită uneori și spirală aritmetică. Acest nume provine de la progresia aritmetică a distanței de la origine până la un punct de pe aceeași radială.
Designing a Parameterized Archimedean Spiral Geometry
Acum că am introdus spiralele arhimediene, să aruncăm o privire asupra modului de a parametriza și de a crea un astfel de design pentru analiză în COMSOL Multiphysics.
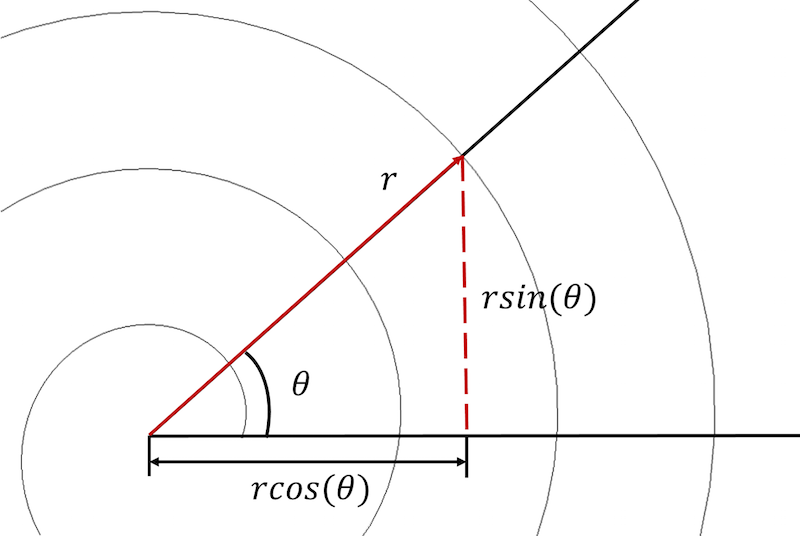
O spirală arhimedică poate fi descrisă atât în coordonate polare, cât și în coordonate carteziene.
Pentru a începe, trebuie să convertim ecuațiile spiralei dintr-un sistem de coordonate polare într-un sistem de coordonate carteziene și să exprimăm fiecare ecuație într-o formă parametrică:
x_{componenta}=rcos(\theta) \\
y_{componenta}=rsin(\theta)
\end{align*}
Această transformare ne permite să rescriem ecuația spiralei arhimediene într-o formă parametrică în sistemul de coordonate carteziene:
x_{componenta}=(a+b\theta)cos(\theta) \\
y_{componenta}=(a+b\theta)sin(\theta)
\end{align*}
În COMSOL Multiphysics, este necesar să se decidă asupra setului de parametri care vor defini geometria spiralei. Acești parametri sunt raza inițială a spiralei a_{initial}, raza finală a spiralei a_{final} și numărul dorit de spire n. Rata de creștere a spiralei b poate fi exprimată astfel:
În continuare, trebuie să stabilim unghiul de început al spiralei theta_0 și unghiul final theta_f. Să începem cu valorile theta_0=0 și theta_f=2 \pi n. Cu aceste informații, suntem capabili să definim un set de parametri pentru geometria spiralei.
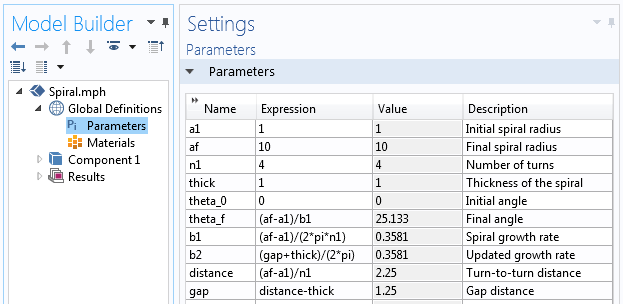
Parametrii utilizați pentru a construi geometria spiralei.
Pentru a construi această spirală, vom începe cu o componentă 3D și vom crea un plan de lucru în ramura Geometry. În geometria Work Plane, adăugăm apoi o Curbă parametrică și folosim ecuațiile parametrice menționate mai sus cu un unghi variabil pentru a desena o versiune 2D a spiralei arhimediene. Aceste ecuații pot fi introduse direct în câmpul Expression (Expresie) al curbei parametrice sau putem defini mai întâi fiecare ecuație într-o nouă funcție Analytic (Analitică) sub forma:
X_{fun}=(a+bs)cos(s) \
Y_{fun}=(a+bs)sin(s) \
\end{align*}
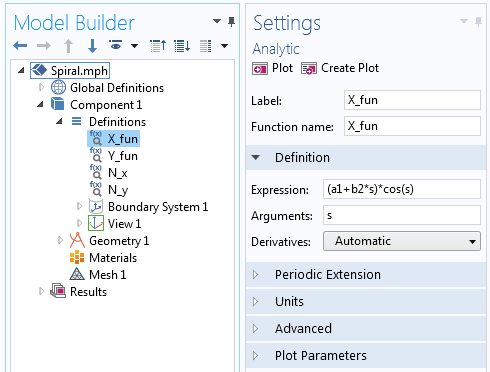
Componenta X a ecuației spiralei arhimediene definită în funcția analitică.
Funcția analitică poate fi utilizată în expresiile pentru curba parametrică. În această Curbă Parametrică, variem parametrul s de la unghiul inițial al spiralei, theta_0, până la unghiul final al spiralei, theta_f=2 \pi n.
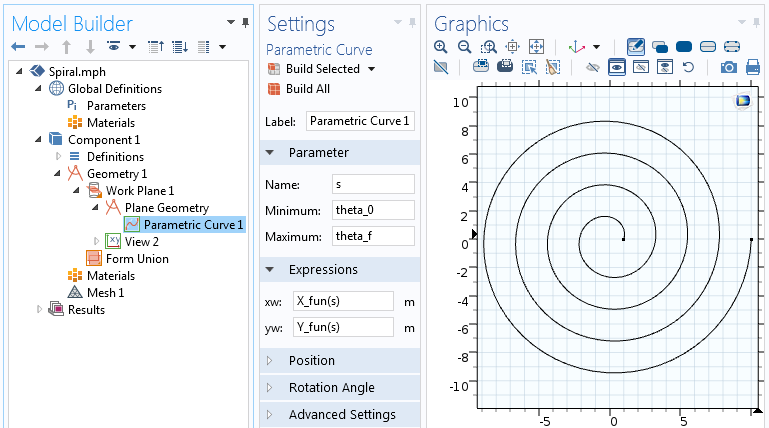
Setările pentru funcția Curbă Parametrică.
Ecuațiile spiralei parametrice utilizate în funcția Curbă Parametrică vor avea ca rezultat o spirală reprezentată de o curbă. Să ne bazăm acum pe această geometrie, adăugându-i grosime pentru a crea un obiect solid 2D.
Până în acest moment, spirala noastră a fost parametrizată în termeni de rază inițială a_{initial}, rază finală a_{final} și numărul dorit de spire n. Acum, trebuie să încorporăm grosimea ca un alt parametru de control în ecuația spiralei.
Să începem cu proprietatea principală a spiralei, care afirmă că distanța dintre spirele spiralei este egală cu 2 \pi b. Aceasta este, de asemenea, echivalentă cu \frac{a_{final}-a_{initial}}{n}. Pentru a încorpora grosimea, reprezentăm distanța dintre fiecare spire succesivă a spiralei ca o sumă a grosimii spiralei și a distanței rămase între spire, thick+gap.
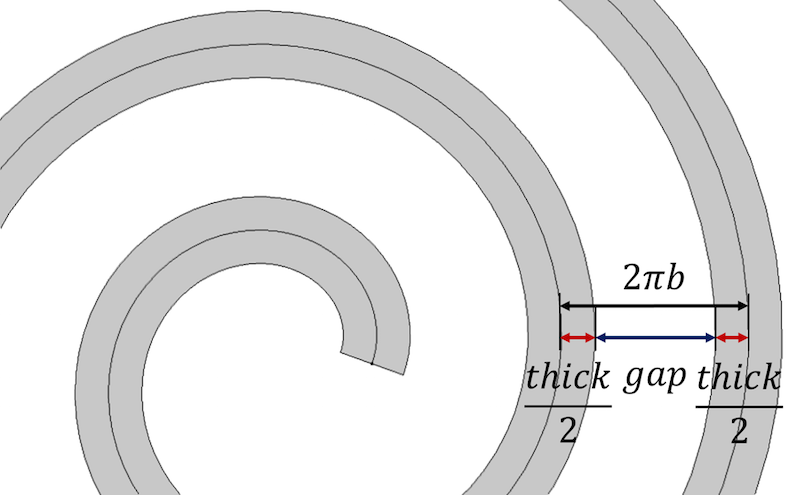
Distanța dintre spirele spiralei este definită în funcție de parametrii grosime și distanța dintre spire.
Pentru a controla grosimea și a obține o distanță identică între spire, distanța poate fi exprimată astfel:
distanța=\frac{a_{initial}-a_{final}}}{n} \\
gap=distanța-grosime
\end{align*}
După definirea grosimii și exprimarea distanței dintre spire în funcție de grosime și de distanța constantă dintre liniile centrale ale spiralei, putem rescrie parametrul de creștere a spiralei în funcție de grosime sub forma:
distance=2\pi b \\
b=\frac{gap+thick}{2\pi}
\end{align*}
Vom dori, de asemenea, să exprimăm unghiul final al spiralei în termeni de raze inițiale și finale:
\theta_{final}=2 \pi n \\
a_{final}=\text{distanța totală}+a_{initial} \\
a_{final}=2 \pi bn+a_{initial} \\
n=\frac{a_{final}-a_{initial}}{2 \pi b} \
\theta_{final}=\frac{2 \pi (a_{final}-a_{initial})}{2 \pi b} \
\theta_{final}=\frac{a_{final}-a_{initial}}{b}{b}
\end{align*}
Vreți să începeți spirala de la un alt unghi decât zero? Dacă da, va trebui să adăugați acest unghi inițial la unghiul final în expresia pentru parametru: theta_f=\frac{a_{final}-a_{initial}}{b}+theta_0.
Duplicarea de două ori a curbei spiralei existente și plasarea acestor curbe cu un decalaj de -\frac{strimă}{2} și +\frac{strimă}{2} față de curba inițială a spiralei ne permite să construim spirala cu grosime. Pentru a poziționa corect spiralele superioare și inferioare, trebuie să ne asigurăm că spiralele decalate sunt normale la curba inițială a spiralei. Acest lucru se poate realiza prin înmulțirea distanței de decalare \pm\frac{stres}{2} cu vectorul unitar normal la curba spiralei. Ecuațiile vectorilor normali la o curbă în formă parametrică sunt:
unde s este parametrul utilizat în caracteristica curbă parametrică. Pentru a obține o normală unitară, trebuie să împărțim aceste expresii la lungimea normalei:
Ecuațiile noastre parametrice actualizate pentru spirala Archimedeană cu o deplasare de jumătate de grosime sunt:
x_{component}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \\
y_{componenta}=(a+bs)sin(s)+\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2}
\end{align*}
Scrierea acestor ecuații în câmpurile de expresie ale curbei parametrice poate consuma destul de mult timp. Ca atare, introducem următoarea notație:
N_x=-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}. \\
N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }}
\end{align*}
unde fiecare N_x și N_y este definit prin intermediul funcției Analytic din COMSOL Multiphysics, similar cu modul în care am definit X_{fun} și Y_{fun} pentru prima curbă parametrică. În cadrul funcției, folosim operatorul de diferențiere, d(f(x),x), pentru a lua derivata, așa cum este ilustrat în următoarea captură de ecran.
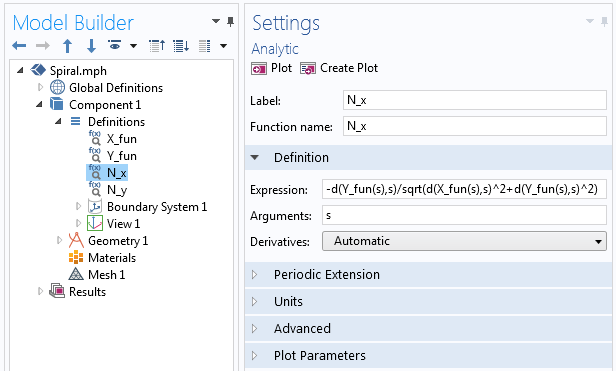
Exemple de operator de derivare utilizat în funcția Analytic.
Funcțiile X_{fun}, Y_{fun}, N_x și N_y pot fi apoi folosite direct în expresiile curbei parametrice pentru curba de pe o parte:
x_{lower}=X_{fun}(s)+N_x(s)\frac{thick}{2} \\
y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2}
\end{align*}
Funcțiile pot fi folosite și pentru curba de pe cealaltă parte:
x_{upper}=X_{fun}(s)-N_x(s)\frac{thick}{2} \\
y_{upper}=Y_{fun}(s)-N_y(s)\frac{thick}{2}
\end{align*}
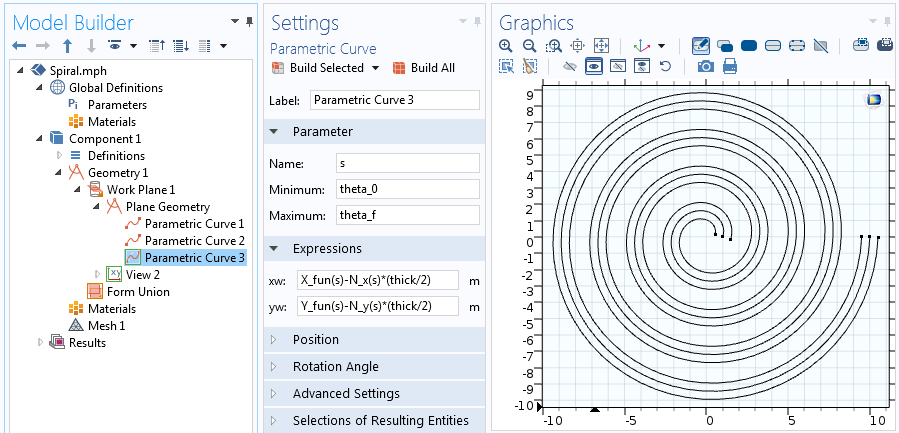
Ecuațiile pentru cea de-a doua dintre cele două curbe parametrice decalate.
Pentru a uni capetele a două curbe, adăugăm încă două curbe parametrice folosind o ușoară modificare a ecuațiilor menționate mai sus. Pentru curba care unește centrul spiralei, trebuie să evaluăm X_{fun}, Y_{fun}, N_x și N_y pentru valoarea inițială a unghiului, theta. Pentru curba care se unește cu partea exterioară a spiralei, trebuie să evaluăm valoarea finală a lui theta. Prin urmare, curba care se unește în centru este:
X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot\frac{thick}{2} \\
Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2}
\end{align*}
Curba de îmbinare exterioară, între timp, este:
X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdot\frac{thick}{2} \\
Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2}
\end{align*}
În ambele ecuații de mai sus, s trece de la -1 la +1, așa cum se arată în captura de ecran de mai jos.
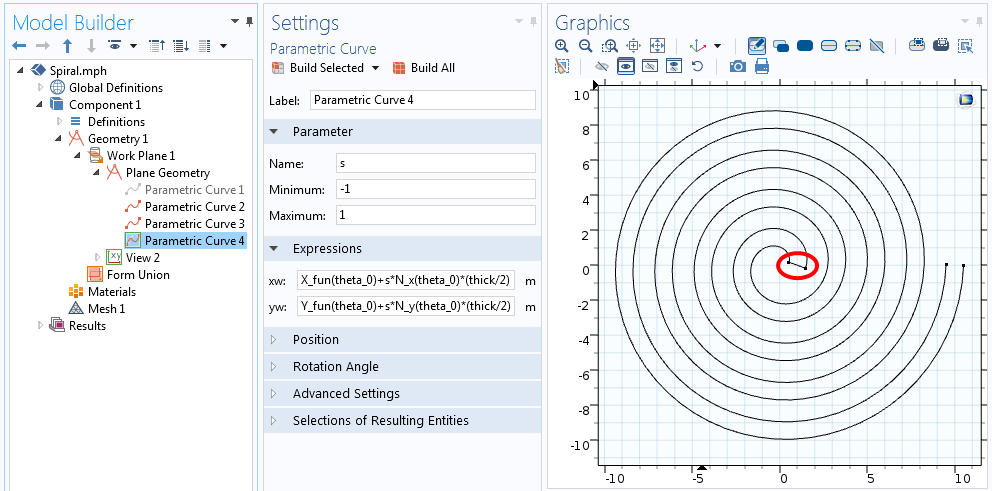
Ecuații pentru curba care unește un capăt al spiralei.
Acum avem cinci curbe care definesc linia centrală a spiralei și toate cele patru laturi ale profilului. Putem dezactiva (sau chiar șterge) curba care descrie linia mediană, deoarece nu este cu adevărat necesară, lăsând doar conturul spiralei. Cu conturul spiralei noastre definit, operația „Convert to Solid” poate fi utilizată pentru a crea un singur obiect geometric. Această spirală 2D poate fi în cele din urmă extrudată în 3D prin intermediul operației Extrude.
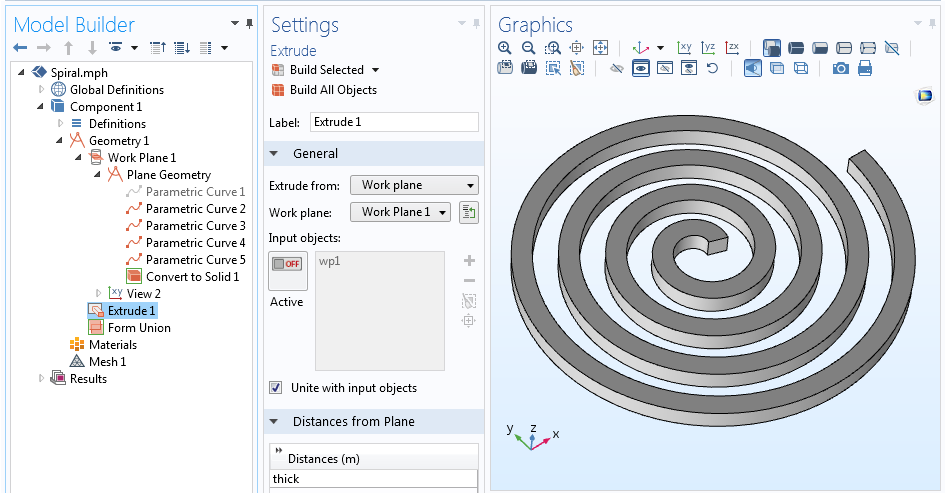
Secvența geometrică completă și geometria spiralei 3D extrudate.
Closing Remarks on Modeling Archimedean Spirals in COMSOL Multiphysics
Am parcurs etapele de creare a unei spirale arhimediene complet parametrizate. Cu această geometrie a spiralei, puteți modifica oricare dintre parametri și experimenta cu diferite modele sau chiar le puteți utiliza ca parametri într-un studiu de optimizare. Vă încurajăm să utilizați această tehnică în propriile dvs. procese de modelare, avansând analiza proiectului dvs. special de inginerie bazat pe spirală.
.