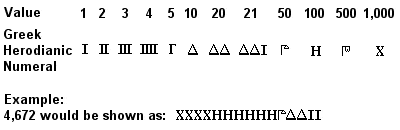
Numerele vechi grecești herodiene
Cum imperiul grec a început să-și extindă sfera de influență în Asia Mică, Mesopotamia și dincolo de ea, grecii au fost suficient de inteligenți pentru a adopta și adapta elemente utile din societățile pe care le-au cucerit. Acest lucru a fost la fel de adevărat și în cazul matematicii lor ca orice altceva, iar ei au adoptat elemente de matematică atât de la babilonieni, cât și de la egipteni. Dar, în curând, au început să aducă contribuții importante pe cont propriu și, pentru prima dată, putem recunoaște contribuțiile individuale. Până în perioada elenistică, grecii au prezidat una dintre cele mai dramatice și mai importante revoluții în gândirea matematică din toate timpurile.
Numerele attice sau erodiene
Sistemul numeric grecesc antic, cunoscut sub numele de numere attice sau erodiene, a fost pe deplin dezvoltat până în jurul anului 450 î.Hr. și a fost folosit în mod regulat probabil încă din secolul al VII-lea î.Hr. Era un sistem de bază 10 asemănător cu cel egiptean anterior (și chiar mai asemănător cu sistemul roman ulterior), cu simboluri pentru 1, 5, 10, 50, 100, 500 și 1.000 repetate de câte ori era nevoie pentru a reprezenta numărul dorit. Adăugarea se făcea prin însumarea separată a simbolurilor (1, 10, 100 etc.) din numerele care trebuiau adăugate, iar înmulțirea era un proces laborios bazat pe dublări succesive (împărțirea se baza pe inversul acestui proces).
Teorema de interceptare a lui Thales
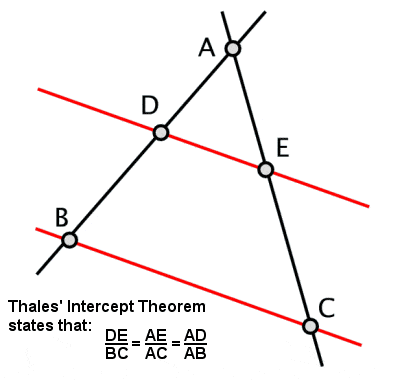
Teorema de interceptare a lui Thales
Dar cea mai mare parte a matematicii grecești era bazată pe geometrie. Thales, unul dintre cei Șapte Înțelepți ai Greciei Antice, care a trăit pe coasta ionică a Asiei Mici în prima jumătate a secolului al VI-lea î.Hr., este considerat de obicei ca fiind primul care a stabilit liniile directoare pentru dezvoltarea abstractă a geometriei, deși ceea ce cunoaștem din lucrările sale (cum ar fi cele privind triunghiurile similare și dreptunghice) pare acum destul de elementar.
Thales a stabilit ceea ce a devenit cunoscut sub numele de Teorema lui Thales, conform căreia dacă un triunghi este desenat în interiorul unui cerc cu latura lungă ca un diametru al cercului, atunci unghiul opus va fi întotdeauna un unghi drept (precum și alte câteva proprietăți conexe derivate din aceasta). Lui i se atribuie, de asemenea, o altă teoremă, cunoscută și sub numele de Teorema lui Thales sau Teorema de interceptare, despre raporturile segmentelor de dreaptă care se creează dacă două drepte care se intersectează sunt interceptate de o pereche de paralele (și, prin extensie, raporturile laturilor triunghiurilor similare).
Într-o oarecare măsură, totuși, legenda matematicianului Pitagora din Samos din secolul al VI-lea î.Hr. a devenit sinonimă cu nașterea matematicii grecești. Într-adevăr, se crede că el ar fi inventat atât cuvintele „filozofie” („iubirea de înțelepciune”), cât și „matematică” („ceea ce se învață”). Pitagora a fost probabil primul care și-a dat seama că se poate construi un sistem complet de matematică, în care elementele geometrice să corespundă cu numere. Teorema lui Pitagora (sau Teorema lui Pitagora) este una dintre cele mai cunoscute dintre toate teoremele matematice. Dar el rămâne o figură controversată, după cum vom vedea, iar matematica greacă nu s-a limitat în niciun caz la un singur om.
Trei probleme geometrice
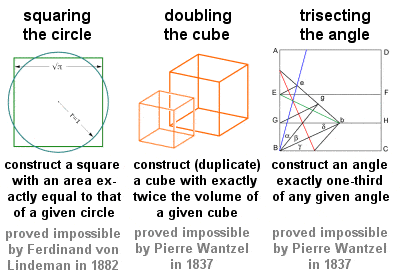
Cele trei probleme clasice
Trei probleme geometrice în special, adesea denumite cele trei probleme clasice, și toate trebuind să fie rezolvate prin mijloace pur geometrice, folosind doar o muchie dreaptă și un compas, datează din primele zile ale geometriei grecești: „ridicarea la pătrat (sau cuadratură) a cercului”, „dublarea (sau duplicarea) cubului” și „trisecția unui unghi”. Aceste probleme intransigente au avut o influență profundă asupra geometriei viitoare și au dus la multe descoperiri fructuoase, deși soluțiile lor efective (sau, după cum s-a dovedit, dovezile imposibilității lor) au trebuit să aștepte până în secolul al XIX-lea.
Hippocrate din Chios (a nu se confunda cu marele medic grec Hipocrate din Kos. O biografie detaliată aici.) a fost un astfel de matematician grec care s-a aplicat la aceste probleme în secolul al V-lea î.Hr. (contribuția sa la problema „pătratului cercului” este cunoscută sub numele de Lunele lui Hipocrate). Influenta sa carte „Elementele”, care datează din jurul anului 440 î.Hr., a fost prima compilație a elementelor de geometrie, iar lucrarea sa a fost o sursă importantă pentru lucrările ulterioare ale lui Euclid.
Paradoxul lui Zenon despre Ahile și broasca țestoasă
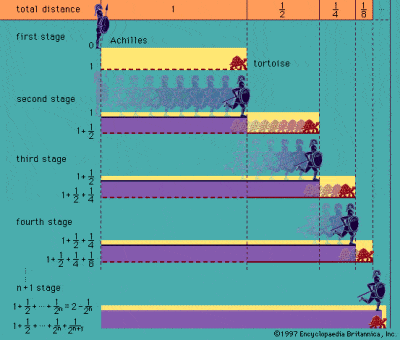
Paradoxul lui Zenon despre Ahile și broasca țestoasă
Grecii au fost primii care s-au confruntat cu ideea de infinit, așa cum este descrisă în binecunoscutele paradoxuri atribuite filosofului Zenon din Elea în secolul al V-lea î.Hr. Cel mai faimos dintre paradoxurile sale este cel al lui Ahile și țestoasa, care descrie o cursă teoretică între Ahile și o țestoasă. Ahile îi dă un avans țestoasei mult mai lente, dar în momentul în care Ahile ajunge la punctul de plecare al țestoasei, aceasta din urmă a avansat deja. În momentul în care Ahile ajunge în acel punct, țestoasa a avansat din nou, etc, etc, astfel încât, în principiu, rapidul Ahile nu poate ajunge niciodată din urmă țestoasa lentă.
Paradoxuri precum acesta și așa-numitul Paradox al dicotomiei lui Zenon se bazează pe divizibilitatea infinită a spațiului și timpului și se bazează pe ideea că o jumătate plus un sfert plus o optime plus o șaisprezecime, etc, etc, etc, la infinit nu vor fi niciodată egale cu un întreg. Paradoxul provine însă din presupunerea falsă că este imposibil să se completeze un număr infinit de liniuțe discrete într-un timp finit, deși este extrem de dificil să se demonstreze definitiv această eroare. Grecul antic Aristotel a fost primul dintre cei mulți care au încercat să dezmintă paradoxurile, mai ales că el credea cu tărie că infinitul poate fi doar potențial și nu real.
Democritus, cel mai faimos pentru ideile sale prevăzătoare despre faptul că toată materia este compusă din atomi minusculi, a fost, de asemenea, un pionier al matematicii și geometriei în secolele V – IV î.Hr. și a realizat lucrări cu titluri precum „Despre numere”, „Despre geometrie”, „Despre tangențe”, „Despre cartografiere” și „Despre iraționale”, deși aceste lucrări nu au supraviețuit. Știm însă că a fost printre primii care au observat că un con (sau o piramidă) are o treime din volumul unui cilindru (sau al unei prisme) cu aceeași bază și înălțime și este probabil primul care a luat în considerare în mod serios împărțirea obiectelor într-un număr infinit de secțiuni transversale.
Cu toate acestea, este cu siguranță adevărat că Pitagora, în special, i-a influențat foarte mult pe cei care au venit după el, inclusiv pe Platon, care și-a înființat faimoasa Academie în Atena în 387 î.Hr. și pe protejatul său Aristotel, a cărui lucrare despre logică a fost considerată definitivă timp de peste două mii de ani. Matematicianul Platon este cel mai bine cunoscut pentru descrierea celor cinci solide platonice, dar valoarea operei sale ca profesor și popularizator al matematicii nu poate fi supraestimată.
Eudoxus din Cnidus, elevul lui Platon, este de obicei creditat cu prima punere în aplicare a „metodei epuizării” (dezvoltată ulterior de Arhimede), o metodă timpurie de integrare prin aproximări succesive pe care a folosit-o pentru calcularea volumului piramidei și al conului. De asemenea, a elaborat o teorie generală a proporțiilor, care se aplica atât mărimilor incomensurabile (iraționale) care nu pot fi exprimate ca raport între două numere întregi, cât și mărimilor comensurabile (raționale), extinzând astfel ideile incomplete ale lui Pitagora.
Poate cea mai importantă contribuție unică a grecilor, totuși – și Pitagora, Platon și Aristotel au fost cu toții influenți în această privință – a fost ideea de demonstrație și metoda deductivă de utilizare a pașilor logici pentru a demonstra sau infirma teoreme pornind de la axiomele presupuse inițial. Culturile mai vechi, precum egiptenii și babilonienii, se bazau pe raționamentul inductiv, adică pe utilizarea observațiilor repetate pentru a stabili reguli empirice. Acest concept de demonstrație este cel care conferă matematicii puterea sa și asigură faptul că teoriile dovedite sunt la fel de adevărate astăzi ca și acum două mii de ani și care a pus bazele abordării sistematice a matematicii lui Euclid și a celor care au venit după el.
| << Înapoi la Matematica egipteană | Înapoi la Pitagora >> |
.