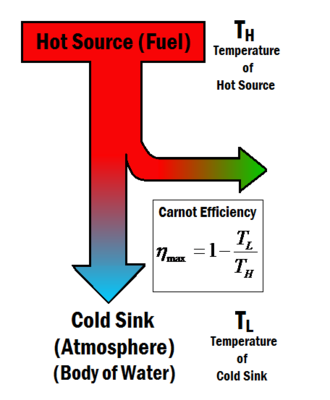
Figura 1: O sursă caldă furnizează energia necesară pentru a produce lucru într-un proces termodinamic. Randamentul Carnot depinde numai de temperatura sursei calde și a radiatorului rece.
Eficiența lui Carnot descrie randamentul termic maxim pe care îl poate atinge un motor termic, așa cum este permis de a doua lege a termodinamicii. Legea a fost derivată de Sadi Carnot în 1824. Carnot a reflectat asupra ideii de randament maxim al unui motor termic, întrebându-se dacă randamentul unui motor termic se poate apropia de 100% sau dacă există o limită superioară care nu poate fi depășită? Răspunsul s-a dovedit a fi că există o valoare maximă, iar Carnot a dezvoltat un motor ideal care, teoretic, ar oferi această eficiență, cunoscut sub numele de motor Carnot. Randamentul maxim, cunoscut sub numele de randamentul Carnot , depinde doar de temperaturile sursei calde și a radiatorului rece și , așa cum se arată în figura 1, și este dat de ecuația de mai jos
(1)
Cea de-a doua lege cere ca căldura reziduală să fie produsă într-un proces termodinamic în care lucrul este efectuat de o sursă de căldură. Un astfel de proces este dat de ecuația
(2)
Cu un randament termic de
(3)
Un astfel de proces este dat de ecuația
(2)
Cu:
- este căldura furnizată sistemului de la un combustibil
- este căldura cedată de sistem către radiatorul rece, cunoscută sub numele de căldură reziduală
- este lucrul util realizat de sistem
În consecință, randamentul Carnot oferă o cantitate maximă de lucru care poate fi obținută de orice motor termic. Se poate observa din ecuația 1 că, fie prin creșterea, fie prin scăderea randamentului, acesta poate fi mărit. În mod ideal, s-ar dori, prin urmare, ca temperatura radiatorului să fie egală cu zero absolut, dar se știe că acest lucru este imposibil. În realitate, radiatorul rece este mediul înconjurător al Pământului. Acest lucru înseamnă că radiatorul rece se află la o temperatură de aproximativ 280-300 Kelvin, iar sursele fierbinți provin din arderea combustibililor care ard la o temperatură de aproximativ 1100 Kelvin (deși cercetarea încearcă mereu să ridice această temperatură). Aceste temperaturi dau o valoare a randamentului Carnot de aproximativ.
Motor Carnot
Un motor Carnot este un motor idealizat, care folosește procese care au interacțiuni mecanice și termice reversibile. Aceasta înseamnă că motorul își poate parcurge mișcările și se poate întoarce la starea inițială fără o creștere a entropiei (fără pierdere de energie). Pentru ca motorul să poată reveni la starea sa inițială fără a crește entropia, motorul trebuie să se afle în echilibru termic pe tot parcursul ciclului său. Condițiile pentru ca un astfel de motor să existe sunt:
- Interacțiuni mecanice: nu se pierde energie sub formă de frecare, prin urmare nu există transfer de căldură în timpul acestor procese mecanice (), cunoscut sub numele de proces adiabatic.
- Interacțiuni termice: transferul de căldură este infinit de lent (cunoscut sub numele de cvasi-static). Aceasta înseamnă că diferența de temperatură dintre sistem și căldura de intrare/ieșire este foarte aproape aceeași, ceea ce face ca transferul de căldură să aibă loc într-o perioadă de timp infinită. Aceste schimburi trebuie să se facă prin menținerea constantă a temperaturii interne a sistemului, cunoscut sub numele de proces izotermic.
Un motor care posedă doar aceste proprietăți este cunoscut sub numele de motor Carnot, care este un „motor perfect reversibil” și prezintă randamentul termic maxim () și, dacă funcționează ca un frigider, coeficientul de performanță (). Deși un astfel de motor ar maximiza eficiența, din punct de vedere al eficacității este teribil de nepractic, deoarece procesele sale idealizate necesită foarte mult timp pentru a produce o cantitate semnificativă de muncă. După cum spune Schroeder, „nu vă deranjați să instalați un motor Carnot în mașina dumneavoastră; deși v-ar crește consumul de benzină, ați fi depășit de pietoni”.
Pentru a afla mai multe despre motorul Carnot, vizitați NASA sau hyperphysics.
.