Diagramele bloc sunt alcătuite dintr-un singur bloc sau dintr-o combinație de blocuri. Acestea sunt utilizate pentru a reprezenta sistemele de control în formă picturală.
Elemente de bază ale diagramei bloc
Elementele de bază ale unei diagrame bloc sunt un bloc, punctul de însumare și punctul de decolare. Să luăm în considerare diagrama bloc a unui sistem de control în buclă închisă, așa cum este prezentată în figura următoare, pentru a identifica aceste elemente.
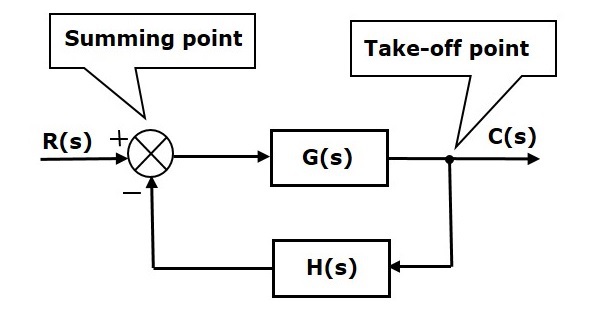
Diagrama bloc de mai sus este formată din două blocuri care au funcțiile de transfer G(s) și H(s). Ea are, de asemenea, un punct de însumare și un punct de decolare. Săgețile indică direcția fluxului de semnale. Să discutăm acum aceste elemente unul câte unul.
Bloc
Funcția de transfer a unei componente este reprezentată de un bloc. Blocul are o singură intrare și o singură ieșire.
Figura următoare prezintă un bloc având intrarea X(s), ieșirea Y(s) și funcția de transfer G(s).

Funcția de transfer,$G(s)=\frac{Y(s)}{X(s)}$
$$\Frecareta din dreapta Y(s)=G(s)X(s)$$
Sursa blocului se obține prin înmulțirea funcției de transfer a blocului cu intrarea.
Punctul de însumare
Punctul de însumare este reprezentat cu un cerc având în interiorul său o cruce (X). Acesta are două sau mai multe intrări și o singură ieșire. El produce suma algebrică a intrărilor. De asemenea, efectuează adunarea sau scăderea sau o combinație de adunare și scădere a intrărilor în funcție de polaritatea intrărilor. Să vedem aceste trei operații una câte una.
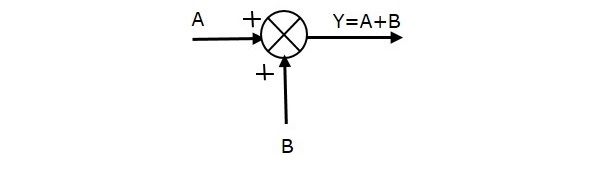
În figura următoare este prezentat punctul de adunare cu două intrări (A, B) și o ieșire (Y). Aici, intrările A și B au un semn pozitiv. Așadar, punctul de adunare produce ieșirea Y ca sumă a lui A și B.
i.e.,Y = A + B.
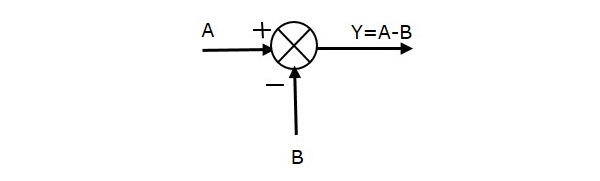
În figura următoare este prezentat punctul de adunare cu două intrări (A, B) și o ieșire (Y). Aici, intrările A și B au semne opuse, adică A are semn pozitiv, iar B are semn negativ. Astfel, punctul de adunare produce ieșirea Y ca diferență între A și B.
Y = A + (-B) = A – B.
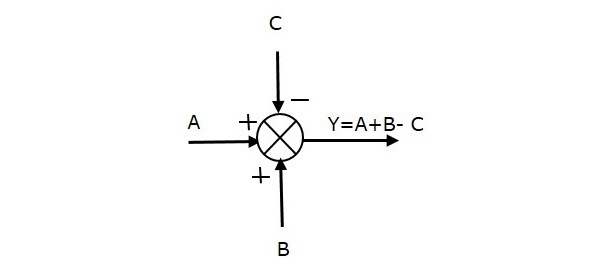
În figura următoare este prezentat punctul de adunare cu trei intrări (A, B, C) și o ieșire (Y). Aici, intrările A și B au semne pozitive, iar C are un semn negativ. Deci, punctul de adunare produce ieșirea Y ca
Y = A + B + (-C) = A + B – C.
Punctul de preluare
Punctul de preluare este un punct din care același semnal de intrare poate trece prin mai mult de o ramură. Aceasta înseamnă că, cu ajutorul punctului de decolare, putem aplica aceeași intrare la unul sau mai multe blocuri, puncte de însumare.
În figura următoare, punctul de decolare este utilizat pentru a conecta aceeași intrare, R(s) la alte două blocuri.
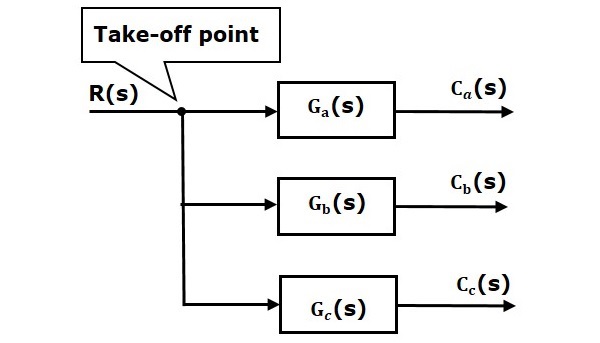
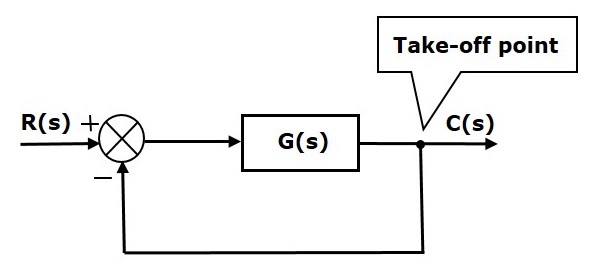
În figura următoare, punctul de decolare este folosit pentru a conecta ieșirea C(s), ca una dintre intrările la punctul de însumare.
Reprezentarea sistemelor electrice prin diagrame bloc
În această secțiune, să reprezentăm un sistem electric cu o diagramă bloc. Sistemele electrice conțin în principal trei elemente de bază – rezistor, inductor și condensator.
Considerăm o serie de circuite RLC, așa cum se arată în figura următoare. Unde, Vi(t) și Vo(t) sunt tensiunile de intrare și de ieșire. Fie i(t) curentul care trece prin circuit. Acest circuit este în domeniul timpului.
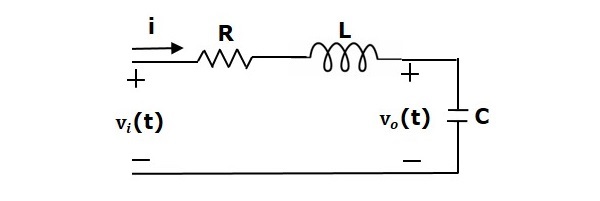
Prin aplicarea transformării Laplace la acest circuit, se va obține circuitul în domeniul s. Circuitul este așa cum se arată în figura următoare.
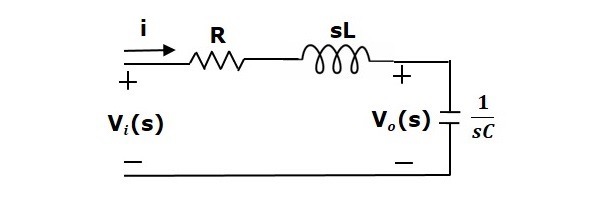
Din circuitul de mai sus, putem scrie
$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$$
$\Frecvența din dreapta I(s)=\stânga \{ \frac{1}{R+sL} \ dreapta \}\left \{ V_i(s)-V_o(s) \ dreapta \}$ (Ecuația 1)
$V_o(s)=\left ( \frac{1}{sC} \ dreapta )I(s)$ (Ecuația 2)
Să desenăm acum diagramele bloc pentru aceste două ecuații în mod individual. Și apoi să combinăm aceste diagrame bloc în mod corespunzător pentru a obține diagrama bloc globală a seriei de circuite RLC (domeniul s).
Ecuația 1 poate fi implementată cu un bloc având funcția de transfer, $\frac{1}{R+sL}$. Intrarea și ieșirea acestui bloc sunt $\left \{ V_i(s)-V_o(s) \right \}}$ și $I(s)$. Avem nevoie de un punct de adunare pentru a obține $\left \{ V_i(s)-V_o(s) \right \}$. Schema bloc a ecuației 1 este prezentată în figura următoare.
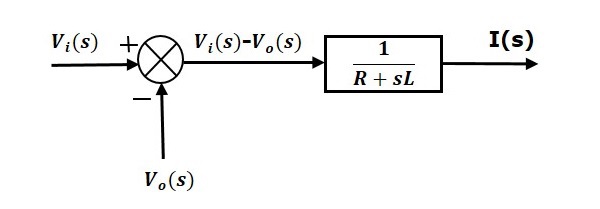
Ecuția 2 poate fi implementată cu un bloc având funcția de transfer, $\frac{1}{sC}$. Intrarea și ieșirea acestui bloc sunt $I(s)$ și $V_o(s)$. Diagrama bloc a ecuației 2 este prezentată în figura următoare.
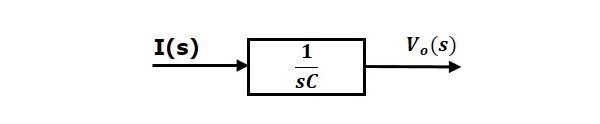
Diagrama bloc globală a seriei de circuite RLC (în domeniul s) este prezentată în figura următoare.
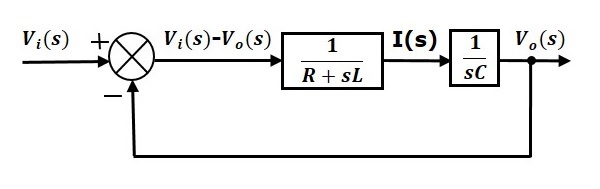
În mod similar, puteți desena diagrama bloc a oricărui circuit sau sistem electric doar urmând această procedură simplă.
-
Convertiți circuitul electric în domeniul timp într-un circuit electric în domeniul s prin aplicarea transformării Laplace.
-
Scrieți ecuațiile pentru curentul care trece prin toate elementele de ramură serie și tensiunea pe toate ramurile de derivație.
-
Desenați diagramele bloc pentru toate ecuațiile de mai sus în mod individual.
-
Combinați corect toate aceste diagrame bloc pentru a obține diagrama bloc globală a circuitului electric (domeniul s).
.