16.3 Strategii mixte
Obiectiv de învățare
- Ce jocuri necesită sau admit aleatorizarea ca parte a soluției lor?
Să luăm din nou în considerare jocul de potrivire a bănuților, așa cum este ilustrat în figura 16.13 „Potrivirea bănuților din nou”.
Figura 16.13 Potrivirea bănuților din nou
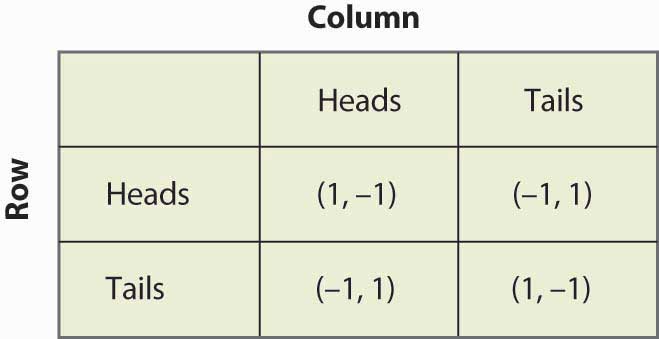
Să presupunem că Rândul crede că Coloana joacă Cap cu probabilitatea p. Atunci, dacă Rândul joacă Cap, Rândul obține 1 cu probabilitatea p și -1 cu probabilitatea (1 – p), pentru o valoare așteptată de 2p – 1. În mod similar, dacă Row joacă Pajură, Row primește -1 cu probabilitatea p (când Column joacă Cap) și 1 cu probabilitatea (1 – p), pentru o valoare așteptată de 1 – 2p. Acest lucru este rezumat în figura 16.14 „Strategie mixtă în potrivirea bănuților”.
Dacă 2p – 1 > 1 – 2p, atunci lui Row îi este mai bine, în medie, să joace Cap decât Pajură. În mod similar, dacă 2p – 1 < 1 – 2p, atunci lui Row îi este mai bine să joace Pajură decât Cap. Dacă, pe de altă parte, 2p – 1 = 1 – 2p, atunci Row primește același câștig indiferent de ceea ce face Row. În acest caz, Row ar putea juca Cap, ar putea juca Pajură sau ar putea să arunce o monedă și să randomizeze jocul lui Row.
Un echilibru Nash cu strategie mixtăUn echilibru Nash în care cel puțin un jucător joacă o strategie randomizată și niciun jucător nu este capabil să își mărească câștigul așteptat jucând o strategie alternativă. presupune că cel puțin un jucător joacă o strategie randomizată și niciun jucător nu este capabil să își mărească câștigul așteptat jucând o strategie alternativă. Un echilibru Nash în care nici un jucător nu randomizează se numește echilibru Nash de strategie purăUn echilibru Nash în care nici un jucător nu randomizează…
Figura 16.14 Strategie mixtă în potrivirea bănuților
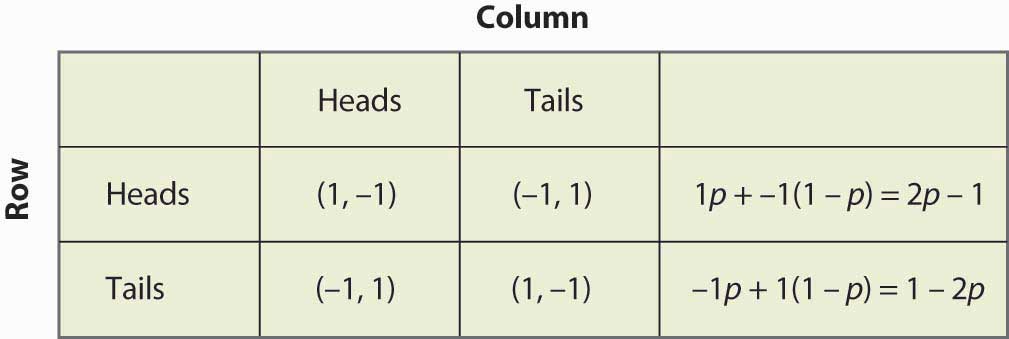
Rețineți că randomizarea necesită egalitatea câștigurilor așteptate. Dacă se presupune că un jucător trebuie să randomizeze pe strategia A sau pe strategia B, atunci ambele strategii trebuie să producă același câștig așteptat. În caz contrar, jucătorul va prefera una dintre ele și nu o va juca pe cealaltă.
Calcularea unei strategii mixte are un element care apare adesea confuz. Să presupunem că Row are de gând să randomizeze. Atunci plățile lui Row trebuie să fie egale pentru toate strategiile pe care Row le joacă cu probabilitate pozitivă. Dar această egalitate în câștigurile lui Row nu determină probabilitățile cu care Row joacă diferitele rânduri. În schimb, această egalitate a remunerațiilor lui Row va determina probabilitățile cu care Column joacă diferitele coloane. Motivul este că probabilitățile coloanei sunt cele care determină câștigurile așteptate pentru Row; dacă Row va juca la întâmplare, atunci probabilitățile coloanei trebuie să fie astfel încât Row să fie dispus să joace la întâmplare.
Așa, de exemplu, am calculat câștigul pentru Row de a juca Cap, care era 2p – 1, unde p era probabilitatea ca Columna să joace Cap. În mod similar, câștigul pentru Rând de a juca Pajură a fost 1 – 2p. Row este dispus să randomizeze dacă acestea sunt egale, ceea ce rezolvă pentru p = ½.
Acum să încercăm un exemplu ceva mai provocator și să revizuim bătălia sexelor. Figura 16.15 „Strategie mixtă în bătălia sexelor” ilustrează din nou plățile.
Figura 16.15 Strategie mixtă în bătălia sexelor
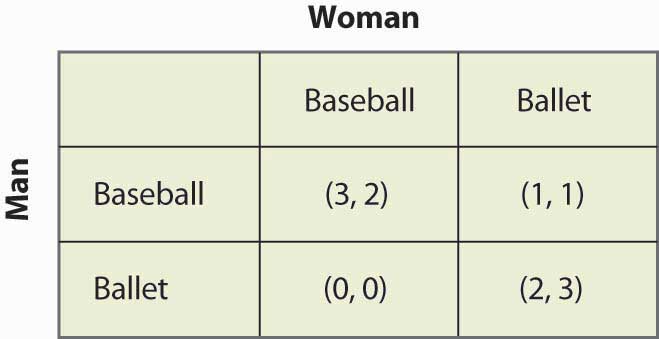
Acest joc are două echilibre Nash de strategie pură: (Baseball, Baseball) și (Balet, Balet). Există o strategie mixtă? Pentru a calcula o strategie mixtă, fie ca Femeia să meargă la jocul Baseball cu probabilitatea p, iar Bărbatul să meargă la jocul Baseball cu probabilitatea q. Figura 16.16 „Calculul complet al strategiei mixte” conține calculul plății strategiei mixte pentru fiecare jucător.
Figura 16.16.16 „Calculul complet al strategiei mixte”.16 Calculul complet al strategiei mixte
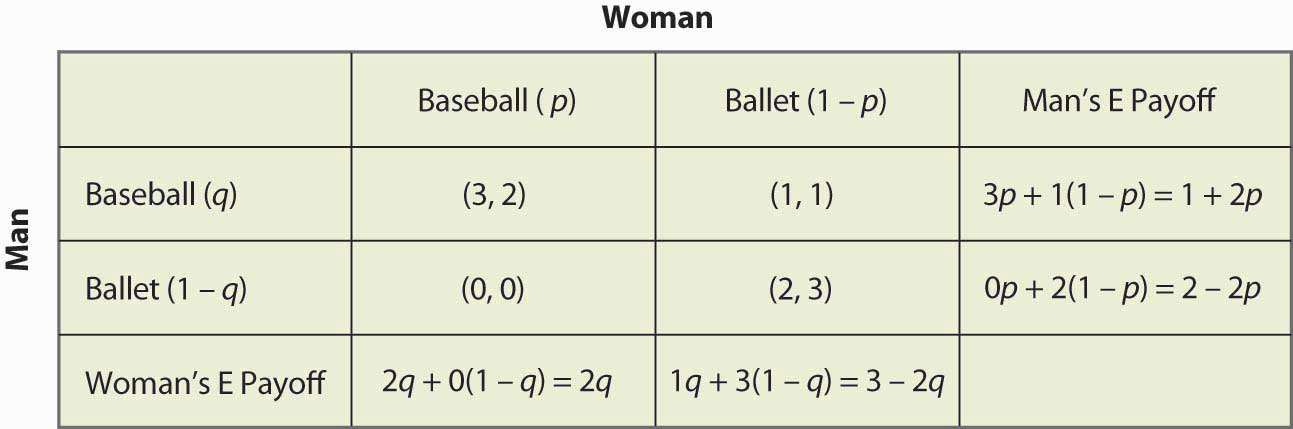
De exemplu, dacă Bărbatul (jucătorul de rând) merge la jocul de baseball, el primește 3 atunci când Femeia merge la jocul de baseball (probabilitatea p), iar în caz contrar primește 1, pentru un câștig așteptat de 3p + 1(1 – p) = 1 + 2p. Celelalte calcule sunt similare, dar ar trebui neapărat să parcurgeți logica și să verificați fiecare calcul.
O strategie mixtă în jocul bătălia sexelor necesită ca ambele părți să randomizeze (deoarece o strategie pură a uneia dintre părți împiedică randomizarea de către cealaltă parte). Indiferența bărbatului între a merge la jocul de baseball și la balet necesită 1 + 2p = 2 – 2p, ceea ce dă p = ¼. Adică, bărbatul va fi dispus să aleagă aleatoriu la ce eveniment participă dacă femeia merge la balet ¾ din timp, iar în caz contrar la meciul de baseball. Acest lucru face ca bărbatul să fie indiferent între cele două evenimente, deoarece el preferă să fie cu femeia, dar îi place să fie și la meciul de baseball. Pentru a compensa avantajul pe care jocul îl deține pentru el, Femeia trebuie să fie mai des la Balet.
În mod similar, pentru ca Femeia să aleagă aleatoriu, Femeia trebuie să obțină câștiguri egale dacă merge la jocul de Baseball și dacă merge la Balet, ceea ce necesită 2q = 3 – 2q, sau q = ¾. Astfel, probabilitatea ca bărbatul să meargă la meciul de baseball este de ¾, iar el merge la balet ¼ din timp. Acestea sunt probabilități independente, astfel încât, pentru a obține probabilitatea ca amândoi să meargă la meciul de baseball, trebuie să înmulțim probabilitățile, ceea ce dă 3/16. Figura 16.17 „Probabilități strategie mixtă” completează probabilitățile pentru toate cele patru rezultate posibile.
Figura 16.17 Probabilități strategie mixtă
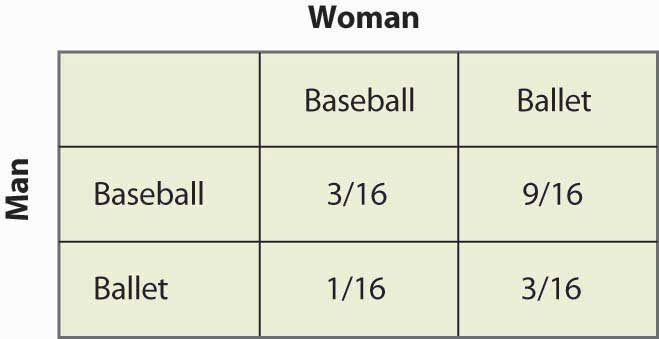
Rețineți că mai mult de jumătate din timp (Baseball, Balet) este rezultatul strategiei mixte, iar cele două persoane nu sunt împreună. Această lipsă de coordonare este, în general, o caracteristică a echilibrelor de strategie mixtă. Plățile așteptate pentru ambii jucători sunt, de asemenea, ușor de calculat. Câștigul bărbatului este 1 + 2p = 2 – 2p și, deoarece p = ¼, bărbatul obține 1½. Un calcul similar arată că câștigul femeii este același. Prin urmare, ambii au rezultate mai proaste decât coordonarea în ceea ce privește rezultatul lor cel mai puțin preferat. Dar acest echilibru Nash de strategie mixtă, oricât de nedorit ar părea, este un echilibru Nash în sensul că niciuna dintre părți nu-și poate îmbunătăți propriul câștig, având în vedere comportamentul celeilalte părți.
În bătălia sexelor, echilibrul Nash de strategie mixtă poate părea puțin probabil; și ne-am putea aștepta ca cuplul să se coordoneze mai eficient. Într-adevăr, un simplu apel la telefon ar trebui să excludă strategia mixtă. Așadar, să luăm în considerare un alt joc legat de bătălia sexelor, în care un eșec de coordonare are mai mult sens. Acesta este jocul „puiului”. În acest joc, doi jucători se îndreaptă unul spre celălalt, încercând să îl convingă pe celălalt să cedeze și, în cele din urmă, să se abată într-un șanț. Dacă amândoi se abat în șanț, vom numi rezultatul o remiză și amândoi primesc zero. Dacă unul virează și celălalt nu virează, șoferul care virează pierde, iar celălalt șofer câștigă, iar câștigătorul primește un punct.Rețineți că adăugarea unei constante la câștigurile unui jucător sau înmulțirea câștigurilor acelui jucător cu o constantă pozitivă nu afectează echilibrele Nash – pure sau mixte. Prin urmare, putem lăsa întotdeauna un rezultat pentru fiecare jucător să fie zero și un alt rezultat să fie unu. Singura întrebare rămasă este ce se întâmplă atunci când niciunul dintre ele nu cedează, caz în care rezultă un accident. În această versiune, câștigul a fost stabilit la de patru ori mai mare decât pierderea cauzată de viraj, așa cum se arată în figura 16.18 „Puiul”, dar puteți schimba jocul și să vedeți ce se întâmplă.
Figura 16.18 Puiul
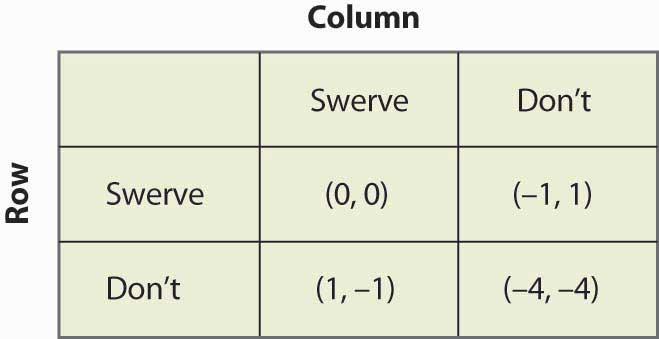
Acest joc are două echilibre de strategie pură: (Swerve, Don’t) și (Don’t, Swerve). În plus, are o strategie mixtă. Să presupunem că Column swerves cu probabilitatea p. Atunci Row obține 0p + -1(1 – p) de la swerving, 1p + (-4)(1 – p) de la not swerving, iar Row va randomiza dacă acestea sunt egale, ceea ce necesită p = ¾. Altfel spus, probabilitatea ca Columna să se abată într-un echilibru de strategie mixtă este ¾. Puteți verifica dacă jucătorul din rând are aceeași probabilitate, stabilind probabilitatea ca Rândul să se abțină egală cu q și calculând câștigurile așteptate ale Coloanei. Astfel, probabilitatea unei coliziuni este de 1/16 în echilibrul de strategie mixtă.
Equilibrul de strategie mixtă este mai probabil, într-un anumit sens, în acest joc: Dacă jucătorii ar ști deja cine va ceda, ei nu ar mai avea nevoie de fapt să joace jocul. Întregul scop al jocului este de a afla cine va ceda, ceea ce înseamnă că nu se știe dinainte. Acest lucru înseamnă că echilibrul de strategie mixtă este, într-un anumit sens, echilibrul cel mai rezonabil.
Figura 16.19 Piatră, hârtie, foarfecă
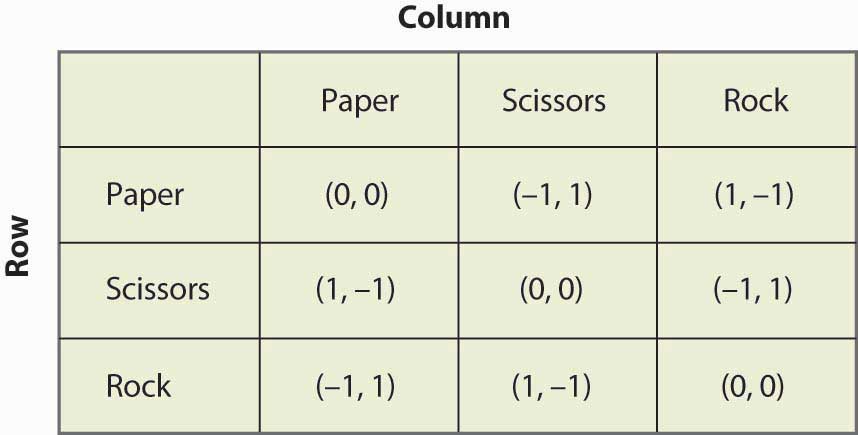
„Piatră, hârtie, foarfecă” este un joc de copii în care doi copii își folosesc mâinile pentru a alege simultan hârtie (mâna ținută plată), foarfecă (mâna cu două degete ieșite în afară pentru a arăta ca o foarfecă) sau piatră (mâna în pumn). Natura câștigurilor este că hârtia bate piatra, piatra bate foarfeca, iar foarfeca bate hârtia. Acest joc are structura care este ilustrată în figura 16.19 „Piatră, hârtie, foarfecă”.
Key Takeaways
- Un echilibru Nash cu strategie mixtă implică cel puțin un jucător care joacă o strategie aleatorie și nici un jucător nu este capabil să își mărească câștigul așteptat jucând o strategie alternativă.
- Un echilibru Nash fără aleatorizare se numește echilibru Nash cu strategie pură.
- Dacă un jucător trebuie să aleagă aleatoriu două strategii, atunci ambele trebuie să producă același câștig așteptat.
- Jocul de potrivire a bănuților are o strategie mixtă și nicio strategie pură.
- Jocul bătăliei sexelor are o strategie mixtă și două strategii pure.
- Jocul găinii este similar cu bătălia sexelor și, ca și acesta, are două strategii pure și o strategie mixtă.
Exerciții
- Să fie q probabilitatea ca Row să joace Cap. Arătați că Coloană este dispus să aleagă la întâmplare, dacă și numai dacă q = ½. (Indicație: Calculați mai întâi câștigul așteptat al lui Column atunci când Column joacă Cap și apoi calculați câștigul așteptat al lui Column atunci când Column joacă Pajură. Acestea trebuie să fie egale pentru ca Column să randomizeze.)
- Demonstrați că în jocul piatră, hârtie, foarfecă nu există echilibre de strategie pură. Arătați că a juca toate cele trei acțiuni cu probabilitate egală este un echilibru de strategie mixtă.
-
Căutați toate echilibrele următoarelor jocuri:
Figura 16.20
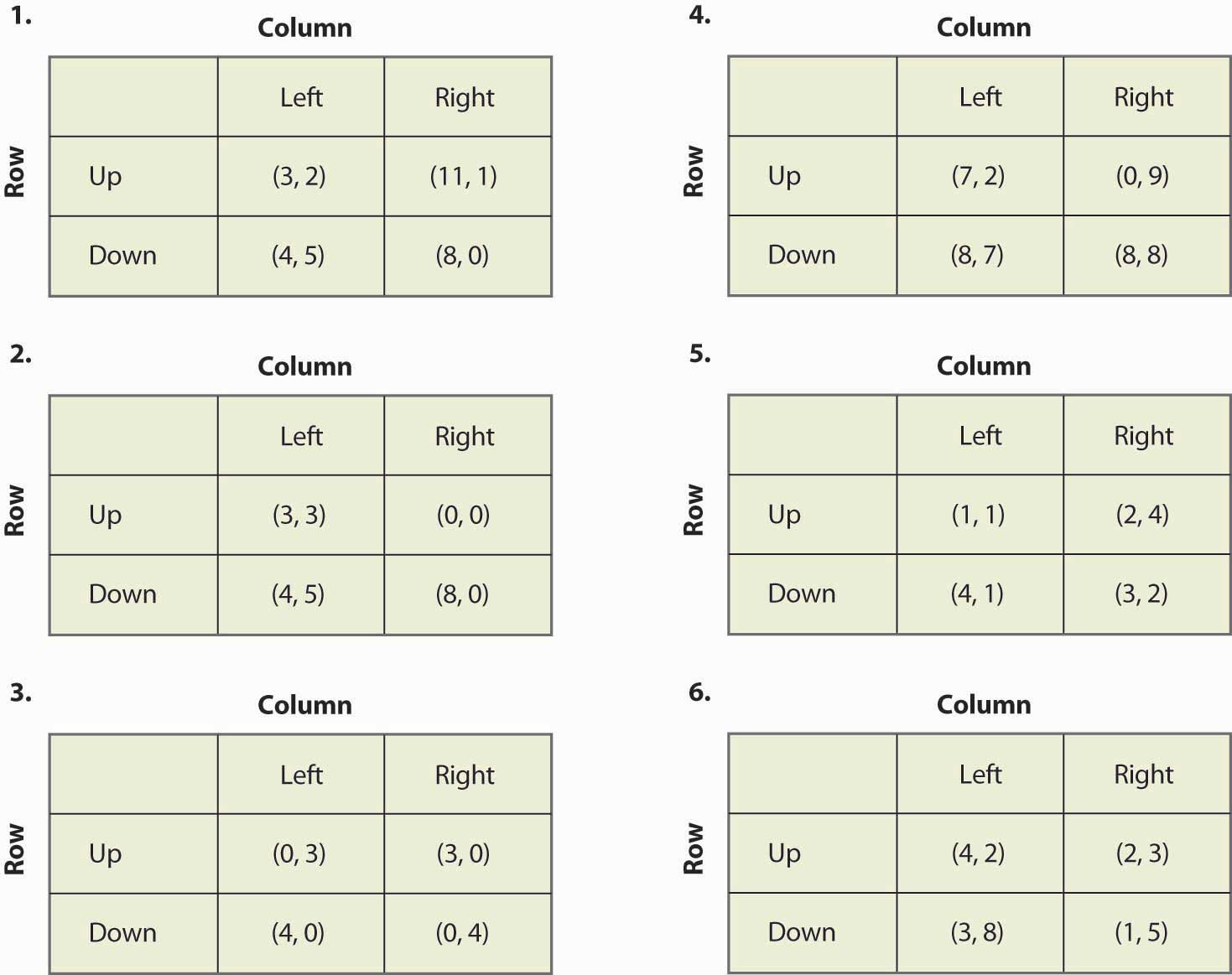
- Dacă înmulțițiți câștigul unui jucător cu o constantă pozitivă, echilibrele jocului nu se schimbă. Este adevărat sau fals acest lucru și de ce?
.