Talking in Three Dimensions

Uită-te la această imagine a unei prisme dreptunghiulare:

Câte vârfuri are? 8

Câte muchii are? 12

Câte fețe? 6

Facil, nu-i așa?

Să mai încercăm una. Aruncați o privire la această imagine a unui con:

Câte vârfuri are? Contează punctul din vârf?

Câte muchii? Hmm, nu sunt sigur. Nu ar trebui ca marginile să fie drepte?

Câte fețe? Asta e ușor! Una. Este o față circulară în partea de jos. Dar asta nu este un poligon, deci este tot o față? Oh, și cum numesc cealaltă suprafață de pe con? Fețele nu trebuie să fie plane?

O întrebare frecventă pe care o primim de la profesorii din clasele I, a II-a și a III-a se referă la modul de descriere a atributelor anumitor solide tridimensionale, în special a cilindrilor și a conurilor. Conform TEKS, elevii ar trebui să descrie solidele tridimensionale folosind limbajul geometric formal, cum ar fi vertex, edge și face. Problema este că încercăm să folosim un limbaj care funcționează pentru o clasă de forme pentru a descrie atributele unei clase complet diferite.

Formele tridimensionale precum prismele și piramidele sunt poliedre. „În geometrie, un poliedru este pur și simplu un solid tridimensional care constă dintr-o colecție de poligoane, de obicei unite la marginile lor.” (Sursa) Aceste solide au „fețe poligonale plate, muchii drepte și au colțuri sau vârfuri comune”. (Sursa)

Sferele, cilindrii și conurile, pe de altă parte, nu sunt poliedre. Ca urmare, nu putem folosi exact același limbaj pentru a le descrie sau, dacă folosim același limbaj, este cu înțelegerea faptului că definițiile nu sunt identice. Să luăm, de exemplu, cuvântul vertex.

Pe o prismă dreptunghiulară, un vertex este punctul ascuțit sau colțul în care se întâlnesc marginile. O prismă dreptunghiulară are 8 vârfuri.

Cu toate acestea, același termen poate fi folosit și pentru a descrie vârful unui con. Același termen, dar nu și aceeași definiție. După cum spune Dr. Math,

Partea cu adevărat complicată aici este că „vârful” unui con nu are nimic de-a face cu marginile, așa că are nevoie de o definiție cu totul nouă; și nu mă pot gândi la o definiție foarte bună la nivel elementar pentru ceea ce înseamnă în mod evident, care este pur și simplu un „punct.”

Pe măsură ce elevii urmăresc o matematică mai avansată, ei pot dezvolta un limbaj și definiții mai sofisticate. Între timp, cât timp sunt în școala elementară, în RRISD folosim termenul vertex of a cone pentru a descrie acest atribut al unui con.

Dacă vrem ca elevii să descrie și să clasifice acest tip de solid tridimensional, atunci trebuie să le oferim un limbaj accesibil în acest scop.

Cum rămâne cu celelalte atribute ale unui con? Din nou, scopul nostru este de a oferi un limbaj accesibil pentru elevii din clasele primare și descriptiv al acestor atribute, recunoscând că elevii noștri vor dezvolta înțelegeri mai formale mai târziu în cariera lor școlară. Pentru a descrie un con, am spune că acesta are o bază circulară, suprafața plană pe care se sprijină conul. Spunem, de asemenea, că are o muchie curbă de-a lungul bazei și o suprafață curbă care se extinde de la această muchie până la vârf.

Cum rămâne cu un cilindru? Acum că avem un limbaj accesibil pentru a descrie atributele unui con, putem extinde acest limbaj pentru a descrie atributele cilindrilor.

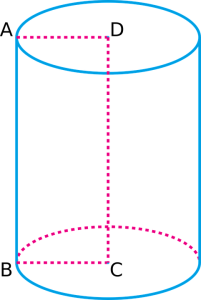
Cilindrul de mai sus este compus din două baze circulare, una în partea de sus și una în partea de jos. El are, de asemenea, două muchii curbe, una în partea superioară și una în partea inferioară. În cele din urmă, are o suprafață curbă care se întinde de la marginea de jos până la marginea de sus.

Ar trebui să adaug că atât conul cât și cilindrul pe care le-am descris sunt un con circular drept și un cilindru drept. Ca și în cazul poligoanelor și poliedrelor, există multe alte tipuri de exemple ale acestor forme. De exemplu, conul sau cilindrul ar putea fi înclinate, făcându-le oblice.

Este important ca elevii să vadă o varietate de exemple de figuri bidimensionale și tridimensionale. Cu cât întâlnesc mai multe, cu atât mai mult trebuie să se confrunte cu definițiile și terminologia lor, ceea ce servește la consolidarea înțelegerii atributelor și a modului în care acestea ne ajută să identificăm și să clasificăm aceste figuri.

Cum arată acest lucru în STAAR?

La testul lansat în 2016, STAAR a pus o întrebare care a abordat exact acest subiect și a întărit vocabularul pe care îl folosim în RRISD.

Răspunsul corect este F Nu au vârfuri. Dacă vă uitați la setul B, veți observa că acesta include un con, care, așa cum am discutat mai devreme, are un vârf. Dacă Agenția pentru Educație din Texas nu ar fi folosit termenul de vertex al unui con, atunci probabil că am fi văzut conul inclus în Setul A.

Iată un gând de despărțire de la Dr. Math:

Ce definiție folosiți depinde de ceea ce aveți de gând să faceți cu ea. Dacă doar descrieți obiecte, definiția mea liberă este bună. Dacă aveți de gând să demonstrați teoreme care implică planuri și unghiuri, veți dori să vă limitați la definiția poligonală, dar atunci nu veți pune nicio întrebare despre conuri. Cred că oamenii nu reușesc adesea să realizeze că, chiar dacă în matematică suntem speciali în ceea ce privește definițiile, aceste definiții variază de la un domeniu la altul, deoarece sunt adaptate la un anumit context. Asta este ceea ce încerc să fac aici.