Att prata i tre dimensioner

Privatkopiering & Cookies

Denna webbplats använder cookies. Genom att fortsätta godkänner du att de används. Läs mer, bland annat om hur du kontrollerar cookies.

Ta en titt på den här bilden av ett rektangulärt prisma:

Hur många hörn har det? 8

Hur många kanter? 12

Hur många sidor? 6

Lätt, eller hur?

Vi provar en annan. Ta en titt på den här bilden av en kon:

Hur många hörn har den? Räknas punkten högst upp?

Hur många kanter? Hmm, jag är inte säker. Är det inte meningen att kanterna ska vara raka?

Hur många ytor? Det är lätt! En. Det finns en cirkulär yta på botten. Men det är inte en polygon, så är det fortfarande en yta? Och vad kallar jag den andra ytan på konen? Måste inte ytor vara plana?

En vanlig fråga som vi får från lärare i årskurserna 1, 2 och 3 handlar om hur man ska beskriva egenskaperna hos vissa tredimensionella solider, särskilt cylindrar och koner. Enligt TEKS ska eleverna beskriva tredimensionella solider med hjälp av formellt geometriskt språk som t.ex. hörn, kant och yta. Problemet är att vi försöker använda ett språk som fungerar för en klass av former för att beskriva egenskaperna hos en helt annan klass.

Tredimensionella former som prismor och pyramider är polyedrar. ”Inom geometrin är en polyeder helt enkelt en tredimensionell solid som består av en samling polygoner, vanligen sammanfogade i sina kanter.” (Källa) Dessa solider har ”platta polygonala ytor, raka kanter och gemensamma hörn eller hörnpunkter”. (Källa)

Sfärer, cylindrar och koner är däremot inte polyeder. Därför kan vi inte använda exakt samma språk för att beskriva dem, eller om vi använder samma språk är det med förståelse för att definitionerna inte är identiska. Ta till exempel ordet vertex.

På ett rektangulärt prisma är en vertex den skarpa punkten eller hörnet där kanterna möts. Ett rektangulärt prisma har 8 hörn.

Men samma term kan också användas för att beskriva spetsen på en kon. Samma term, men inte samma definition. Som dr Math säger,

Den riktigt knepiga delen här är att ”vertex” i en kon inte har något att göra med kanter, så det behövs en helt ny definition; och jag kan inte komma på någon riktigt bra definition på grundskolenivå för det som de uppenbarligen menar, vilket helt enkelt är en ”punkt”.”

När eleverna ägnar sig åt mer avancerad matematik kan de utveckla ett mer sofistikerat språk och mer sofistikerade definitioner. Under tiden, medan de går i grundskolan, använder vi termen vertex of a cone i RRISD för att beskriva denna egenskap hos en kon.

Om vi vill att eleverna ska beskriva och klassificera den här typen av tredimensionell fast substans måste vi tillhandahålla ett lättillgängligt språk för det ändamålet.

Hur är det med de andra egenskaperna hos en kon? Återigen är vårt mål att tillhandahålla ett språk som är tillgängligt för grundskoleelever och som beskriver dessa attribut, med erkännande av att våra elever kommer att utveckla mer formella förståelser senare under sin skolgång. För att beskriva en kon skulle vi säga att den har en cirkulär bas, den platta yta som konen vilar på. Vi säger också att den har en böjd kant längs basen och en böjd yta som sträcker sig från denna kant upp till toppen.

Hur är det med en cylinder? Nu när vi har ett tillgängligt språk för att beskriva egenskaper hos en kon kan vi utvidga detta språk till att beskriva egenskaper hos cylindrar.

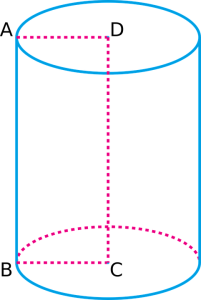
Cylindern ovan består av två cirkulära baser, en på toppen och en på botten. Den har också två böjda kanter, en längs toppen och en längs botten. Slutligen har den en krökt yta som sträcker sig från den nedre kanten upp till den övre kanten.

Jag bör tillägga att både konen och cylindern som jag har beskrivit är en högercirkulär kon och en högercylinder. Precis som med polygoner och polyedrar finns det många andra typer av exempel på dessa former. Till exempel kan konen eller cylindern vara snedställd, vilket gör dem snedställda.