Introduktion
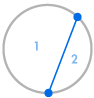
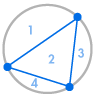
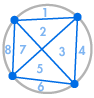
Föreställ dig att vi placerar flera punkter på cirkelns omkrets och förbinder varje punkt med varandra. Detta delar upp cirkeln i många olika områden, och vi kan räkna antalet områden i varje fall. Diagrammen nedan visar hur många regioner det finns för flera olika antal punkter på omkretsen. Vi måste se till att endast två linjer möts vid varje skärningspunkt inne i cirkeln, inte tre eller fler.
 |
 |
 |
 |
 |
| 1 region | 2 regioner | 4 regioner | 8 regioner | 16 regioner |
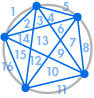
Vi kan omedelbart se ett mönster: Detta innebär att med 6 punkter på omkretsen skulle det finnas 32 regioner, och med 7 punkter skulle det finnas 64 regioner.
Vi kan besluta att vi är nöjda med detta resultat. Antalet regioner är alltid dubbelt så stort som det föregående – detta fungerade trots allt för de fem första fallen. Eller så kanske vi bestämmer oss för att kontrollera några fler, för säkerhets skull:
 |
 |
|
| 31 regioner, inte 32 | 57 regioner, inte 64 |
Tyvärr blev det något som gick fel: 31 kan se ut som ett räknefel, men 57 är mycket mindre än 64. Sekvensen fortsätter 99, 163, 256, …, mycket annorlunda än vad vi skulle få när vi fördubblar det föregående talet.
Detta exempel illustrerar varför man inom matematiken inte bara kan säga att en observation alltid är sann bara för att den fungerar i ett fåtal fall som man har testat. Istället måste man komma med ett rigoröst logiskt argument som leder från resultat som man redan känner till till något nytt som man vill visa att det är sant. Ett sådant argument kallas för ett bevis.
Beteckningar är det som gör att matematiken skiljer sig från alla andra vetenskaper, för när vi väl har bevisat något är vi helt säkra på att det är och alltid kommer att vara sant. Det är inte bara en teori som passar våra observationer och som kan ersättas av en bättre teori i framtiden.
I exemplet ovan skulle vi kunna räkna antalet skärningspunkter i cirkelns insida. Om vi tänker noggrant på förhållandet mellan antalet skärningspunkter, linjer och regioner kommer vi så småningom att få fram en annan ekvation för antalet regioner när det finns x = V.Axi punkter på cirkeln:
Antal regioner = x4 – 6 x3 + 23 x2 – 18 x + 2424 = (Math.pow(V.Axi,4) – 6*Math.pow(V.Axi,3) + 23*Math.pow(V.Axi,2) – 18*V.Axi + 24)/24.
Denna ekvation fungerar i alla fall ovan. Vi kan nu försöka bevisa den för varje värde på x med hjälp av ”induktion”, en teknik som förklaras nedan.
Traditionsenligt anges slutet på ett bevis med hjälp av ett ■ eller □, eller genom att skriva QED eller ”quod erat demonstrandum”, vilket är latin för ”det som måste visas”.
Ett resultat eller en iakttagelse som vi tror är sann kallas för en hypotes eller en gissning. När vi har bevisat det kallar vi det för en sats. När vi har bevisat en sats kan vi använda den för att bevisa andra, mer komplicerade resultat – och på så sätt bygga upp ett växande nätverk av matematiska satser.
Axiom

Raphaels skola i Aten: De antika grekiska matematikerna var de första att närma sig matematiken med hjälp av ett logiskt och axiomatiskt ramverk.
En intressant fråga är var man ska börja. Hur bevisar man den första satsen om man inte vet något ännu? Tyvärr kan man inte bevisa något med hjälp av ingenting. Du behöver åtminstone några byggstenar att börja med, och dessa kallas axiom.
Matematiker antar att axiom är sanna utan att kunna bevisa dem. Detta är dock inte så problematiskt som det kan verka, eftersom axiom antingen är definitioner eller klart uppenbara, och det finns bara väldigt få axiom. Ett axiom kan till exempel vara att a + b = b + a för alla två tal a och b.
Axiom är viktiga att få rätt, eftersom hela matematiken vilar på dem. Om det finns för få axiom kan man bevisa väldigt lite och matematiken skulle inte vara särskilt intressant. Om det finns för många axiom kan man bevisa nästan vad som helst och matematiken skulle inte heller vara intressant. Man kan inte heller ha axiom som motsäger varandra.
Matematik handlar inte om att välja rätt uppsättning axiom, utan om att utveckla ett ramverk från dessa utgångspunkter. Om man börjar med olika axiom kommer man att få en annan sorts matematik, men de logiska argumenten kommer att vara desamma. Varje område inom matematiken har sin egen uppsättning grundläggande axiom.
När matematiker har bevisat en sats publicerar de den så att andra matematiker kan kontrollera den. Ibland upptäcker de ett fel i det logiska argumentet, och ibland upptäcks ett fel inte förrän många år senare. I princip är det dock alltid möjligt att bryta ner ett bevis till de grundläggande axiomen.
Mängdteori och valets axiom

För att formulera bevis är det ibland nödvändigt att gå tillbaka till själva grunden för det språk som matematiken skrivs på: mängdteori.
En mängd är en samling objekt, till exempel tal. Elementen i en mängd skrivs vanligen inom parenteser. Vi kan hitta föreningen av två mängder (mängden element som ingår i endera mängden) eller vi kan hitta skärningspunkten mellan två mängder (mängden element som ingår i båda mängderna).
Många matematiska problem kan formuleras på mängdteorins språk, och för att bevisa dem behöver vi mängdteoretiska axiom. Med tiden har matematiker använt sig av olika samlingar av axiom, varav den mest accepterade är de nio Zermelo-Fraenkel-axiomen (ZF-axiomen):
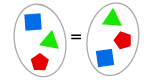
Axiom om utvidgning
Om två mängder har samma element så är de lika.
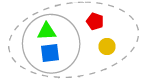
AXIOM FÖR SEPARATION
Vi kan bilda en delmängd av en mängd, som består av vissa element.

EMPTY SET AXIOM
Det finns en mängd utan medlemmar, skriven som {} eller ∅.
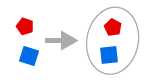
PAIR-SET AXIOM
Givet två objekt x och y kan vi bilda en mängd {x, y}.
UNION AXIOM
Vi kan bilda föreningen av två eller flera mängder.
MÄKTIGHETSMÄNGDENS AXIOM
Genom vilken mängd som helst kan vi bilda mängden av alla delmängder (maktmängden).
ODLIGHETENSAXIOM
Det finns en mängd med oändligt många element.

AXIOM AV FUNDERING
Mängder byggs upp av enklare mängder, vilket innebär att varje (icke-tom) mängd har en minimal medlem.
AXIOM FÖR ERSÄTTNING
Om vi tillämpar en funktion på varje element i en mängd är svaret fortfarande en mängd.
Om du funderar på mängdteori kommer de flesta av de här axiomen att verka helt självklara – och det är vad axiom ska vara. Det finns dock ett tionde axiom som är något mer problematiskt:
AXIOM AV VAL
Givet oändligt många icke-tomma mängder kan man välja ett element från var och en av dessa mängder.
Om man ser på det första taget ser axiomet om valfrihet (AC) precis lika oskyldigt ut som de andra ovan. Användningen av oändlighet har dock ett antal oväntade konsekvenser. Man kan till exempel använda AC för att bevisa att det är möjligt att skära en sfär i fem bitar och sätta ihop dem igen för att skapa två sfärer som var och en är identiska med den ursprungliga sfären. Detta är endast ett teoretiskt koncept – de nödvändiga styckningarna är fraktala, vilket innebär att de inte kan existera i verkligheten, och vissa av bitarna är ”icke-mätbara”, vilket innebär att de inte har någon definierad volym. Men det faktum att valets axiom kan användas för att konstruera dessa omöjliga snitt är ganska oroande.
Det finns en passionerad debatt bland logiker, huruvida man ska acceptera valets axiom eller inte. Varje samling axiom bildar en liten ”matematisk värld”, och olika satser kan vara sanna i olika världar. Det är egentligen bara en fråga om man är nöjd med att leva i en värld där man kan göra två sfärer av en…
Proof by Induction
Proof by Induction är en teknik som kan användas för att bevisa att ett visst påstående är sant för alla naturliga tal 1, 2, 3, … ”Uttalandet” är vanligen en ekvation eller en formel som innehåller en variabel n, som kan vara vilket naturligt tal som helst. Låt oss beteckna påståendet som tillämpas på n med S(n). Här är de fyra stegen i matematisk induktion:
- Först bevisar vi att S(1) är sant, dvs. att påståendet S är sant för 1.
- Nu antar vi att S(k) är sant, dvs. att påståendet S är sant för ett visst naturligt tal k.
- Med hjälp av detta antagande försöker vi härleda att S(k + 1) också är sant. När S är sant för ett tal är det alltså också sant för nästa tal.
- Då vi vet att S(1) är sant, måste S(2) vara sant. Och därför måste S(3) vara sant. Och därför måste S(4) vara sant. Och så vidare:

Induktionen kan jämföras med fallande dominobrickor: när en dominobricka faller, faller också nästa. Det första steget, att bevisa att S(1) är sant, startar den oändliga kedjereaktionen.
Det första steget förbises ofta, eftersom det är så enkelt. I själva verket är det mycket viktigt och hela induktionskedjan beror på det – vilket några av följande exempel kommer att visa…
Spelet Towers of Hanoi går ut på att flytta ett antal skivor från en pinne till en annan. Du får bara flytta en skiva åt gången och du får inte lägga en större skiva ovanpå en mindre. Försök att flytta tornet av skivor från den första pinnen till den sista pinnen, med så få drag som möjligt:
Antal skivor: Start Over Moves: Antal diskar: Antal diskar: Antal diskar: Antal diskar: Antal start över 0
När vi har förstått spelreglerna kan vi försöka hitta det minsta antalet steg som behövs, givet ett valfritt antal skivor. Att leka med spelet ovan kan leda oss till att konstatera att man med n skivor behöver minst 2n – 1 steg. Låt oss kalla detta påstående för S(n).
S(1) är uppenbarligen sant eftersom man med bara en skiva bara behöver ett drag, och 21 – 1 = 1.
Låt oss nu anta att S(k) är sant, dvs. att man behöver 2k – 1 steg för k skivor. Om vi då har k + 1 skivor:
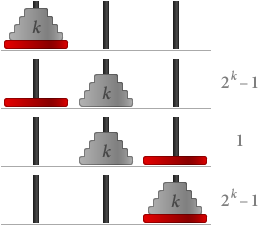
Totalt behöver vi (2k – 1) + 1 + (2k – 1) = 2(k+1) – 1 steg. Detta innebär att S(k + 1) också är sant.
Med matematisk induktion är S(n) sant för alla värden på n, vilket innebär att det effektivaste sättet att flytta n = V.Hanoi-skivor kräver 2n – 1 = Math.pow(2,V.Hanoi)-1 steg. ■
Låt oss använda induktion för att bevisa att summan av de första n naturliga talen är n (n + 1)2. Vi kontrollerar först ekvationen för små värden av n:
1 = 1 (1 + 1)2.
1 + 2 = 2 (2 + 1)2 = 3.
Nästan antar vi att resultatet är sant för k, dvs. att 1 + 2 + … + k = k (k + 1)2, där k är något tal som vi inte anger. Nu
1 + 2 + … + k + (k + 1) = k (k + 1)2 + (k + 1) = (k + 1) (k + 2)2 = (k + 1) 2.
Vi har just bevisat att om ekvationen är sann för ett visst k, så är den också sann för k + 1. Genom matematisk induktion är ekvationen sann för alla värden på n. ■
Det finns ett annat smart sätt att bevisa ekvationen ovan, som inte använder sig av induktion. Enligt uppgift upptäckte Carl Friedrich Gauss (1777 – 1855), en av historiens största matematiker, denna metod i grundskolan, när hans lärare bad honom addera alla heltal från 1 till 100.
Med hjälp av induktion vill vi bevisa att alla människor har samma hårfärg. Låt S(n) vara påståendet att ”varje grupp med n människor har samma hårfärg”.
Det är uppenbart att S(1) är sant: i varje grupp med bara en person har alla samma hårfärg.
Antag nu S(k), att i varje grupp med k personer har alla samma hårfärg. Om vi ersätter någon i gruppen med någon annan, är de fortfarande sammanlagt k och har därmed samma hårfärg. Detta fungerar för alla ursprungliga grupper av människor, vilket innebär att alla grupper av k + 1 också har samma hårfärg. Därför är S(k + 1) sant.
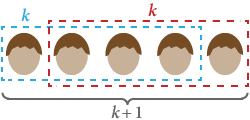
Med matematisk induktion har alla människor samma hårfärg! ■
Det är uppenbart att något måste ha gått fel i beviset ovan – alla har trots allt inte samma hårfärg. Kan du hitta felet?
Vissa satser kan inte riktigt bevisas med hjälp av induktion – vi måste använda en något modifierad version som kallas stark induktion. I stället för att anta S(k) för att bevisa S(k + 1) antar vi alla S(1), S(2), … S(k) för att bevisa S(k + 1). Allt som kan bevisas med hjälp av (svag) induktion kan uppenbarligen också bevisas med hjälp av stark induktion, men inte tvärtom.
Aritmetikens fundamentala sats säger att varje heltal som är större än 1 antingen är ett primtal, eller så kan det skrivas som en produkt av primtal på ett i princip unikt sätt.
Vi kan bevisa delar av den med hjälp av stark induktion: låt S(n) vara påståendet att ”heltalet n är ett primtal eller kan skrivas som en produkt av primtal”. S(1) är ett undantag, men S(2) är helt klart sant eftersom 2 är ett primtal.
Låt oss nu anta att S(1), S(2), …, S(k) alla är sanna, för något heltal k. Vi vet att k + 1 antingen är ett primtal eller har faktorer mindre än k + 1. Genom vårt antagande vet vi att dessa faktorer kan skrivas som en produkt av primtal. Om det inte är primtal kan därför k + 1 också skrivas som en produkt av primtal. Detta innebär att S(k + 1) är sant.
Med stark induktion är S(n) sant för alla tal n större än 1. ■
För att bevisa att denna primfaktorisering är unik (om man inte räknar med olika ordningar av faktorerna) krävs mer arbete, men det är inte särskilt svårt.
Det visar sig att principen om svag induktion och principen om stark induktion är ekvivalenta: var och en implicerar den andra. De är också båda ekvivalenta till en tredje sats, välordningsprincipen: varje (icke-tom mängd) av naturliga tal har ett minimalt element, som är mindre än alla andra.
Välordningsprincipen är den definierande egenskapen hos de naturliga talen. Det är ett av de grundläggande axiom som används för att definiera de naturliga talen ![]() = {1, 2, 3, …}. Dessa axiom kallas Peanoaxiom, uppkallade efter den italienske matematikern Guiseppe Peano (1858 – 1932).
= {1, 2, 3, …}. Dessa axiom kallas Peanoaxiom, uppkallade efter den italienske matematikern Guiseppe Peano (1858 – 1932).
Bevis genom motsägelse
Bevis genom motsägelse är en annan viktig bevisteknik. Om vi vill bevisa ett påstående S antar vi att S inte var sant. Med hjälp av detta antagande försöker vi härleda ett falskt resultat, till exempel 0 = 1. Om alla våra steg var korrekta och resultatet är falskt måste vårt ursprungliga antagande ha varit fel. Vårt ursprungliga antagande var att S inte är sant, vilket innebär att S faktiskt är sant.
Denna teknik kan användas under många olika omständigheter, t.ex. för att bevisa att √2 är irrationellt, bevisa att de verkliga talen är oräkneliga eller bevisa att det finns oändligt många primtal.
Här är ett annat roligt exempel:
Vi kan använda bevis genom motsägelse, tillsammans med principen om god ordning, för att bevisa att alla naturliga tal är ”intressanta”.
Förutsätt att inte alla naturliga tal är intressanta, och låt S vara mängden ointressanta tal. Enligt principen om god ordning har S en minsta medlem x som är det minsta icke-intressanta talet. Denna märkliga egenskap gör uppenbarligen x till ett särskilt intressant tal. Detta är en motsägelse eftersom vi antog att x var ointressant.
Därmed är alla tal intressanta. ■
Gödel och obevisbara satser

Kurt Gödel (1906-1978)
I början av 1900-talet började matematiken växa snabbt och tusentals matematiker arbetade inom otaliga nya områden. David Hilbert (1862 – 1943) satte upp ett omfattande program för att formalisera matematiken och lösa eventuella inkonsekvenser i matematikens grunder. I detta ingick att bevisa alla satser med hjälp av en uppsättning enkla och universella axiom, att bevisa att denna uppsättning axiom är konsekvent och att bevisa att denna uppsättning axiom är fullständig, dvs. att varje matematiskt påstående kan bevisas eller motbevisas med hjälp av axiomen.
Olyckligtvis förstördes dessa planer av Kurt Gödel år 1931. Han bevisade att i varje (tillräckligt komplext) matematiskt system med en viss uppsättning axiom kan man hitta vissa påståenden som varken kan bevisas eller motbevisas med hjälp av dessa axiom. Det är inte heller möjligt att bevisa att en viss uppsättning axiom är konsistent med hjälp av enbart axiomen i sig.
Gödels upptäckt bygger på det faktum att en uppsättning axiom inte kan användas för att säga något om sig själv, till exempel om den är konsistent. Problem med självreferenser finns inte bara inom matematiken utan även inom språket. Här är lögnarparadoxen:
”Denna mening är falsk.”
Satsen ovan försöker säga något om sig själv. Om den är sann säger meningen att den är falsk. Om den är falsk säger meningen att den inte är falsk, dvs. att den är sann. I själva verket är meningen varken sann eller falsk.
När Gödels satser först publicerades var de djupt oroande för många matematiker. När man sätter sig för att bevisa en observation vet man inte om det finns ett bevis – resultatet kan vara sant men obestridligt. I dag vet vi att ofullständighet är en grundläggande del inte bara av logiken utan även av datavetenskapen, som bygger på maskiner som utför logiska operationer.
Förvånansvärt nog är det möjligt att bevisa att vissa påståenden är omöjliga att bevisa. Ett exempel är kontinuumshypotesen, som handlar om storleken på oändliga mängder.
Till slutet av sitt liv utvecklade Kurt Gödel allvarliga psykiska problem och han dog av självhunger 1978. Hans insikter om logikens grunder var de mest djupgående sedan de gamla grekernas utveckling av bevisföring.