
Bertrand Russell (1872-1970) och A.N. Whitehead (1861-1947)
Bertrand Russell och Alfred North Whitehead var brittiska matematiker, logiker och filosofer som stod i spetsen för den brittiska revolten mot den kontinentala idealismen i början av 1900-talet och som tillsammans gjorde viktiga bidrag inom områdena matematisk logik och mängdteori.
Whitehead var den äldste av de två och kom från en mer ren matematisk bakgrund. Han blev Russells lärare vid Trinity College i Cambridge på 1890-talet och samarbetade sedan med sin mer berömda före detta elev under 1900-talets första decennium med deras monumentala verk ”Principia Mathematica”. Efter första världskriget, som Russell tillbringade en stor del av i fängelse på grund av sin pacifistiska verksamhet, avstannade dock samarbetet, och Whiteheads akademiska karriär stod därefter i skuggan av den mer flamboyante Russells. Han emigrerade till USA på 1920-talet och tillbringade resten av sitt liv där.
Russell föddes i en välbärgad familj inom den brittiska aristokratin, även om hans föräldrar var extremt liberala och radikala för sin tid. Hans föräldrar dog när Russell var ganska ung och han uppfostrades till stor del av sin övertygat viktorianska (om än ganska progressiva) mormor. Hans ungdomsår var mycket ensamt och han led av depressioner och hävdade senare att det bara var hans kärlek till matematiken som hindrade honom från att begå självmord. Han studerade matematik och filosofi vid Cambridge University under G.E. Moore och A.N. Whitehead, där han utvecklades till en innovativ filosof, en produktiv författare i många ämnen, en övertygad ateist och en inspirerad matematiker och logiker. Idag anses han vara en av grundarna av den analytiska filosofin, men han skrev om nästan alla större områden inom filosofin, särskilt metafysik, etik, epistemologi, matematikfilosofi och språkfilosofi.
Russell var en engagerad och profilerad politisk aktivist under hela sitt långa liv. Han var en framstående antikrigsaktivist under både första och andra världskriget, förespråkade frihandel och antiimperialism och blev senare en stark kampanjarbetare för kärnvapennedrustning och socialism samt mot Adolf Hitler, sovjetisk totalitarism och USA:s inblandning i Vietnamkriget.
Russells paradox
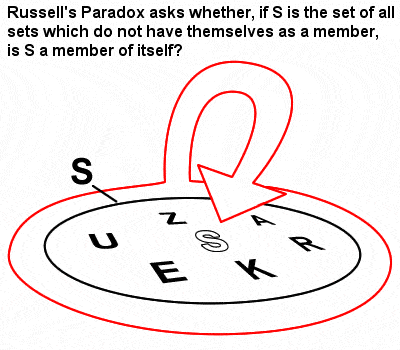
Russells paradox
Russells matematik påverkades i hög grad av den mängdteori och logik Gottlob Frege hade utvecklat i kölvattnet av Cantors banbrytande tidiga arbete om mängder. I sin ”The Principles of Mathematics” från 1903 identifierade han dock vad som kommit att kallas Russells paradox (en mängd som innehåller mängder som inte är medlemmar av sig själva), vilket visade att Freges naiva mängdteori faktiskt kunde leda till motsägelser.
Paradoxen illustreras ibland med detta förenklade exempel: ”Om en barberare rakar alla och endast de män i byn som inte rakar sig själva, rakar han då sig själv?”
Paradoxen tycktes innebära att man inte längre kunde lita på själva grunderna för hela matematiken, och att sanningen, även inom matematiken, aldrig skulle kunna vara absolut känd (Gödels och Turings senare arbeten skulle bara göra detta värre). Russells kritik var tillräcklig för att rubba Freges förtroende för hela logikens uppbyggnad, och han var nådig nog att öppet erkänna detta i ett hastigt skrivet tillägg till volym II av hans ”Basic Laws of Arithmetic”.
Men Russells magnum opus var den monolitiska ”Principia Mathematica”, som publicerades i tre volymer 1910, 1912 och 1913. Den första volymen skrevs tillsammans med Whitehead, även om de två senare volymerna nästan helt och hållet var Russells verk. Ambitionen med detta ambitiösa verk var inget mindre än ett försök att härleda hela matematiken från rent logiska axiom, samtidigt som man undvek den typ av paradoxer och motsägelser som fanns i Freges tidigare arbete om mängdteori. Russell uppnådde detta genom att använda en teori eller ett system av ”typer”, där varje matematisk enhet tilldelas en typ inom en hierarki av typer, så att objekt av en viss typ uteslutande byggs upp av objekt av föregående typer längre ner i hierarkin, vilket förhindrar slingor. Varje uppsättning av element är alltså av en annan typ än var och en av sina element, så att man inte kan tala om ”uppsättningen av alla uppsättningar” och liknande konstruktioner, som leder till paradoxer.
I ”Principia” krävdes emellertid, förutom typteorins grundläggande axiom, ytterligare tre axiom som tycktes inte vara sanna som rena logiska frågor, nämligen ”oändlighetsaxiomet” (som garanterar existensen av minst en oändlig mängd, nämligen mängden av alla naturliga tal), ”valfrihetsaxiomet” (som säkerställer att, givet en samling av ”behållare”, var och en innehåller minst ett föremål, det är möjligt att göra ett urval av exakt ett föremål från varje behållare, även om det finns oändligt många behållare, och att det inte finns någon ”regel” för vilket föremål som ska väljas från varje behållare) och Russells eget ”reducerbarhetsaxiom” (som anger att varje påståendes sanningsfunktion kan uttryckas med en formellt likvärdig predikativ sanningsfunktion).
Under det tiotal år som Russell och Whitehead ägnade åt ”Principia” påbörjades och övergavs utkast efter utkast eftersom Russell ständigt omprövade sina grundläggande premisser. Russell och hans fru Alys flyttade till och med in hos Whiteheads för att påskynda arbetet, även om hans eget äktenskap blev lidande då Russell blev förälskad i Whiteheads unga fru Evelyn. Till slut insisterade Whitehead på att verket skulle publiceras, även om det inte var (och kanske aldrig skulle bli) färdigt, även om de var tvungna att publicera det på egen bekostnad eftersom inga kommersiella förläggare ville röra det.
Principia Mathematica

En liten del av det långa beviset på att 1+1 =2 i ”Principia Mathematica”
En viss uppfattning om ”Principia ”s räckvidd och omfång kan utläsas av det faktum att det tar mer än 360 sidor att slutgiltigt bevisa att 1 + 1 = 2.
I dag anses det allmänt vara ett av de viktigaste och mest banbrytande verken inom logiken sedan Aristoteles ”Organon”. Den verkade anmärkningsvärt framgångsrik och motståndskraftig i sina ambitiösa mål, och snart blev Russell och Whitehead världsberömda. Det var faktiskt först Gödels ofullständighetssats från 1931 som slutligen visade att ”Principia” inte kunde vara både konsekvent och fullständig.
Russell tilldelades 1949 Order of Merit och året därpå Nobelpriset i litteratur. Hans berömmelse fortsatte att växa, även utanför akademiska kretsar, och han blev något av ett känt namn senare i livet, även om det till stor del berodde på hans filosofiska bidrag och hans politiska och sociala aktivism, som han fortsatte med till slutet av sitt långa liv. Han dog av influensa i sitt älskade Wales vid en ålder av 97 år.
| << Tillbaka till Hardy och Ramanujan | Förward to Hilbert >> |