16.3 Blandade strategier
Lärandemål
- Vilka spel kräver eller tillåter slumpmässighet som en del av lösningen?
Vi kan återigen betrakta spelet med matchande slantar, som illustreras i figur 16.13 ”Matching pennies again”.
Figur 16.13 Matching pennies again
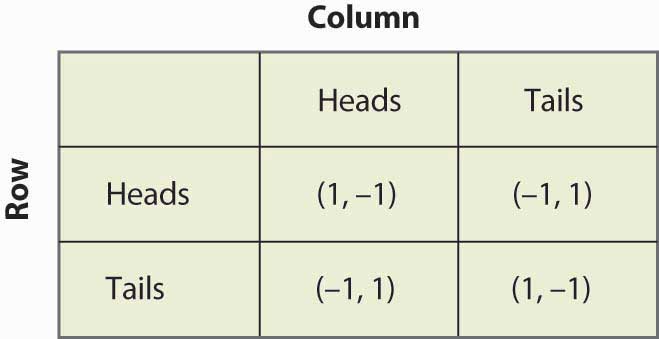
Antag att Row tror att Column spelar Heads med sannolikhet p. Om Row spelar Heads får Row 1 med sannolikhet p och -1 med sannolikhet (1 – p), vilket ger ett förväntat värde på 2p – 1. På samma sätt, om Row spelar på klave, får Row -1 med sannolikhet p (när Column spelar på krona) och 1 med sannolikhet (1 – p), för ett förväntat värde på 1 – 2p. Detta sammanfattas i figur 16.14 ”Mixed strategy in matching pennies”.
Om 2p – 1 > 1 – 2p är det i genomsnitt bättre för Row att spela Heads än Tails. På samma sätt, om 2p – 1 < 1 – 2p, är det bättre för Row att spela på klave än på krona. Om å andra sidan 2p – 1 = 1 – 2p får Row samma utdelning oavsett vad Row gör. I det här fallet kan Row spela krona, spela klave eller kasta ett mynt och randomisera Row’s spel.
En Nash-jämvikt med blandad strategiEn Nash-jämvikt där minst en spelare spelar en randomiserad strategi och ingen spelare kan öka sin förväntade avkastning genom att spela en alternativ strategi. innebär att minst en spelare spelar en randomiserad strategi och ingen spelare kan öka sin förväntade avkastning genom att spela en alternativ strategi. En Nash- jämvikt där ingen spelare randomiserar kallas en Nash- jämvikt med ren strategiEn Nash- jämvikt där ingen spelare randomiserar..
Figur 16.14 Blandad strategi vid matchning av pennies
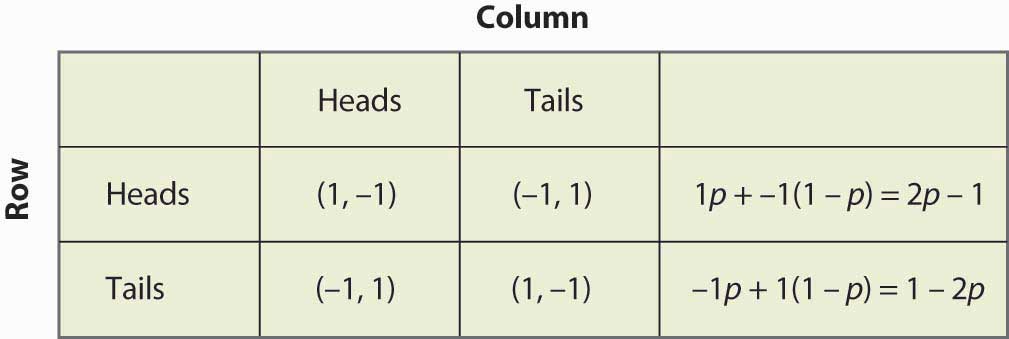
Bemärk att randomisering kräver jämlikhet i förväntade utbetalningar. Om en spelare ska randomisera över strategi A eller strategi B måste båda dessa strategier ge samma förväntade avkastning. Annars skulle spelaren föredra en av dem och inte spela den andra.
Beräkning av en blandad strategi har ett element som ofta verkar förvirrande. Anta att Row kommer att slumpmässigt välja. Då måste Row’s payoffs vara lika för alla strategier som Row spelar med positiv sannolikhet. Men denna jämlikhet i Row’s payoffs bestämmer inte sannolikheterna med vilka Row spelar de olika raderna. Istället kommer denna jämlikhet i Row’s payoffs att bestämma sannolikheterna med vilka Column spelar de olika kolumnerna. Anledningen är att det är kolonnens sannolikheter som bestämmer de förväntade vinsterna för Row; om Row kommer att slumpa måste kolonnens sannolikheter vara sådana att Row är villig att slumpa.
Så har vi till exempel beräknat vinsten för Row av att spela på krona, vilket var 2p – 1, där p var sannolikheten för att Column spelade på krona. På samma sätt var vinsten för Row att spela på Tails 1 – 2p. Row är villig att randomisera om dessa är lika, vilket löser p = ½.
Nu ska vi pröva ett något mer utmanande exempel och återuppta kampen mellan könen. Figur 16.15 ”Mixed strategy in battle of the sexes” illustrerar återigen utbetalningarna.
Figur 16.15 Mixed strategy in battle of the sexes
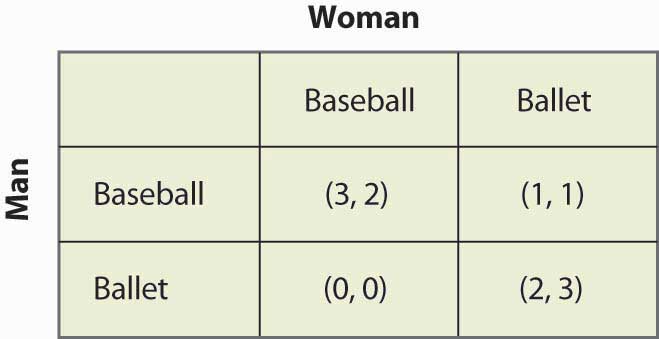
Detta spel har två Nash-jämvikter med ren strategi: (Baseball, Baseball) och (Ballet, Ballet). Finns det en blandad strategi? För att beräkna en blandad strategi, låt kvinnan gå till basebollspelet med sannolikhet p och mannen gå till basebollspelet med sannolikhet q. Figur 16.16 ”Full computation of the mixed strategy” innehåller beräkningen av utbetalningarna för den blandade strategin för varje spelare.
Figur 16.16 Fullständig beräkning av den blandade strategin
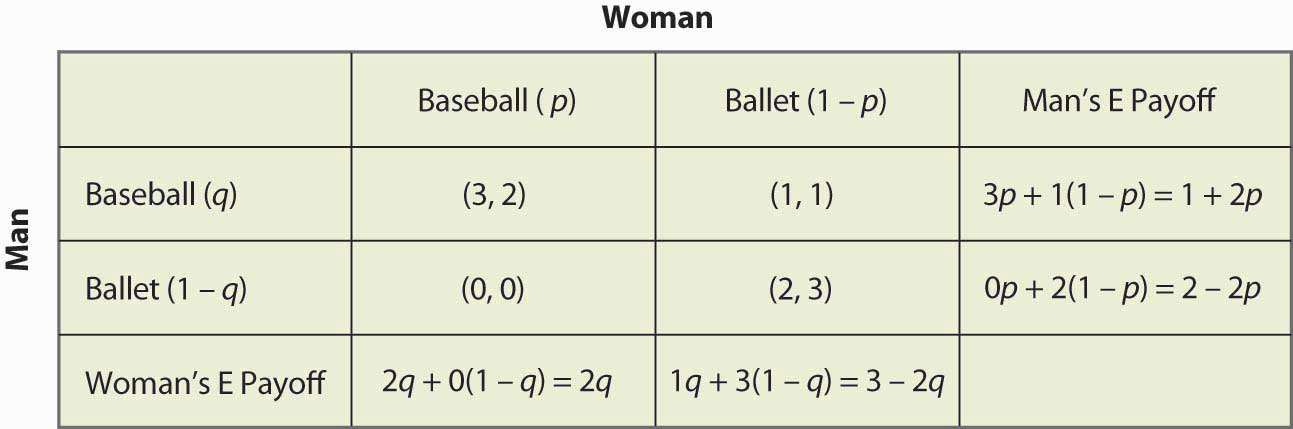
Till exempel, om mannen (radspelaren) går till basebollspelet får han 3 när kvinnan går till basebollspelet (sannolikhet p), och annars får han 1, för en förväntad utbetalning på 3p + 1(1 – p) = 1 + 2p. De andra beräkningarna är liknande, men du bör definitivt gå igenom logiken och verifiera varje beräkning.
En blandad strategi i könskampen kräver att båda parter randomiserar (eftersom en ren strategi av endera parten förhindrar randomisering av den andra). Mannens likgiltighet mellan att gå till basebollmatchen och till balen kräver 1 + 2p = 2 – 2p, vilket ger p = ¼. Det vill säga, mannen kommer att vara villig att slumpmässigt välja vilket evenemang han besöker om kvinnan går till baletten ¾ av tiden, och annars till basebollmatchen. Detta gör mannen indifferent mellan de två evenemangen eftersom han föredrar att vara med kvinnan, men han gillar också att vara på baseballmatchen. För att kompensera för den fördel som spelet innebär för honom måste kvinnan vara på baletten oftare.
För att kvinnan ska kunna slumpmässigt välja måste kvinnan på samma sätt få lika mycket utdelning av att gå på basebollmatchen och att gå på baletten, vilket kräver 2q = 3 – 2q, eller q = ¾. Sannolikheten för att mannen går till basebollmatchen är således ¾, och han går till baletten ¼ av gångerna. Dessa är oberoende sannolikheter, så för att få fram sannolikheten att båda går till basebollmatchen multiplicerar vi sannolikheterna, vilket ger 3/16. Figur 16.17 ”Sannolikheter för blandad strategi” fyller i sannolikheterna för alla fyra möjliga utfall.
Figur 16.17 Sannolikheter för blandad strategi
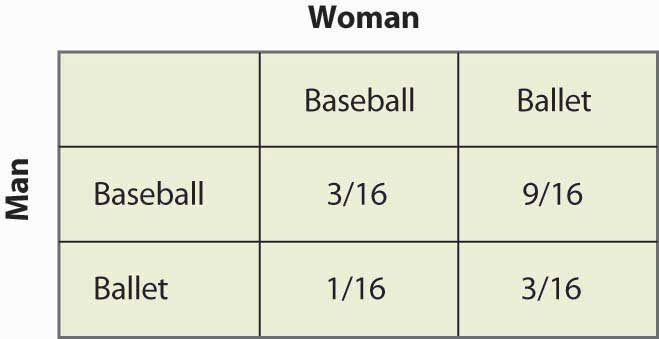
Bemärk att mer än hälften av gångerna (baseboll, balett) är utfallet av den blandade strategin och de två personerna är inte tillsammans. Denna brist på samordning är i allmänhet ett kännetecken för jämvikter med blandad strategi. De förväntade utbetalningarna för båda spelarna är också lätt att beräkna. Mannens utbetalning är 1 + 2p = 2 – 2p, och eftersom p = ¼ får mannen 1½. En liknande beräkning visar att kvinnans vinst är densamma. Båda gör alltså sämre ifrån sig än att samordna det mindre föredragna utfallet. Men denna Nash-jämvikt med blandad strategi, hur oönskad den än kan verka, är en Nash-jämvikt i den bemärkelsen att ingen av parterna kan förbättra sin egen payoff, med tanke på den andra partens beteende.
I kampen mellan könen kan en Nash-jämvikt med blandad strategi tyckas osannolik; och vi skulle kunna förvänta oss att paret samordnar sig mer effektivt. I själva verket borde ett enkelt telefonsamtal utesluta den blandade strategin. Låt oss därför överväga ett annat spel som är relaterat till kampen mellan könen, där en misslyckad samordning är mer meningsfull. Detta är spelet ”kyckling”. I detta spel kör två spelare mot varandra och försöker övertyga den andra att ge vika och till slut svänga ner i ett dike. Om båda kör in i diket kallar vi resultatet oavgjort och båda får noll poäng. Om en av dem väjer och den andra inte gör det, förlorar den förare som väjer och den andra föraren vinner, och vi ger vinnaren en poäng.Observera att om man lägger till en konstant till en spelares vinst, eller multiplicerar den spelarens vinst med en positiv konstant, så påverkar det inte Nash-jämvikterna, vare sig rena eller blandade. Därför kan vi alltid låta ett utfall för varje spelare vara noll och ett annat utfall vara ett. Den enda återstående frågan är vad som händer när ingen av dem ger utdelning, vilket i så fall leder till en krasch. I den här versionen har utdelningen satts till fyra gånger förlusten av att svänga, vilket visas i figur 16.18 ”Kyckling”, men du kan ändra spelet och se vad som händer.
Figur 16.18 Kyckling
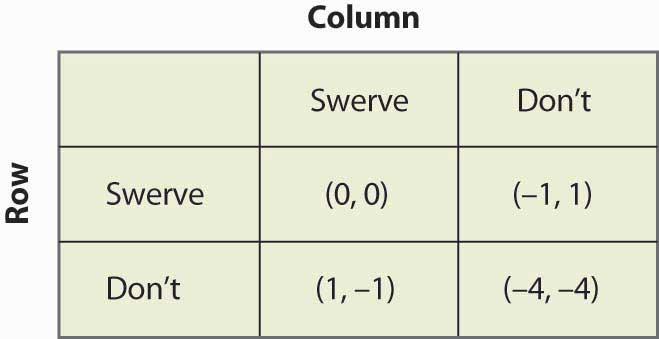
Det här spelet har två renstrategiska jämvikter: (Swerve, Don’t) och (Don’t, Swerve). Dessutom har det en blandad strategi. Anta att Column sviker med sannolikhet p. Då får Row 0p + -1(1 – p) från att svika, 1p + (-4)(1 – p) från att inte svika, och Row kommer att slumpa om dessa är lika, vilket kräver p = ¾. Det vill säga, sannolikheten för att Column swerves i en jämvikt med blandad strategi är ¾. Du kan verifiera att Row-spelaren har samma sannolikhet genom att sätta sannolikheten för att Row swerves lika med q och beräkna Column’s förväntade payoffs. Sannolikheten för en kollision är alltså 1/16 i jämvikten med blandad strategi.
Den blandade strategiska jämvikten är mer sannolik, i någon mening, i det här spelet: Om spelarna redan visste vem som skulle ge sig, skulle de faktiskt inte behöva spela spelet. Hela poängen med spelet är att ta reda på vem som kommer att ge upp, vilket innebär att det inte är känt i förväg. Detta innebär att jämvikten med blandad strategi i någon mening är den rimligare jämvikten.
Figur 16.19 Sten, papper, sax
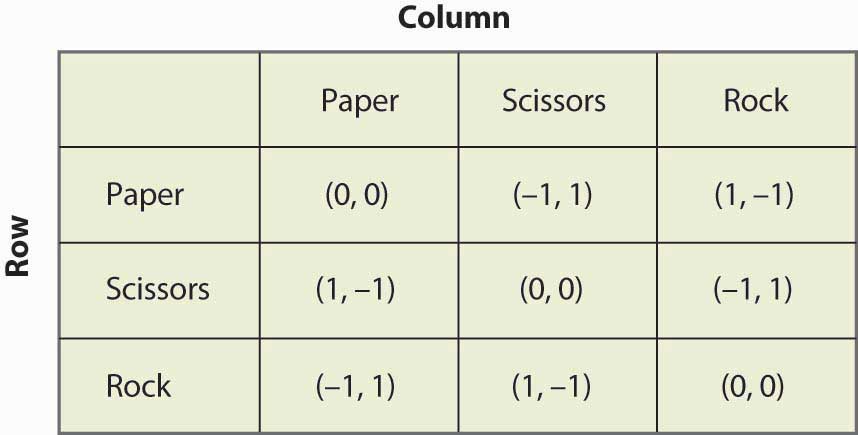
”Sten, papper, sax” är ett barnspel där två barn använder sina händer för att samtidigt välja papper (handen hålls platt), sax (handen med två fingrar som sticker ut så att det ser ut som en sax) eller sten (handen hålls i en knytnäve). Utdelningen är att papper slår sten, sten slår sax och sax slår papper. Detta spel har den struktur som illustreras i figur 16.19 ”Sten, papper, sax”.
Nyckelkunskaper
- En Nash-jämvikt med blandad strategi innebär att minst en spelare spelar en randomiserad strategi och att ingen spelare kan öka sin förväntade utdelning genom att spela en alternativ strategi.
- En Nash-jämvikt utan randomisering kallas Nash-jämvikt med ren strategi.
- Om en spelare ska slumpmässigt välja mellan två strategier måste båda ge samma förväntade avkastning.
- Spelet med matchande slantar har en blandad strategi och ingen ren strategi.
- Spelet med könsstriden har en blandad strategi och två rena strategier.
- Spelet med kyckling liknar könskampen och har liksom den två rena strategier och en blandad strategi.
Övningar
- Låt q vara sannolikheten för att Row spelar Heads. Visa att Column är villig att randomisera om och endast om q = ½. (Tips: Beräkna först Kolonnens förväntade vinst när Kolonn spelar krona, och beräkna sedan Kolonnens förväntade vinst när Kolonn spelar klave. Dessa måste vara lika för att Column ska randomisera.)
- Visa att det i spelet sten, papper, sax inte finns några jämvikter med ren strategi. Visa att det är en jämvikt med blandad strategi att spela alla tre handlingar med samma sannolikhet.
-
Finn alla jämvikter i följande spel:
Figur 16.20
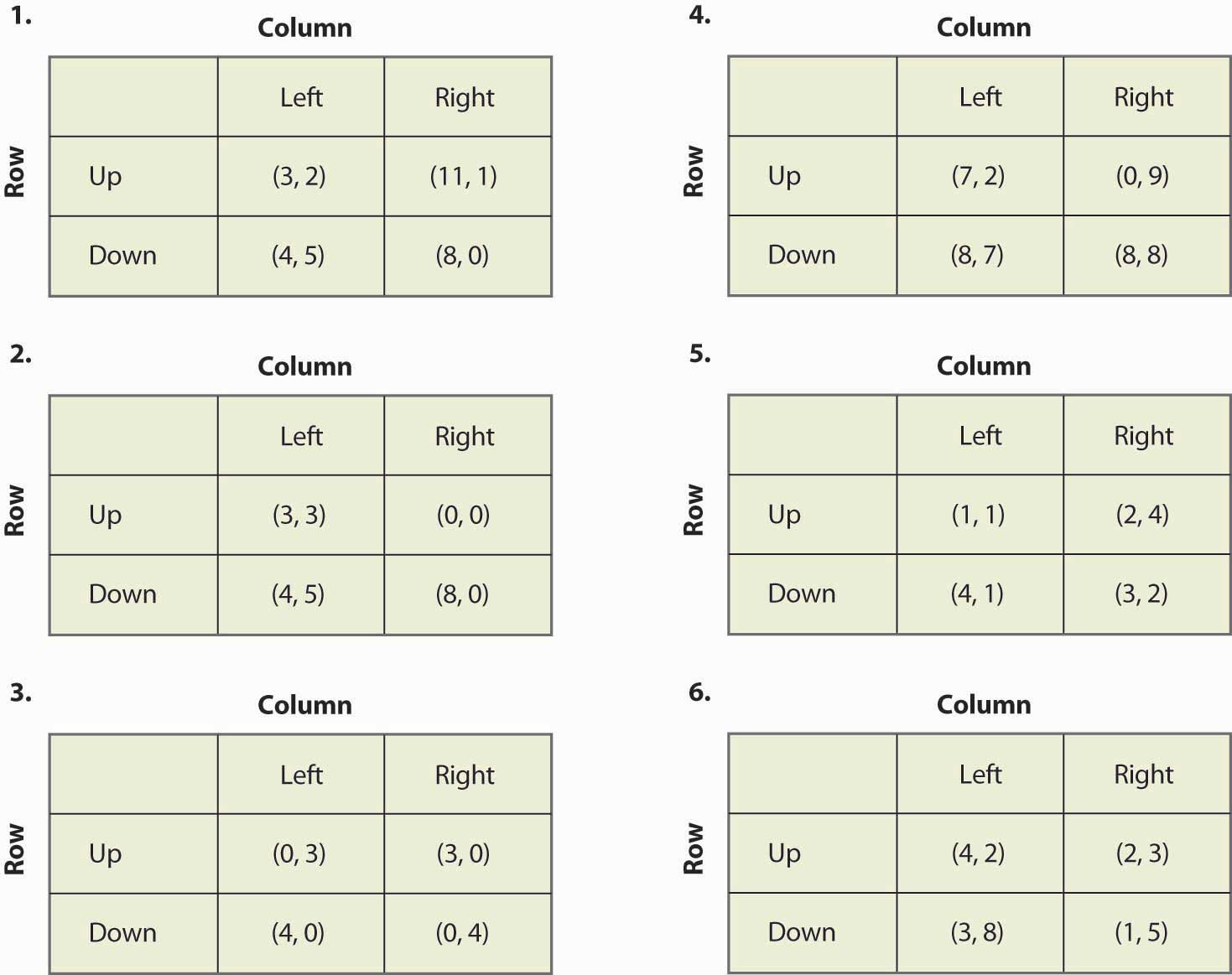
- Om du multiplicerar en spelares utbetalning med en positiv konstant förändras inte jämvikterna i spelet. Är detta sant eller falskt och varför?