Delta-Delta Ct-metoden eller Livak-metoden är den mest föredragna metoden för analys av qPCR-data. Den kan dock endast användas när vissa kriterier är uppfyllda, se föreläsningsanteckningarna för att försäkra dig om att dessa kriterier är uppfyllda. Om så inte är fallet används en mer generaliserad metod som kallas Pfaffl-metoden. Läs det kompletterande läsmaterialet för att få mer information om denna metod.
Här är stegen för Livak-metoden:
Excel-filen med alla beräkningar finns i mappen qPCR-analys på Blackboard.
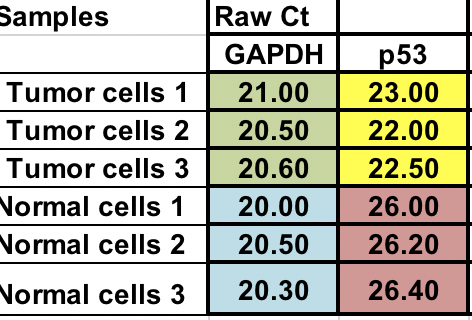
Du har rå Ct (antal cykler som krävs för att nå tröskelvärdet) för normala och tumörceller (3 replikat för vardera).
Normalisering¶
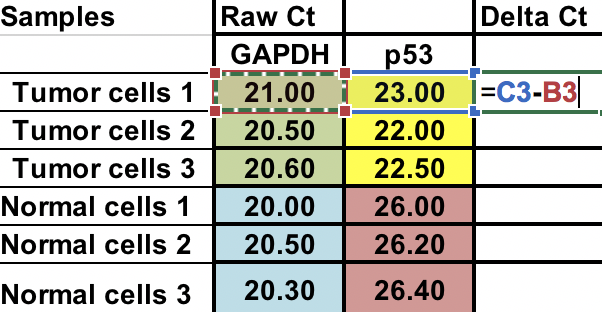
Först måste du beräkna den relativa skillnaden mellan den aktuella genen (p53) och husets gen (GAPDH).
∆Ct = Ct (gen av intresse) – Ct (hushållsgen)
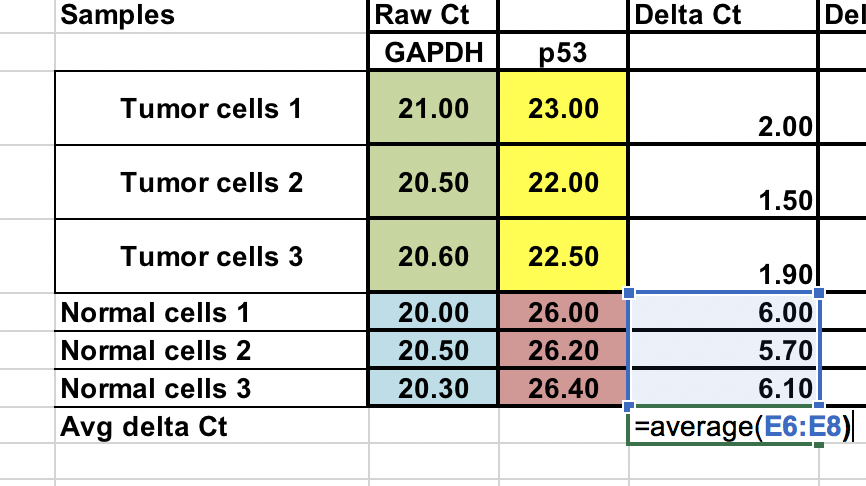
Genomsnittet av kontrollproverna (normala celler)¶
Vidare jämför vi vår tumör (behandling) med kontrollen (normala celler), måste vi först beräkna medelvärdet av ∆Ct för de tre kontrollproverna (normala celler).
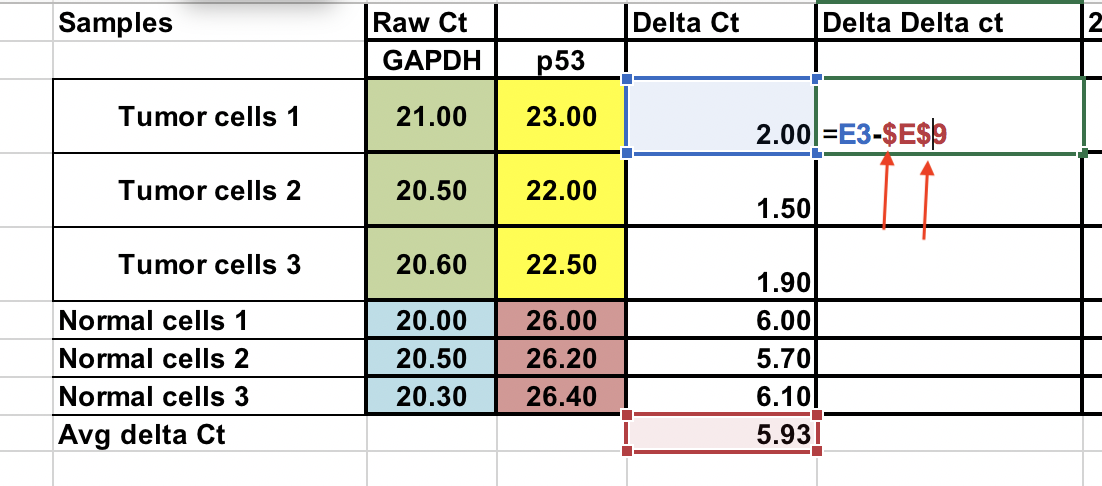
Beräkna ∆∆Ct i förhållande till genomsnittet av ∆Ct normal. celler¶
∆∆Ct = ∆Ct (tumörprov) – ∆Ct (normalt genomsnitt)
Du kan göra detta även med normala prov. Använd $-tecken framför kolumnnummer och råbokstav (pilar) för att fixera cellen.
Fold genexpression för varje prov¶
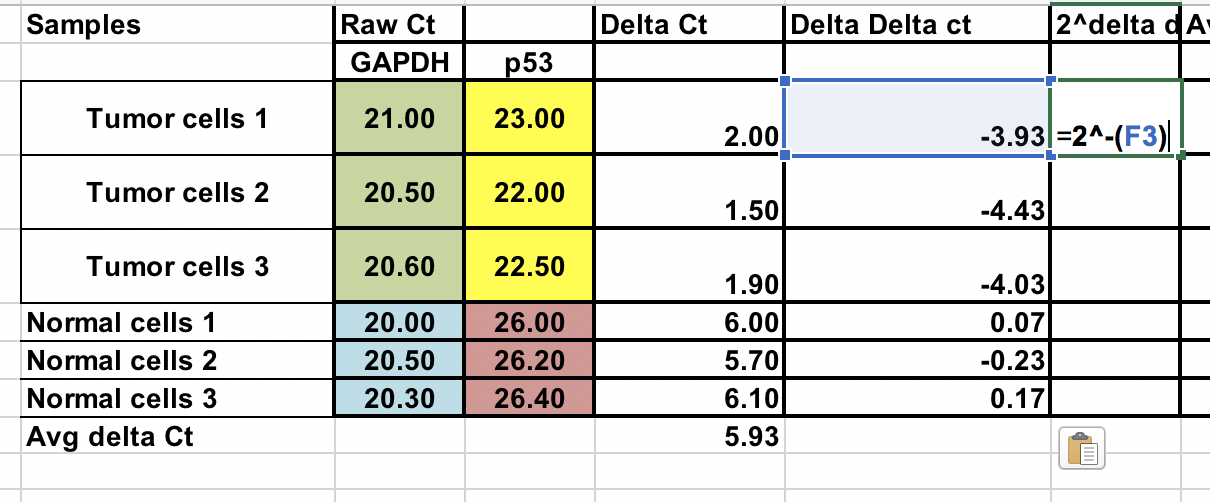
Se till att du höjer det negativa ∆∆Ct till en potens av två.
Fold gene expression = 2^-(∆∆Ct)
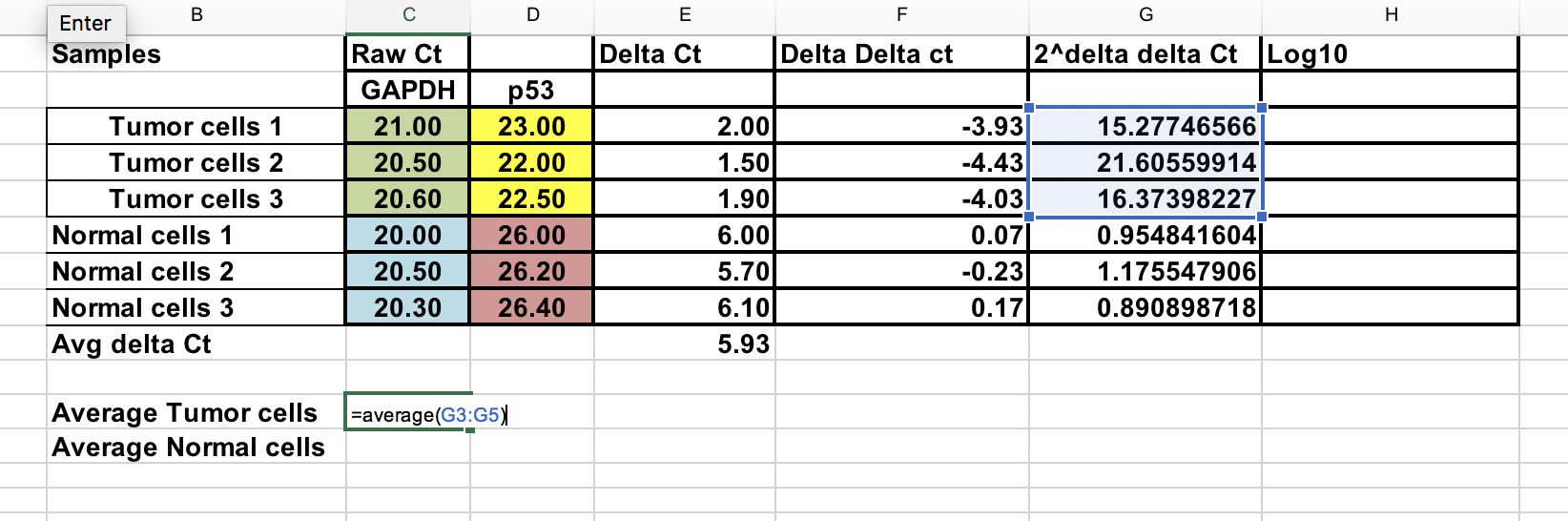
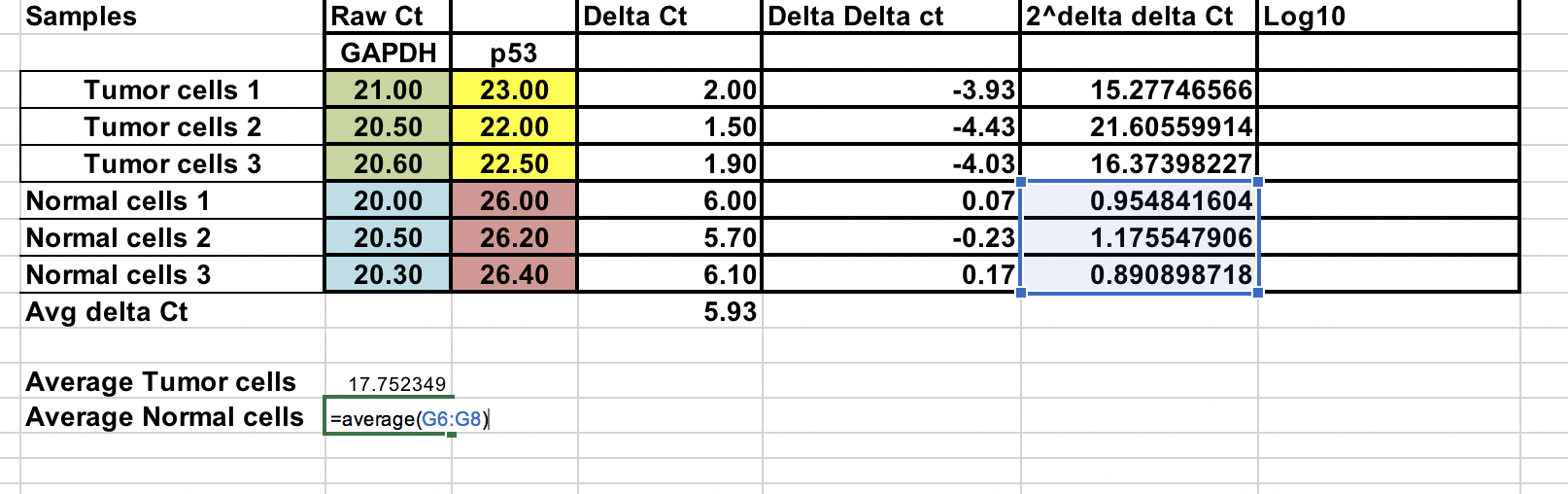
Overall fold change¶
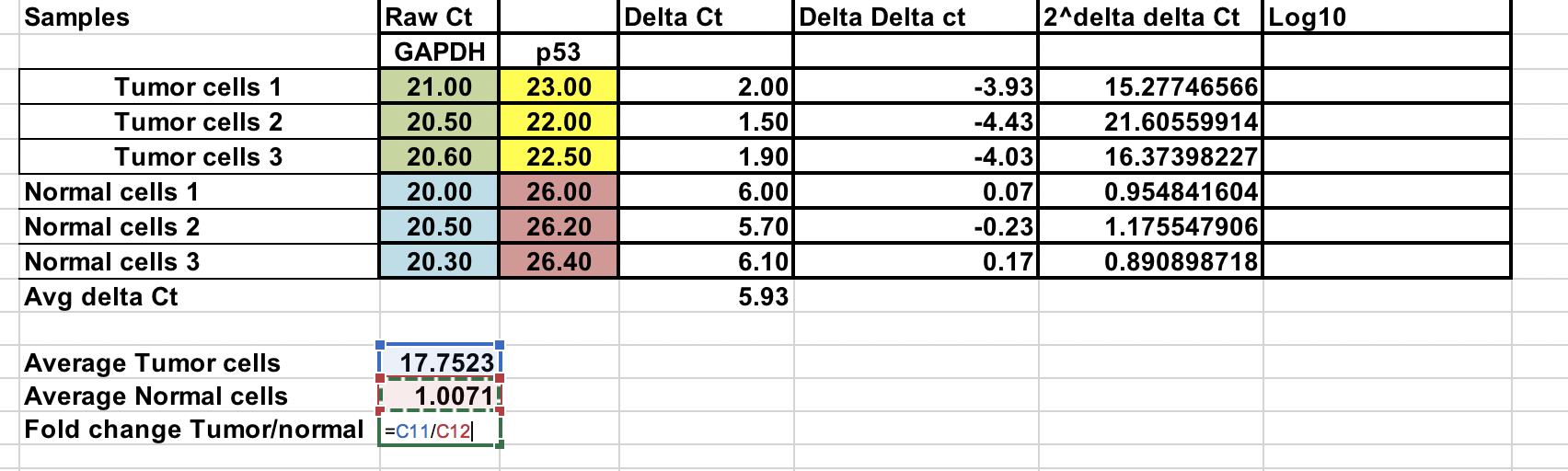
Du kan beräkna genomsnittlig fold change för både tumör- och normalprov. Förhållandet mellan dessa två är fold change mellan tumör- och normalprover.
Logtransformation¶
För att kunna utföra parametriska statistiska tester, t.ex. T-test, är det tillrådligt att omvandla de slutgiltiga genuttrycksresultaten till logaritmiska värden (valfri logbas). Detta skulle göra datafördelningen symmetrisk.
Här har vi ändrat 2^-(∆∆Ct) till log 10.
T-test¶
Det är nödvändigt att vara försiktig när man använder parametriska tester om data inte är normalfördelade, det skulle leda till felaktiga slutsatser.
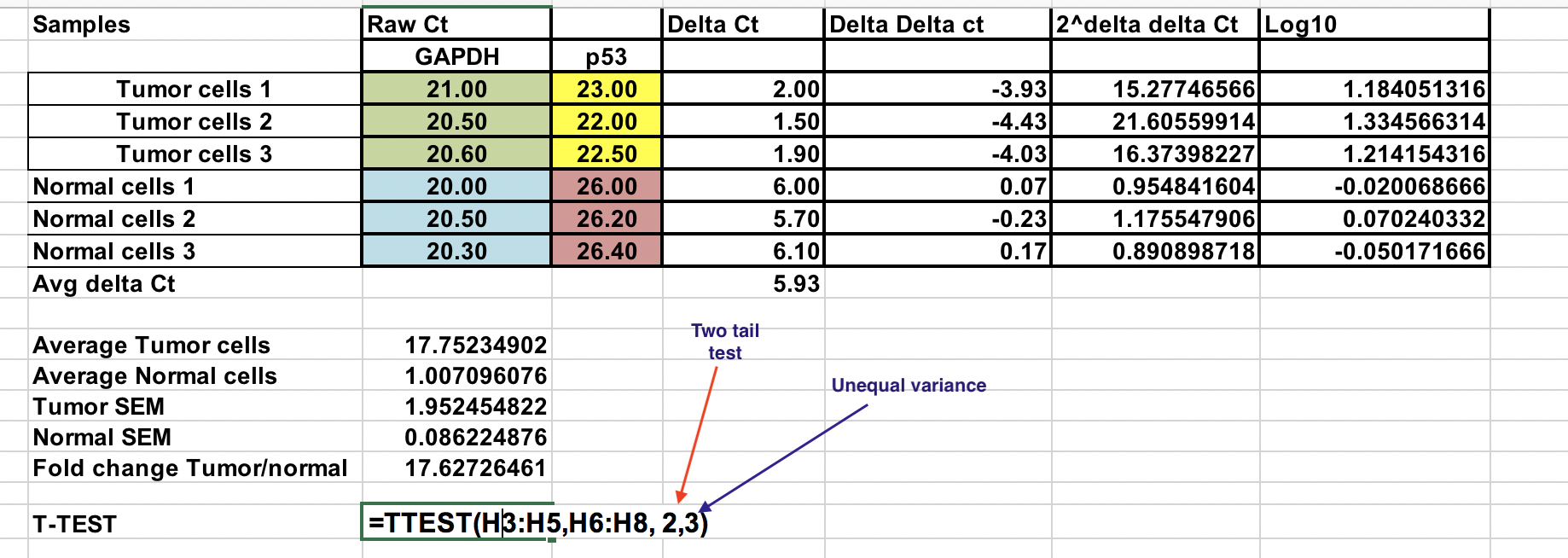
Välj log 10 av 2^-(∆∆Ct)-värden för normala och tumörprover enligt uppgift. Använd testet med två svansar (nummer 2) och anta ojämlik varians (3).
Det resulterande P-värdet är mindre än 0,05 och därför förkastar vi nollhypotesen och två medelvärden för proverna skiljer sig signifikant åt på 0,05-nivån.