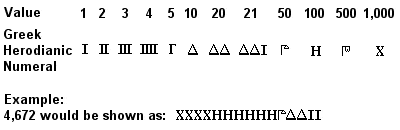
Grekiska herodianiska siffror
I takt med att det grekiska imperiet började sprida sitt inflytande till Mindre Asien, Mesopotamien och vidare var grekerna smarta nog att anta och anpassa användbara element från de samhällen de erövrade. Detta gällde lika mycket för deras matematik som för något annat, och de adopterade delar av matematiken från både babylonierna och egyptierna. Men de började snart göra viktiga bidrag på egen hand och för första gången kan vi erkänna enskilda individers bidrag. Under den hellenistiska perioden hade grekerna lett en av de mest dramatiska och viktiga revolutionerna i det matematiska tänkandet genom tiderna.
Attiska eller herodiska siffror
Det antika grekiska siffersystemet, känt som attiska eller herodiska siffror, var fullt utvecklat omkring 450 f.v.t., och i regelbunden användning möjligen så tidigt som på 700-talet f.v.t. Det var ett system med bas 10 som liknade det tidigare egyptiska systemet (och ännu mer liknade det senare romerska systemet), med symboler för 1, 5, 10, 50, 100, 500 och 1 000 som upprepades så många gånger som behövdes för att representera det önskade talet. Addition skedde genom att man summerade separat symbolerna (1:or, 10:or, 100:or osv.) i de tal som skulle adderas, och multiplikation var en mödosam process som byggde på successiva fördubblingar (division byggde på det omvända av denna process).
Thales’ interceptsats
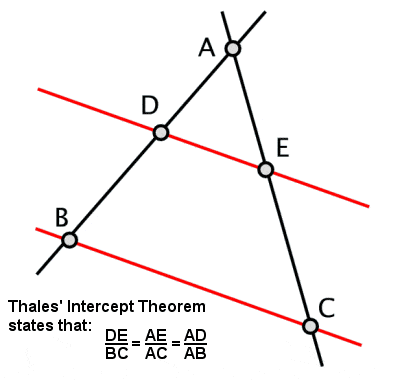
Thales’ interceptsats
Men det mesta av den grekiska matematiken byggde på geometri. Thales, en av det antika Greklands sju vise, som levde på den joniska kusten i Mindre Asien under första hälften av 600-talet f.Kr., brukar anses ha varit den förste som fastställde riktlinjer för geometrins abstrakta utveckling, även om det vi känner till om hans arbete (t.ex. om likadana och rätvinkliga trianglar) nu verkar ganska elementärt.
Thales fastställde vad som har blivit känt som Thales’ sats, enligt vilken om en triangel ritas inom en cirkel med långsidan som cirkelns diameter, så kommer den motsatta vinkeln alltid att vara en rät vinkel (liksom några andra relaterade egenskaper som härletts från detta). Han tillskrivs också en annan sats, även känd som Thales’ sats eller Intercept Theorem, om förhållandet mellan de linjesegment som skapas om två skärande linjer skärs av ett par paralleller (och, i förlängningen, förhållandet mellan sidorna i likartade trianglar).
I viss mån har dock legenden om matematikern Pythagoras av Samos från 600-talet f.Kr. blivit synonymt med den grekiska matematikens födelse. Han tros faktiskt ha myntat både orden ”filosofi” (”kärlek till visdom”) och ”matematik” (”det man lär sig”). Pythagoras var kanske den förste som insåg att det gick att konstruera ett komplett matematiskt system där geometriska element motsvarade siffror. Pythagoras’ sats (eller Pythagoras’ sats) är en av de mest kända av alla matematiska satser. Men han förblir en kontroversiell figur, som vi kommer att se, och den grekiska matematiken var ingalunda begränsad till en enda man.
Tre geometriska problem
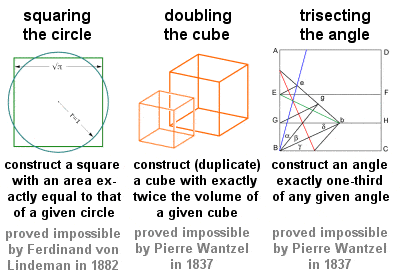
De tre klassiska problemen
Tre geometriska problem i synnerhet, som ofta kallas de tre klassiska problemen, och som alla ska lösas med rent geometriska medel med hjälp av endast en raksträcka och en kompass, går tillbaka till den grekiska geometrins tidigaste dagar: ”kvadrering (eller kvadratur) av cirkeln”, ”fördubbling (eller duplicering) av kuben” och ”tredelning av en vinkel”. Dessa obotliga problem hade ett stort inflytande på den framtida geometrin och ledde till många fruktbara upptäckter, även om deras faktiska lösningar (eller, som det visade sig, bevisen på att de var omöjliga) fick vänta till 1800-talet.
Hippokrates från Chios (inte att förväxla med den store grekiske läkaren Hippokrates från Kos. En detaljerad biografi finns här.) var en sådan grekisk matematiker som ägnade sig åt dessa problem under det femte århundradet före Kristus (hans bidrag till problemet med ”kvadrering av cirkeln” är känt som Hippokrates’ Lune). Hans inflytelserika bok ”The Elements”, som dateras till omkring 440 f.Kr., var den första sammanställningen av geometrins element, och hans arbete var en viktig källa för Euklides senare arbete.
Zenos paradox om Akilles och sköldpaddan
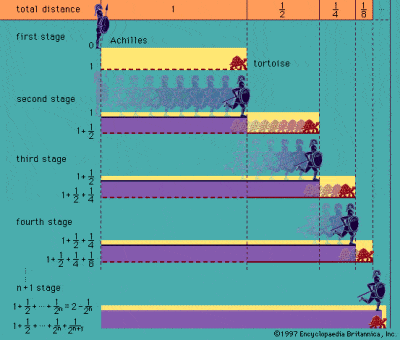
Zenos paradox om Akilles och sköldpaddan
Det var grekerna som först kämpade med idén om oändlighet, som den som beskrivs i de välkända paradoxerna som tillskrivs filosofen Zeno av Elea på 500-talet f.Kr. Den mest kända av hans paradoxer är den om Akilles och sköldpaddan, som beskriver en teoretisk tävling mellan Akilles och en sköldpadda. Akilles ger den mycket långsammare sköldpaddan ett försprång, men när Akilles når sköldpaddans startpunkt har sköldpaddan redan gått före. När Akilles når den punkten har sköldpaddan gått vidare igen, osv, osv, så att den snabba Akilles i princip aldrig kan komma ikapp den långsamma sköldpaddan.
Paradoxer som denna och Zenos så kallade dikotomiparadox bygger på rummets och tidens oändliga delbarhet och vilar på idén att en halv plus en fjärdedel plus en åttondel plus en sextondel, osv, osv, i oändlighet aldrig riktigt kommer att bli lika med en helhet. Paradoxen beror dock på det felaktiga antagandet att det är omöjligt att slutföra ett oändligt antal diskreta streck på en ändlig tid, även om det är ytterst svårt att slutgiltigt bevisa denna felaktighet. Den gamle greken Aristoteles var den förste av många som försökte motbevisa paradoxerna, särskilt eftersom han var fast övertygad om att oändligheten alltid bara kunde vara potentiell och inte verklig.
Demokrit, som är mest känd för sina förutseende idéer om att all materia består av små atomer, var också en pionjär inom matematik och geometri på 500-400-talet f.Kr. och han producerade verk med titlar som ”On Numbers”, ”On Geometrics”, ”On Tangencies”, ”On Mapping” och ”On Irrationals”, även om dessa verk inte har överlevt. Vi vet dock att han var en av de första som observerade att en kon (eller pyramid) har en tredjedel av volymen hos en cylinder (eller prisma) med samma bas och höjd, och han är kanske den förste som på allvar funderade på att dela in föremål i ett oändligt antal tvärsnitt.
Det är dock säkert sant att särskilt Pythagoras i hög grad påverkade dem som kom efter honom, däribland Platon, som grundade sin berömda akademi i Aten 387 f.v.t., och hans skyddsling Aristoteles, vars arbete om logik betraktades som slutgiltigt i över tvåtusen år. Matematikern Platon är mest känd för sin beskrivning av de fem platonska soliderna, men värdet av hans arbete som lärare och popularisatör av matematiken kan inte överskattas.
Platons elev Eudoxus av Cnidus brukar tillskrivas det första genomförandet av ”utmattningsmetoden” (som senare utvecklades av Archimedes), en tidig metod för integrering genom successiva approximationer som han använde för att beräkna volymen av pyramiden och konen. Han utvecklade också en allmän teori om proportioner, som var tillämplig på inkommensurabla (irrationella) storheter som inte kan uttryckas som ett förhållande mellan två hela tal, liksom på kommensurabla (rationella) storheter, vilket utvidgade Pythagoras’ ofullständiga idéer.
Det kanske viktigaste enskilda bidraget från grekerna – och Pythagoras, Platon och Aristoteles var alla inflytelserika i detta avseende – var dock idén om bevis och den deduktiva metoden där man använder logiska steg för att bevisa eller motbevisa satser från ursprungliga antagna axiom. Äldre kulturer, som egyptierna och babylonierna, hade förlitat sig på induktivt resonemang, dvs. att använda upprepade observationer för att fastställa tumregler. Det är detta koncept med bevis som ger matematiken dess kraft och garanterar att bevisade teorier är lika sanna i dag som för tvåtusen år sedan, och som lade grunden för Euklides och hans efterföljares systematiska sätt att se på matematiken.
| << Tillbaka till egyptisk matematik | Framåt till Pythagoras >> |