Chemguide: Stöd för CIE A level Chemistry
Lärandemål 11.2(f)
Detta påstående handlar om fördelningskoefficienter.
Innan du fortsätter bör du hitta och läsa påståendet i din kopia av kursplanen.
Partition
Om du har två icke blandbara vätskor som eter och vatten och skakar dem i en separeringstratt bildar de uppenbarligen två lager. Etern är mindre tät än vatten och bildar därför det översta lagret.
Antag nu att du skakar upp en blandning av eter och vatten som innehåller ett ämne som är lösligt i båda. Låt oss anta att ämnet, X, är mer lösligt i eter än i vatten.
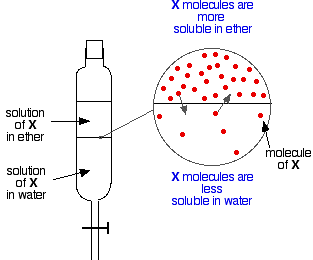
Partiklar av X kommer att korsa gränsen mellan de två vätskeskikten, och du kommer snart att få en dynamisk jämvikt upprättad. För varje partikel som rör sig in i det översta lagret kommer en partikel att röra sig tillbaka ner i det nedersta.
Du skulle kunna skriva en ekvation för detta:
. . . och precis som med alla andra jämvikter kan du hitta en jämviktskonstant:
Denna jämviktskonstant kallas för fördelningskoefficienten och ges ofta symbolen Kpc.
Som andra jämviktskonstanter är fördelningskoefficienter konstanta vid en konstant temperatur, men de har också några andra begränsningar. De fungerar bara korrekt för ganska utspädda lösningar, och lösningsmedlet måste vara i samma kemiska form i båda lösningsmedlen. Den får inte reagera, joniseras eller associera (förenas till exempel i dimerer).
Beräkningar av fördelningskoefficienter
En anmärkning om enheter
Bemärk att fördelningskoefficienten är ett enkelt förhållande mellan två koncentrationer. Det spelar ingen roll vilka koncentrationsenheter du använder – så länge du använder samma enheter upptill och nedtill.
Du kan använda mol dm-3, men oftare använder du g cm-3 – gram per kubikcentimeter.
Tekniskt sett kan de fyrkantiga parenteserna endast användas för koncentration i mol dm-3, men i Application Support Booklet och CIE:s betygsscheman används de båda för andra enheter också.
Jag är inte beredd att göra det och ska därför använda uttrycket ”koncentration av X” i stället för där icke-standardiserade koncentrationsenheter används.
Beräkning av en fördelningskoefficient
När en lösning av 1,00 g X i 100 cm3 vatten skakades med 10 cm3 eter, överfördes 0,80 g X till eterskiktet. Beräkna fördelningskoefficienten för X mellan eter och vatten.
Om du ombeds att beräkna en fördelningskoefficient mellan två lösningsmedel går koncentrationen av det först nämnda lösningsmedlet upp i Kpc-uttrycket. Så i det här fallet:
Du har tillräckligt med information för att beräkna båda koncentrationerna i g cm-3.
Koncentrationen av X i eter = 0,80/10 g cm-3
Om 0,80 g skulle överföras till etern, blir 1,00 – 0,80 g = 0.20 g kvar i vattnet.
koncentration av X i vatten = 0,20/100 g cm-3
Så:
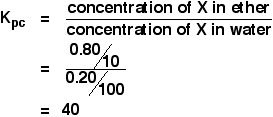
Självklart kan man räkna ut koncentrationerna i eter och i vatten som faktiska tal innan man sätter in dem i uttrycket. Gör det på det sätt du känner dig mest bekväm.
Partitionskoefficienter som denna har inga enheter – enheterna upphäver varandra eftersom de är samma upptill och nedtill.
Beräkningar som involverar fördelningskoefficienter
I CIE:s kursplan står det uttryckligen att du ska kunna beräkna en fördelningskoefficient (med andra ord, det som vi just har gjort). Den säger ingenting alls om att använda dem för att beräkna andra saker. Dessa extra beräkningar diskuteras i Application Support Booklet och har ställts två gånger i prov fram till juni 2013 (båda år 2009).
Kursboken innehåller dem inte (helt korrekt!) eftersom kursplanen inte nämner dem, och denna bok har godkänts av CIE:s examinatorer som en ”fullständig och exakt täckning” av kursplanen. Betyder det att CIE inte kommer att ställa fler frågor i framtiden? Räkna inte med det!
Ett grundläggande exempel
Vi kommer att använda samma fall som tidigare – samma lösningsmedel, samma X och samma fördelningskoefficient som vi just har beräknat.
Denna gång ska vi räkna ut hur mycket som skulle ha extraherats till eterskiktet om vi hade skakat den ursprungliga lösningen på 1,00 g X i 100 cm3 vatten med bara 5 cm3 eter.
Vi försöker räkna ut massan av X som extraherats. Låt oss kalla det m.
Utarbeta nu ett uttryck för koncentrationen av lösningen av X i eter.
koncentration av X i eter = m/5 g cm-3
Hur är det med vattnet? Det kommer att finnas (1,00 – m) g X kvar i vattnet. Så:
koncentration av X i vatten = (1,00 – m)/100 g cm-3
Nu kan du sätta in allt detta i fördelningskoefficientens uttryck. Kom ihåg att vi redan har beräknat fördelningskoefficienten för X mellan eter och vatten till 40.
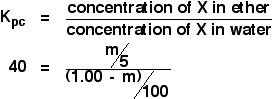
Du står då bara inför en enkel, men något tråkig, bit algebra:
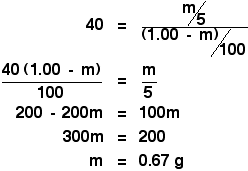
Det blir ännu tråkigare!
I den ursprungliga beräkningen för att hitta fördelningskoefficienten fick du veta att om du skakade den ursprungliga lösningen på 1,00 g X i 100 cm3 vatten med 10 cm3 eter, så extraherade du 0,80 g X.
Om du skakade den med 5 cm3 eter har vi just räknat ut att du skulle extrahera 0,67 g X.
Det skulle lämna 0,33 g X kvar i de 100 cm3 vattnet. Anta att du försiktigt hade behållit denna lösning och sedan skakat den med ytterligare en ny 5 cm3 eter.
Hur mycket X skulle du totalt utvinna genom att använda etern som två separata partier om 5 cm3 i stället för de 10 cm3 i ett svep?
Låt oss kalla massan av X som extraherats genom den andra omgången eter för n – så att vi inte blir förvirrade.
Utforma ett uttryck för koncentrationen av lösningen av X i eter.
koncentration av X i eter = n/5 g cm-3
Hur är det med vattnet? Det kommer att finnas (0,33 – n) g X kvar i vattnet efter den andra extraktionen. Så:
koncentration av X i vatten = (0,33 – n)/100 g cm-3
Nu kan du sätta in allt detta i fördelningskoefficientuttrycket för X mellan eter och vatten som tidigare.
Detta innebär att om du skulle kombinera de två 5 cm3 partierna eter skulle du ha extraherat totalt 0,67 + 0,22 g X. Det är 0.89 g.
Du fick ursprungligen veta att om du bara hade gjort detta en gång, genom att använda etern som ett enda parti på 10 cm3, skulle du bara ha extraherat 0,80 g.
Du får en effektivare extraktion genom att dela upp lösningsmedlet i mindre volymer som ovan.
Den här typen av teknik använder du vid framställningen av vissa organiska föreningar. Du extraherar det du försöker göra från någon rörig lösning i vatten så att det hamnar i ett organiskt lösningsmedel. Man tar sedan bort lösningsmedlet genom noggrann destillation.
CIE ställde en fråga som liknar denna i juni 2009 paper 4 Q8. Du var tvungen att beräkna ett värde för fördelningskoefficienten och sedan använda den i en tvåstegsextraktion precis som ovan. Beräkningen var värd 4 poäng. Detta kan vara tråkigt och (bortsett från beräkningen av fördelningskoefficienten) inte i kursplanen, men du har inte råd att inte kunna göra det.
