Kontrollsystem – blockdiagram

Blockdiagram består av ett enda block eller en kombination av block. Dessa används för att representera kontrollsystemen i bildform.

Baselement i blockdiagram

De grundläggande elementen i ett blockdiagram är ett block, summeringspunkten och startpunkten. Låt oss betrakta blockdiagrammet för ett regleringssystem med sluten krets enligt följande figur för att identifiera dessa element.

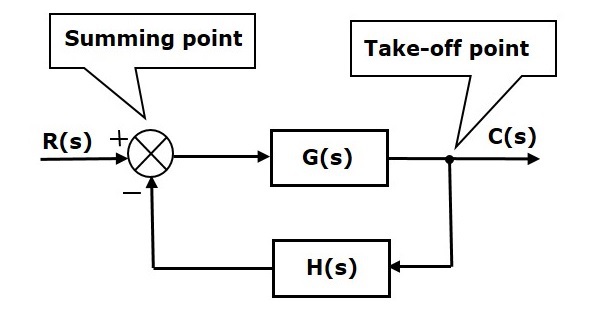
Blockdiagrammet ovan består av två block som har överföringsfunktionerna G(s) och H(s). Det har också en summeringspunkt och en startpunkt. Pilarna anger riktningen för signalflödet. Låt oss nu diskutera dessa element ett efter ett.

Block

Överföringsfunktionen för en komponent representeras av ett block. Blocket har en enda ingång och en enda utgång.

Följande figur visar ett block med ingång X(s), utgång Y(s) och överföringsfunktionen G(s).

Transferfunktion,$G(s)=\frac{Y(s)}{X(s)}$

$$$\Rightarrow Y(s)=G(s)X(s)$$

Blockets utgång erhålls genom att blockets transferfunktion multipliceras med ingången.

Summeringspunkten

Summeringspunkten representeras av en cirkel med ett kryss (X) inuti. Den har två eller flera ingångar och en enda utgång. Den producerar den algebraiska summan av ingångarna. Den utför också summering eller subtraktion eller en kombination av summering och subtraktion av ingångarna baserat på ingångarnas polaritet. Låt oss se dessa tre operationer en efter en.

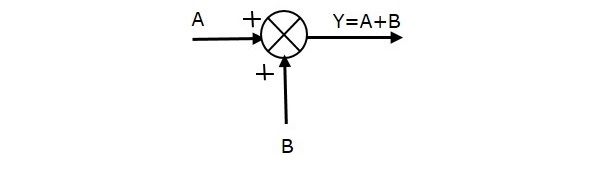
Följande figur visar summeringspunkten med två ingångar (A, B) och en utgång (Y). Här har ingångarna A och B ett positivt tecken. Så summeringspunkten ger resultatet Y som summan av A och B.

Det vill säga Y = A + B.

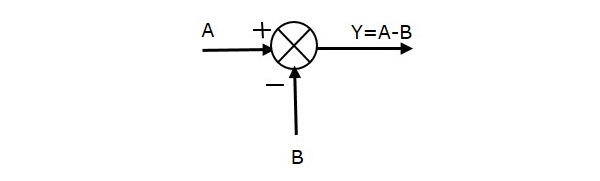
Följande figur visar summeringspunkten med två ingångar (A, B) och ett resultat (Y). Här har ingångarna A och B motsatta tecken, dvs. A har positivt tecken och B negativt tecken. Så summeringspunkten producerar utgången Y som skillnaden mellan A och B.

Y = A + (-B) = A – B.

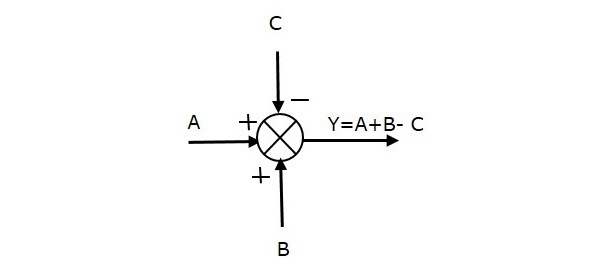
Följande figur visar summeringspunkten med tre ingångar (A, B, C) och en utgång (Y). Här har ingångarna A och B positiva tecken och C negativa tecken. Så summeringspunkten producerar utgången Y som

Y = A + B + (-C) = A + B – C.

Take-off Point

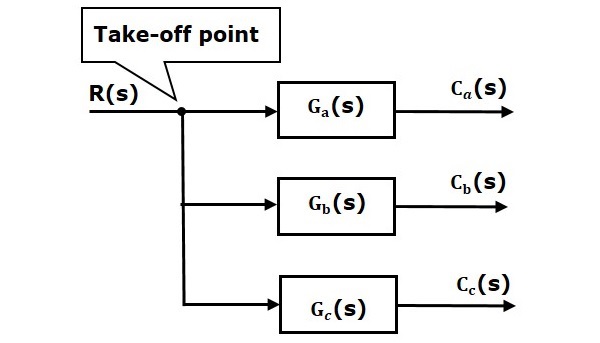
Take-off Point är en punkt från vilken samma ingångssignal kan passera genom mer än en gren. Det innebär att vi med hjälp av avtagspunkten kan tillämpa samma ingång på ett eller flera block, summeringspunkter.

I följande figur används avtagspunkten för att ansluta samma ingång, R(s), till ytterligare två block.

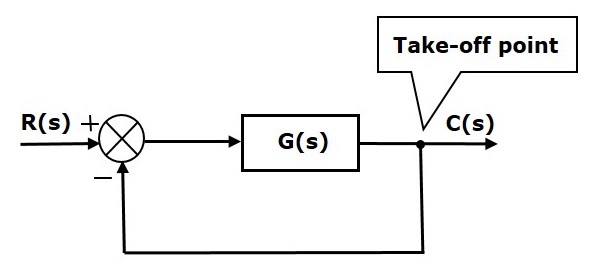
I följande figur används avtagspunkten för att ansluta utgången C(s), som en av ingångarna till summeringspunkten.

Blockdiagramrepresentation av elektriska system

I detta avsnitt ska vi representera ett elektriskt system med ett blockdiagram. Elektriska system innehåller huvudsakligen tre grundläggande element – motstånd, induktor och kondensator.

Den här bilden visar en serie RLC-krets som visas i följande figur. Där Vi(t) och Vo(t) är ingångs- och utgångsspänningarna. Låt i(t) vara den ström som passerar genom kretsen. Denna krets är i tidsdomän.

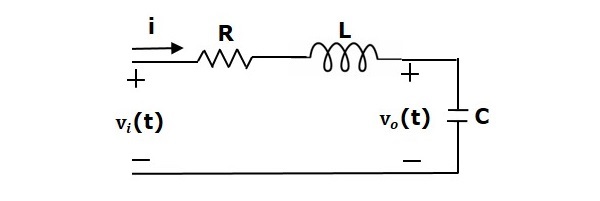
Genom att tillämpa Laplacetransformationen på denna krets får man kretsen i s-domän. Kretsen är som visas i följande figur.

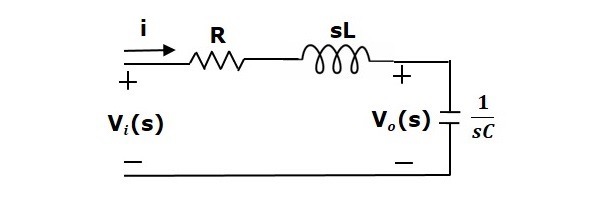
Från ovanstående krets kan vi skriva

$$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$$

$\Rightarrow I(s)=\left \{ \frac{1}{R+sL} \right \}\left \{ V_i(s)-V_o(s) \right \}$ (Ekvation 1)

$V_o(s)=\left ( \frac{1}{sC} \right )I(s)$ (Ekvation 2)

Låt oss nu rita blockdiagrammen för dessa två ekvationer individuellt. Och kombinera sedan dessa blockdiagram på rätt sätt för att få det övergripande blockdiagrammet för serien av RLC-kretsen (s-domän).

Ekvation 1 kan implementeras med ett block som har överföringsfunktionen $\frac{1}{R+sL}$. Ingång och utgång för detta block är $\left \{ V_i(s)-V_o(s) \right \}$ och $I(s)$. Vi behöver en summeringspunkt för att få $\left \{ V_i(s)-V_o(s) \right \}$. Blockdiagrammet för ekvation 1 visas i följande figur.

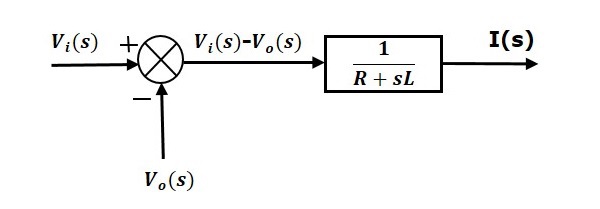
Ekvation 2 kan genomföras med ett block som har överföringsfunktionen $\frac{1}{sC}$. Ingången och utgången för detta block är $I(s)$ och $V_o(s)$. Blockdiagrammet för ekvation 2 visas i följande figur.

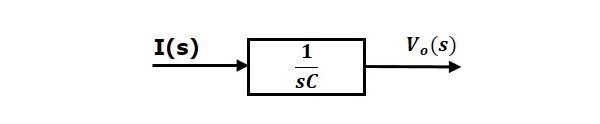
Det övergripande blockdiagrammet för serien av RLC-kretsen (s-domän) visas i följande figur.

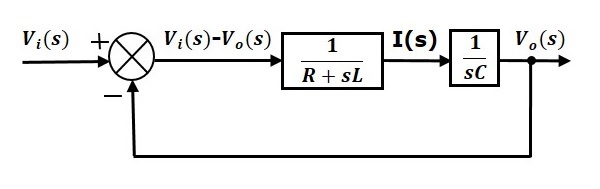
På samma sätt kan du rita blockdiagrammet för vilken elektrisk krets eller vilket elektriskt system som helst bara genom att följa denna enkla procedur.

• Konvertera den elektriska kretsen i tidsdomän till en elektrisk krets i s-domän genom att tillämpa Laplacetransformen.

• Skriv ner ekvationerna för strömmen som passerar genom alla serieförgreningar och spänningen över alla shuntförgreningar.

• Rita blockdiagrammen för alla ovanstående ekvationer individuellt.

• Kombinera alla dessa blockdiagram på rätt sätt för att få det övergripande blockdiagrammet för den elektriska kretsen (s-domän).