Toteutus
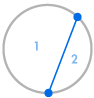
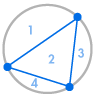
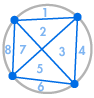
Kuvittele, että asetamme useita pisteitä ympyrän kehälle ja yhdistämme jokaisen pisteen toisiinsa. Tämä jakaa ympyrän moneen eri alueeseen, ja voimme laskea alueiden lukumäärän kussakin tapauksessa. Alla olevat kaaviot osoittavat, kuinka monta aluetta on useilla eri pistemäärillä ympyrän kehällä. Meidän on varmistettava, että ympyrän sisällä jokaisessa leikkauspisteessä kohtaa vain kaksi viivaa, ei kolmea tai useampaa.
 |
 |
 |
 |
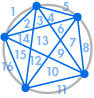 |
| 1 alue | 2 aluetta | 4 aluetta | 8 aluetta | 16 aluetta |
Voidaan heti nähdä kuvio: Alueiden määrä on aina kaksinkertainen edelliseen verrattuna, joten saamme sarjan 1, 2, 4, 8, 16, … Tämä tarkoittaa, että jos kehällä olisi 6 pistettä, olisi 32 aluetta, ja jos kehällä olisi 7 pistettä, olisi 64 aluetta.
Voisimme päättää, että olemme tyytyväisiä tähän tulokseen. Alueiden määrä on aina kaksinkertainen edelliseen verrattuna – toimiihan tämä viidessä ensimmäisessä tapauksessa. Tai saatamme päättää, että tarkistamme varmuuden vuoksi vielä muutaman:
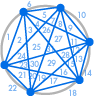 |
 |
| 31 aluetta, ei 32 | 57 aluetta, ei 64 |
Jotain on valitettavasti mennyt pieleen: 31 saattaa näyttää laskuvirheeltä, mutta 57 on paljon vähemmän kuin 64. Jakso jatkuu 99, 163, 256, …, hyvin erilaisena kuin mitä saisimme, kun kaksinkertaistaisimme edellisen luvun.
Tämä esimerkki havainnollistaa, miksi matematiikassa ei voi sanoa, että havainto on aina totta vain siksi, että se toimii muutamassa testatussa tapauksessa. Sen sijaan sinun on keksittävä tiukka looginen argumentti, joka johtaa jo tuntemistasi tuloksista johonkin uuteen, jonka haluat osoittaa olevan totta. Tällaista argumenttia kutsutaan todisteeksi.
Todisteet erottavat matematiikan kaikista muista tieteistä, sillä kun olemme todistaneet jonkin asian, olemme täysin varmoja siitä, että se on ja tulee aina olemaan totta. Se ei ole vain teoria, joka sopii havaintoihimme ja joka voidaan tulevaisuudessa korvata paremmalla teorialla.
Yllä olevassa esimerkissä voisimme laskea ympyrän sisäpuolen leikkauspisteiden lukumäärän. Pohtimalla tarkkaan leikkauspisteiden, viivojen ja alueiden lukumäärän välistä suhdetta löydämme lopulta erilaisen yhtälön alueiden lukumäärälle, kun on x = V.Axi pisteitä ympyrässä:
alueiden lukumäärä = x4 – 6 x3 + 23 x2 – 18 x + 2424 = (Math.pow(V.Axi,4) – 6*Math.pow(V.Axi,3) + 23*Math.pow(V.Axi,2) – 18*V.Axi + 24)/24.
Tämä yhtälö toimii kaikissa yllä olevissa tapauksissa. Voisimme nyt yrittää todistaa sen jokaiselle x:n arvolle käyttäen ”induktiota”, tekniikkaa, joka selitetään jäljempänä.
Traditionaalisesti todistuksen loppu merkitään ■:llä tai □:llä tai kirjoittamalla QED tai ”quod erat demonstrandum”, joka on latinaa ja tarkoittaa ”mitä piti näyttää”.
Tulosta tai havaintoa, jonka luulemme olevan totta, kutsutaan hypoteesiksi tai olettamukseksi. Kun olemme todistaneet sen, kutsumme sitä teoreemaksi. Kun olemme todistaneet teoreeman, voimme käyttää sitä todistaaksemme muita, monimutkaisempia tuloksia – rakentaen näin kasvavaa matemaattisten teoreemojen verkostoa.
Aksiomit

Raphaelin Ateenan koulu: Antiikin kreikkalaiset matemaatikot olivat ensimmäisiä, jotka lähestyivät matematiikkaa loogisen ja aksiomaattisen viitekehyksen avulla.
Yksi mielenkiintoinen kysymys on se, mistä aloittaa. Miten todistat ensimmäisen lauseen, jos et tiedä vielä mitään? Valitettavasti et voi todistaa jotain käyttämällä ei mitään. Tarvitset ainakin muutamia rakennuspalikoita, joista aloittaa, ja näitä kutsutaan aksioomeiksi.
Matemaatikot olettavat aksioomien olevan totta pystymättä todistamaan niitä. Tämä ei kuitenkaan ole niin ongelmallista kuin miltä se saattaa vaikuttaa, koska aksioomat ovat joko määritelmiä tai selvästi ilmeisiä, ja aksioomia on vain hyvin vähän. Esimerkiksi aksiooma voisi olla, että a + b = b + a mille tahansa kahdelle luvulle a ja b.
Aksioomien oikeellisuus on tärkeää, koska koko matematiikka perustuu niihin. Jos aksioomia on liian vähän, voidaan todistaa hyvin vähän ja matematiikka ei olisi kovin mielenkiintoista. Jos aksioomia on liikaa, voidaan todistaa melkein mitä tahansa, eikä matematiikka myöskään olisi kiinnostavaa. Aksioomat eivät myöskään voi olla keskenään ristiriidassa.
Matematiikassa ei ole kyse oikean aksioomajoukon valitsemisesta, vaan puitteiden kehittämisestä näistä lähtökohdista. Jos lähdet liikkeelle erilaisista aksioomista, saat erilaista matematiikkaa, mutta loogiset argumentit ovat samat. Jokaisella matematiikan osa-alueella on omat perusaksioomansa.
Kun matemaatikot ovat todistaneet lauseen, he julkaisevat sen muiden matemaatikkojen tarkistettavaksi. Joskus he löytävät virheen loogisessa väitteessä, ja joskus virhe löytyy vasta monta vuotta myöhemmin. Periaatteessa on kuitenkin aina mahdollista purkaa todistus perusaksioomiin.
joukkoteoria ja valinta-aksiooma

Todisteiden muotoilemiseksi on joskus palattava sen kielen perustaan, jolla matematiikkaa kirjoitetaan: joukko-oppiin.
Joukko on kokoelma objekteja, kuten lukuja. Joukon alkiot kirjoitetaan yleensä sulkeisiin. Voimme löytää kahden joukon liiton (niiden alkioiden joukko, jotka ovat kummassakin joukossa) tai voimme löytää kahden joukon leikkauksen (niiden alkioiden joukko, jotka ovat molemmissa joukoissa).
Monet matemaattiset ongelmat voidaan muotoilla joukko-opin kielellä, ja niiden todistamiseen tarvitsemme joukko-opin aksioomia. Matemaatikot ovat aikojen saatossa käyttäneet erilaisia aksioomakokoelmia, joista laajimmin hyväksyttyjä ovat yhdeksän Zermelo-Fraenkelin (ZF) aksioomaa:
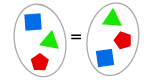
LAAJUUSAKSIOMI
Jos kahdella joukolla on samat alkioelementit, ne ovat yhtä suuria.
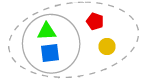
AXIOM OF SEPARATION
Voidaan muodostaa joukosta osajoukko, joka koostuu joistakin alkioista.

EMPTY SET AXIOM
On joukko, jolla ei ole jäseniä, kirjoitettuna {} tai ∅.
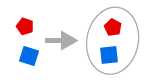
PAIKKAJÄRJESTELMIEN AXIOM
Kahdella objektilla x ja y voimme muodostaa joukon {x, y}.
YHDISTYS- AXIOM
Voidaan muodostaa kahden tai useamman joukon unioni.
POTENTIAALIJÄRJESTELMIEN AXIOMI
Voidaan muodostaa minkä tahansa joukon avulla kaikkien osajoukkojen joukko (potenssijoukko).
MÄÄRITTÄMÄTTÖMYYDEN AXIOMI
On joukko, jolla on äärettömän monta alkiota.

AXIOM OF FOUNDATION
Määrät rakentuvat yksinkertaisemmista joukoista, eli jokaisella (ei-tyhjällä) joukolla on minimijäsen.
AKSIOMI KORVAAMISESTA
Jos sovellamme funktiota joukon jokaiseen alkioon, vastaus on edelleen joukko.
Jos ajattelet joukko-oppia, useimmat näistä aksioomista tuntuvat täysin itsestäänselvyyksiltä – ja niin aksioomien kuuluukin olla. On kuitenkin kymmenes aksiooma, joka on hieman ongelmallisempi:
VALINTA-AKSIOOMI
Jos on äärettömän monta ei-tyhjää joukkoa, jokaisesta näistä joukoista voidaan valita yksi alkio.
Ensi silmäyksellä valinta-aksiooma (AC) näyttää yhtä viattomalta kuin muutkin edellä mainitut. Äärettömyyden käytöllä on kuitenkin useita odottamattomia seurauksia. AC:n avulla voidaan esimerkiksi todistaa, että on mahdollista leikata pallo viiteen osaan ja koota ne uudelleen niin, että saadaan kaksi palloa, joista kumpikin on identtinen alkuperäisen pallon kanssa. Tämä on vain teoreettinen käsite – tarvittavat palat ovat fraktaalisia, mikä tarkoittaa, että niitä ei voi todellisuudessa olla olemassa, ja jotkin paloista ovat ”ei-mitattavia”, mikä tarkoittaa, että niille ei ole määritelty tilavuutta. Mutta se, että valinta-aksioomaa voidaan käyttää näiden mahdottomien leikkausten konstruoimiseen, on varsin huolestuttavaa.
Logiikantutkijoiden keskuudessa käydään kiihkeää keskustelua siitä, pitäisikö valinta-aksiooma hyväksyä vai ei. Jokainen kokoelma aksioomia muodostaa pienen ”matemaattisen maailman”, ja eri teoreemat voivat olla totta eri maailmoissa. Kyse on oikeastaan vain siitä, oletko onnellinen siitä, että elät maailmassa, jossa voit tehdä yhdestä pallosta kaksi palloa…
Todistus induktiolla
Todistus induktiolla on tekniikka, jonka avulla voidaan todistaa, että tietty väite on tosi kaikille luonnollisille luvuille 1, 2, 3, … ”Väite” on tavallisesti yhtälö tai kaava, joka sisältää muuttujan n, joka voi olla mikä tahansa luonnollinen luku. Merkitään n:ään sovellettavaa lausumaa nimellä S(n). Seuraavassa on matemaattisen induktion neljä vaihetta:
- Ensin todistetaan, että S(1) on tosi, eli että lausuma S on tosi luvulle 1.
- Nyt oletetaan, että S(k) on tosi, eli että lausuma S on tosi jollekin luonnolliselle luvulle k.
- Tämän olettamuksen avulla yritetään päätellä, että myös S(k + 1) on tosi. Näin ollen aina kun S on tosi yhdelle luvulle, se on tosi myös seuraavalle luvulle.
- Koska tiedämme, että S(1) on tosi, S(2) täytyy olla tosi. Ja siksi S(3) on oltava tosi. Ja siksi S(4) on oltava tosi. Ja niin edelleen:

Induktiota voidaan verrata putoaviin dominopalikoihin: aina kun yksi domino putoaa, myös seuraava putoaa. Ensimmäinen askel, sen todistaminen, että S(1) on tosi, käynnistää äärettömän ketjureaktion.
Ensimmäinen askel jää usein huomiotta, koska se on niin yksinkertainen. Itse asiassa se on hyvin tärkeä ja koko induktioketju riippuu siitä – kuten muutamat seuraavista esimerkeistä osoittavat…
Hanoin tornit -pelin tavoitteena on siirtää tietty määrä kiekkoja yhdestä tapista toiseen. Voit siirtää vain yhden levyn kerrallaan, etkä saa laittaa suurempaa levyä pienemmän päälle. Yritä siirtää levytorni ensimmäisestä tapista viimeiseen tappiin mahdollisimman vähillä siirroilla:
Kiekkojen määrä: Start Over Moves: 0
Kun olemme ymmärtäneet pelisäännöt, voimme yrittää löytää vähiten tarvittavien askelten määrän, kun annamme minkä tahansa määrän kiekkoja. Edellä esitetyllä pelillä leikkimällä voimme havaita, että n kiekon kanssa tarvitaan vähintään 2n – 1 askelta. Kutsutaan tätä väittämää S(n):ksi.
S(1) on selvästi tosi, koska yhdellä levyllä tarvitaan vain yksi siirto, ja 21 – 1 = 1.
Yritetään nyt olettaa, että S(k) on tosi, eli että k levyllä tarvitaan 2k – 1 askelta. Sitten jos meillä on k + 1 levyä:
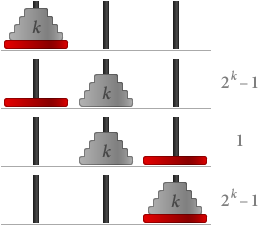
Kokonaisuudessaan tarvitsemme (2k – 1) + 1 + (2k – 1) = 2(k+1) – 1 askelta. Tämä tarkoittaa, että myös S(k + 1) on tosi.
Matemaattisen induktion avulla S(n) on tosi kaikille n:n arvoille, mikä tarkoittaa, että tehokkain tapa siirtää n = V.Hanoi-levyä vaatii 2n – 1 = Math.pow(2,V.Hanoi)-1 siirtoa. ■
Todistetaan induktion avulla, että n ensimmäisen luonnollisen luvun summa on n (n + 1)2. Tarkistetaan ensin yhtälö pienille n:n arvoille:
1 = 1 (1 + 1)2.
1 + 2 = 2 (2 + 1)2 = 3.
Seuraavaksi oletetaan, että tulos pätee k:lle, eli että 1 + 2 + … + k = k (k + 1)2, missä k on jokin luku, jota emme määritä. Nyt
1 + 2 + … + k + (k + 1) = k (k + 1)2 + (k + 1) = (k + 1) (k + 2)2 = (k + 1) 2.
Olemme juuri todistaneet, että jos yhtälö on tosi jollakin k:lla, niin se on tosi myös k + 1:llä. Matemaattisen induktion avulla yhtälö on tosi kaikille n:n arvoille. ■
On toinenkin nokkela tapa todistaa yllä oleva yhtälö, joka ei käytä induktiota. Väitetään, että Carl Friedrich Gauss (1777 – 1855), yksi historian suurimmista matemaatikoista, löysi tämän menetelmän peruskoulussa, kun hänen opettajansa pyysi häntä laskemaan yhteen kaikki kokonaisluvut 1:stä 100:aan.
Induktiota käyttäen haluamme todistaa, että kaikilla ihmisillä on sama hiusten väri. Olkoon S(n) väite, että ”missä tahansa n ihmisen ryhmässä on sama hiusväri”.
Yksiselitteisesti S(1) on tosi: missä tahansa vain yhden ihmisen ryhmässä kaikilla on sama hiusväri.
Asettakaamme nyt S(k), että missä tahansa k ihmisen ryhmässä kaikilla on sama hiusväri. Jos korvaamme jonkun ryhmän jäsenen jollakin muulla, heitä on edelleen yhteensä k ja heillä on siis sama hiusväri. Tämä toimii mille tahansa alkuryhmälle, mikä tarkoittaa, että myös kaikilla k + 1:n ryhmillä on sama hiusten väri. Siksi S(k + 1) on tosi.
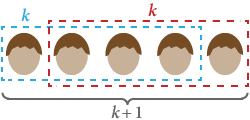
Matemaattisen induktion perusteella kaikilla ihmisillä on sama hiusväri! ■
Jotain on selvästikin mennyt pieleen yllä olevassa todistuksessa – eihän kaikilla ihmisillä ole sama hiusväri. Löydätkö virheen?
Joitakin teoreemoja ei oikein voi todistaa induktiolla – on käytettävä hieman muunneltua versiota, jota kutsutaan vahvaksi induktioksi. Sen sijaan, että olettaisimme S(k) todistaaksemme S(k + 1), oletamme kaikki S(1), S(2), … S(k) todistaaksemme S(k + 1). Kaikki, mikä voidaan todistaa (heikon) induktion avulla, voidaan selvästi todistaa myös vahvan induktion avulla, mutta ei päinvastoin.
Aritmetiikan perusteoriassa sanotaan, että kaikki kokonaisluvut, jotka ovat suurempia kuin 1, ovat joko alkulukuja, tai ne voidaan olennaisesti yksikäsitteisellä tavalla kirjoittaa alkulukujen tulona.
Voidaan todistaa osia siitä vahvan induktion avulla: Olkoon S(n) väite, että ”kokonaisluku n on alkuluku tai voidaan kirjoittaa alkulukujen tulona”. S(1) on poikkeus, mutta S(2) on selvästi tosi, koska 2 on alkuluku.
Asettakaamme nyt, että S(1), S(2), …, S(k) ovat kaikki tosi, jollekin kokonaisluvulle k. Tiedämme, että k + 1 on joko alkuluku tai että sillä on tekijöitä, jotka ovat pienempiä kuin k + 1. Oletuksemme perusteella tiedämme, että nämä tekijät voidaan kirjoittaa alkulukujen tulona. Näin ollen, ellei se ole alkuluku, k + 1 voidaan myös kirjoittaa alkulukujen tulona. Tämä tarkoittaa, että S(k + 1) on tosi.
Vahvan induktion avulla S(n) on tosi kaikille luvuille n, jotka ovat suurempia kuin 1. ■
Sen todistaminen, että tämä alkulukujen kertolasku on ainutkertainen (ellei lasketa tekijöiden eri järjestyksiä), vaatii enemmän työtä, mutta ei ole erityisen vaikeaa.
Vaikuttaa siltä, että heikon induktion periaate ja vahvan induktion periaate ovat ekvivalentteja: kumpikin implikoi toisensa. Molemmat ovat myös ekvivalentteja kolmannen lauseen, hyvinjärjestysperiaatteen, kanssa: millä tahansa (ei-tyhjällä) luonnollisten lukujen joukolla on minimaalinen alkio, joka on pienempi kuin kaikki muut.
Hyvinjärjestysperiaate on luonnollisten lukujen määrittelevä ominaisuus. Se on yksi perusaksioomista, joita käytetään luonnollisten lukujen ![]() = {1, 2, 3, …} määrittelyssä. Näitä aksioomeja kutsutaan Peanon aksioomeiksi, jotka on nimetty italialaisen matemaatikon Guiseppe Peanon (1858 – 1932) mukaan.
= {1, 2, 3, …} määrittelyssä. Näitä aksioomeja kutsutaan Peanon aksioomeiksi, jotka on nimetty italialaisen matemaatikon Guiseppe Peanon (1858 – 1932) mukaan.
Todistaminen ristiriidalla
Todistaminen ristiriidalla on toinen tärkeä todistustekniikka. Jos haluamme todistaa väitteen S, oletamme, että S ei ollut totta. Tämän oletuksen avulla yritämme päätellä väärän tuloksen, kuten 0 = 1. Jos kaikki vaiheemme olivat oikein ja tulos on väärä, alkuperäisen oletuksemme on täytynyt olla väärä. Alkuperäinen olettamuksemme oli, että S ei ole tosi, mikä tarkoittaa, että S on itse asiassa tosi.
Tätä tekniikkaa voidaan käyttää monissa eri tilanteissa, kuten todistettaessa, että √2 on irrationaalinen, todistettaessa, että reaaliluvut ovat lukemattomia, tai todistettaessa, että alkulukuja on äärettömän monta.
Tässä on toinen hauska esimerkki:
Voidaan käyttää ristiriitaisuustodistusta yhdessä hyvien järjestysten periaatteen kanssa todistaaksemme, että kaikki luonnolliset luvut ovat ”kiinnostavia”.
Esitettäköön, että kaikki luonnolliset luvut eivät ole kiinnostavia, ja olkoon S ei-kiinnostavien lukujen joukko. Hyvinjärjestysperiaatteen mukaan S:llä on pienin jäsen x, joka on pienin ei-kiinnostava luku. Tämä kummallinen ominaisuus tekee x:stä selvästi erityisen mielenkiintoisen luvun. Tämä on ristiriita, koska oletimme, että x on ei-kiinnostava.
Siten kaikki luvut ovat kiinnostavia. ■
Gödel ja todistamattomat lauseet

Kurt Gödel (1906-1978)
Matematiikka alkoi 1900-luvun alkupuolella kasvaa nopeasti, ja tuhannet matemaatikot työskentelivät lukemattomilla uusilla aloilla. David Hilbert (1862-1943) käynnisti laajan ohjelman matematiikan formalisoimiseksi ja matematiikan perusteiden epäjohdonmukaisuuksien ratkaisemiseksi. Siihen kuului kaikkien teoreemojen todistaminen yksinkertaisten ja universaalien aksioomien avulla, sen todistaminen, että tämä aksioomien joukko on johdonmukainen, ja sen todistaminen, että tämä aksioomien joukko on täydellinen eli että kaikki matemaattiset lausumat voidaan todistaa tai kumota aksioomien avulla.
Valitettavasti Kurt Gödel tuhosi nämä suunnitelmat vuonna 1931. Hän osoitti, että missä tahansa (riittävän monimutkaisessa) matemaattisessa järjestelmässä, jossa on tietty joukko aksioomia, voidaan löytää joitakin lausumia, joita ei voida todistaa eikä kumota näiden aksioomien avulla. Ei myöskään ole mahdollista todistaa, että tietty joukko aksioomia on johdonmukainen, käyttämällä mitään muuta kuin itse aksioomia.
Gödelin löytö perustuu siihen, että aksioomien joukon avulla ei voi sanoa mitään itsestään, kuten onko se johdonmukainen. Ongelmia itseensä viittaamisen kanssa ei löydy vain matematiikasta vaan myös kielestä. Tässä on valehtelijan paradoksi:
”Tämä lause on väärä.”
Yllä oleva lause yrittää sanoa jotain itsestään. Jos se on totta, lause kertoo meille, että se on väärä. Jos se on väärä, niin lause kertoo meille, että se ei ole väärä, eli että se on tosi. Itse asiassa lause ei ole sen enempää tosi kuin epätosi.
Kun Gödelin lauseet julkaistiin ensimmäisen kerran, ne huolestuttivat syvästi monia matemaatikkoja. Kun lähdetään todistamaan havaintoa, ei tiedetä, onko todistus olemassa – tulos saattaa olla tosi mutta todistamaton. Nykyään tiedämme, että epätäydellisyys on perustavanlaatuinen osa paitsi logiikkaa myös tietotekniikkaa, joka perustuu loogisia operaatioita suorittaviin koneisiin.
Yllättäen on mahdollista todistaa, että tietyt lausumat ovat todistamattomia. Yksi esimerkki on jatkumohypoteesi, joka koskee äärettömien joukkojen kokoa.
Kurt Gödelille kehittyi elämänsä loppupuolella vakavia mielenterveysongelmia, ja hän kuoli itsensä nälkään vuonna 1978. Hänen oivalluksensa logiikan perusteista olivat syvällisimpiä sitten antiikin kreikkalaisten kehittämän todistamisen.