
Bertrand Russell (1872-1970) ja A.N. Whitehead (1861-1947)
Bertrand Russell ja Alfred North Whitehead olivat brittiläisiä matemaatikkoja, loogikkoja ja filosofeja, jotka kuuluivat 1900-luvun alkupuolella mannermaista idealismia vastustaneen brittiläisen kapinan etujoukkoon, ja he tekivät keskenään merkittävän panoksen matemaattisen logiikan ja joukkojen teorian aloille.
Whitehead oli näistä kahdesta vanhempi, ja hän oli lähtöisin puhtaammasta matemaattisuudesta. Hänestä tuli Russellin opettaja Cambridgen Trinity Collegessa 1890-luvulla, ja sitten hän teki 1900-luvun ensimmäisellä vuosikymmenellä yhteistyötä kuuluisamman entisen oppilaansa kanssa heidän monumentaalisen teoksensa ”Principia Mathematica” parissa. Ensimmäisen maailmansodan jälkeen, josta Russell vietti suuren osan vankilassa pasifistisen toimintansa vuoksi, yhteistyö kuitenkin hiipui, ja Whiteheadin akateeminen ura jäi sen jälkeen räikeämmän Russellin varjoon. Hän muutti Yhdysvaltoihin 1920-luvulla ja vietti siellä loppuelämänsä.
Russell syntyi varakkaaseen brittiläiseen aristokratiaperheeseen, vaikka hänen vanhempansa olivatkin aikaansa nähden äärimmäisen liberaaleja ja radikaaleja. Hänen vanhempansa kuolivat Russellin ollessa melko nuori, ja Russellin kasvatti pitkälti hänen vakaumuksellisen viktoriaaninen (joskin varsin edistyksellinen) isoäitinsä. Hänen nuoruutensa oli hyvin yksinäistä, ja hän kärsi masennuksesta ja väitti myöhemmin, että vain hänen rakkautensa matematiikkaan esti häntä tekemästä itsemurhaa. Hän opiskeli matematiikkaa ja filosofiaa Cambridgen yliopistossa G. E. Mooren ja A. N. Whiteheadin johdolla ja kehittyi siellä innovatiiviseksi filosofiksi, tuotteliaaksi kirjailijaksi monista aiheista, vakaumukselliseksi ateistiksi ja innostuneeksi matemaatikoksi ja loogikoksi. Nykyään häntä pidetään yhtenä analyyttisen filosofian perustajista, mutta hän kirjoitti lähes jokaisesta tärkeästä filosofian osa-alueesta, erityisesti metafysiikasta, etiikasta, epistemologiasta, matematiikan filosofiasta ja kielifilosofiasta.
Russell oli koko pitkän elämänsä ajan vannoutunut ja korkean profiilin poliittinen aktivisti. Hän oli näkyvä sodanvastainen aktivisti sekä ensimmäisen että toisen maailmansodan aikana, puolusti vapaakauppaa ja anti-imperialismia, ja myöhemmin hänestä tuli jyrkkä kampanjoija ydinaseriisunnan ja sosialismin puolesta sekä Adolf Hitleriä, Neuvostoliiton totalitarismia ja Yhdysvaltojen osallistumista Vietnamin sotaan vastaan.
Russellin paradoksi
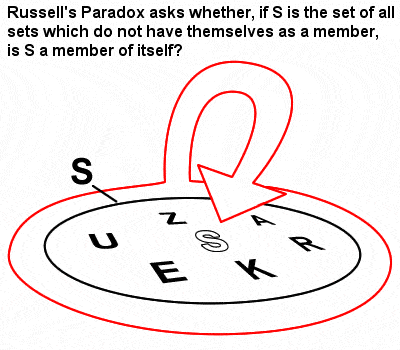
Russellin paradoksi
Russellin matematiikkaan vaikutti suuresti joukko-oppi ja logiikkateoria, joita Gottlob Frege oli kehittänyt Cantorin uraauurtavan varhaisen joukkorakennetyöskentelyn seurauksena. Vuonna 1903 ilmestyneessä teoksessaan ”The Principles of Mathematics” (Matematiikan periaatteet) hän kuitenkin havaitsi Russellin paradoksina tunnetun asian (joukko, joka sisältää joukkoja, jotka eivät ole itsensä jäseniä), joka osoitti, että Fregen naiivi joukko-oppi saattoi itse asiassa johtaa ristiriitaisuuksiin.
Paradoksia havainnollistetaan toisinaan seuraavalla yksinkertaistetulla esimerkillä: ”Jos parturi ajelee kaikki ja vain ne kylän miehet, jotka eivät ajele itseään, ajeleeko hän itseään?”
Paradoksi näytti viittaavan siihen, että koko matematiikan perusteisiin ei voitu enää luottaa ja että edes matematiikassa totuutta ei voitu koskaan tietää absoluuttisesti (Gödelin ja Turingin myöhemmät työt vain pahensivat tätä). Russellin kritiikki riitti horjuttamaan Fregen luottamusta koko logiikan rakennelmaan, ja hän oli niin armollinen, että myönsi tämän avoimesti ”Aritmetiikan peruslakien” niteen II hätäisesti kirjoitetussa liitteessä.
Mutta Russellin pääteos oli monoliittinen ”Principia Mathematica”, joka julkaistiin kolmessa niteessä vuosina 1910, 1912 ja 1913. Ensimmäisen niteen kirjoitti yhdessä Whitehead, vaikka kaksi myöhempää olivatkin lähes kokonaan Russellin työtä. Tämän kunnianhimoisen teoksen tavoitteena ei ollut vähempää kuin pyrkimys johtaa koko matematiikka puhtaasti loogisista aksioomista välttäen samalla sellaisia paradokseja ja ristiriitoja, joita Fregen aiemmissa joukko-opin teoksissa esiintyi. Russell saavutti tämän käyttämällä ”tyyppien” teoriaa tai järjestelmää, jossa jokaiselle matemaattiselle oliolle määritetään tyyppi tyyppien hierarkiassa siten, että tietyn tyypin objektit muodostetaan yksinomaan hierarkiassa alempana olevien edeltävien tyyppien objekteista, mikä estää silmukoiden syntymisen. Kukin elementtien joukko on siis eri tyyppiä kuin kukin sen elementti, joten ei voida puhua ”kaikkien joukkojen joukosta” tai vastaavista konstruktioista, jotka johtavat paradokseihin.
”Principia” vaati kuitenkin tyyppiteorian perusaksioomien lisäksi kolme muuta aksioomaa, jotka eivät näyttäneet pitävän paikkaansa pelkkinä logiikan asioina, nimittäin ”äärettömyyden aksiooman” (joka takaa vähintään yhden äärettömän joukon, nimittäin kaikkien luonnollisten lukujen joukon, olemassaolon), ”valinnan aksiooman” (joka takaa, että annettuna mikä tahansa kokoelma ”säiliöitä”, joka sisältää vähintään yhden objektin, on mahdollista valita täsmälleen yksi objekti kustakin säiliöstä, vaikka säiliöitä olisi äärettömän monta, ja että ei ole olemassa mitään ”sääntöä” sille, mikä objekti kustakin säiliöstä valitaan) ja Russellin oma ”redusoitavuuden aksiooma” (joka sanoo, että mikä tahansa propositionaalinen totuusfunktio voidaan ilmaista muodollisesti ekvivalentilla predikatiivisella totuusfunktiolla).
Noin kymmenen vuoden aikana, jotka Russell ja Whitehead viettivät ”Principia”-teoksen parissa, luonnos toisensa jälkeen aloitettiin ja hylättiin, kun Russell jatkuvasti mietti uudelleen perusoletuksiaan. Russell ja hänen vaimonsa Alys jopa muuttivat Whiteheadien luo työn vauhdittamiseksi, vaikka hänen oma avioliittonsa kärsi, kun Russell ihastui Whiteheadin nuoreen vaimoon Evelyniin. Lopulta Whitehead vaati teoksen julkaisemista, vaikka se ei ollut (eikä ehkä koskaan olisi) valmis, vaikka heidän oli pakko julkaista se omalla kustannuksellaan, koska yksikään kaupallinen kustantaja ei halunnut koskea siihen.
Principia Mathematica

Pieni osa ”Principia Mathematican” pitkästä todisteesta, että 1+1 =2
Jonkinlaisen käsityksen ”Principia”-teoksen laajuudesta ja ymmärrettävyydestä saa siitä, että sen lopullisen todisteen, että 1 + 1 = 2, todistaminen vie yli 360 sivua.
Tänä päivänä sitä pidetään yleisesti yhtenä tärkeimmistä ja merkittävimmistä logiikan teoksista sitten Aristoteleen ”Organonin”. Se vaikutti huomattavan onnistuneelta ja sitkeältä kunnianhimoisissa tavoitteissaan, ja se saavutti pian Russellin ja Whiteheadin maailmanmaineen. Itse asiassa vasta Gödelin vuonna 1931 esittämä epätäydellisyysteoreema osoitti lopulta, että ”Principia” ei voinut olla sekä johdonmukainen että täydellinen.
Russellille myönnettiin ansioristi vuonna 1949 ja Nobelin kirjallisuuspalkinto seuraavana vuonna. Hänen maineensa jatkoi kasvuaan myös akateemisten piirien ulkopuolella, ja hänestä tuli myöhemmässä elämässään jonkinlainen kotimainen nimi, tosin pitkälti filosofisen panoksensa sekä poliittisen ja yhteiskunnallisen aktivisminsa ansiosta, jota hän jatkoi pitkän elämänsä loppuun asti. Hän kuoli influenssaan rakkaassa Walesissaan 97-vuotiaana.
| << Takaisin Hardyyn ja Ramanujaniin | Eteenpäin Hilbertiin >> |