Delta-Delta-Ct-menetelmä eli Livak-menetelmä on suositeltavin menetelmä qPCR-tietojen analysoinnissa. Sitä voidaan kuitenkin käyttää vain, jos tietyt kriteerit täyttyvät. tutustu luentomonisteeseen varmistaaksesi, että nämä kriteerit täyttyvät. Jos näin ei ole, yleisempi menetelmä on nimeltään Pfaffl-menetelmä. Lue lisälukumateriaali saadaksesi lisätietoja tästä menetelmästä.
Tässä ovat Livak-menetelmän vaiheet:
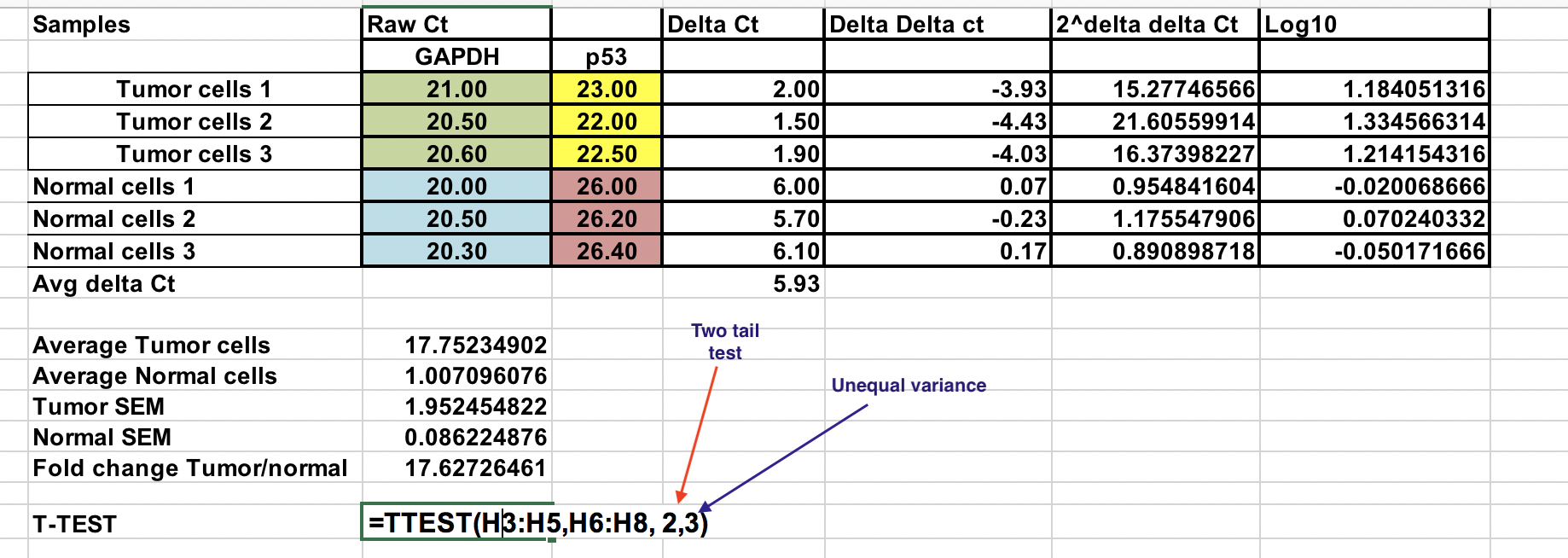
Excel-tiedosto, jossa on kaikki laskelmat, on qPCR-analyysi-kansiossa Blackboardissa.
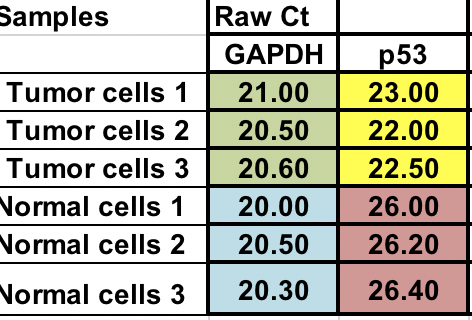
Sinulla on raa’at Ct-arvot (syklien määrä, joka tarvitaan kynnysarvon saavuttamiseen) normaaleille ja kasvainsoluille (3 toistoa kummallekin).
Normalisointi¶
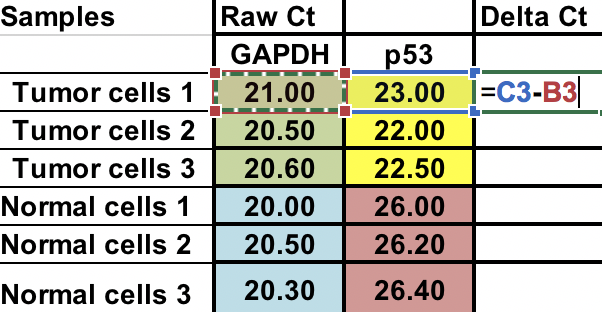
Ensiksi sinun täytyy laskea suhteellinen ero kiinnostuksen kohteena olevan geenin (p53) ja kodinhoitogeenin (GAPDH) välillä.
∆Ct = Ct (kiinnostuksen kohteena oleva geeni) – Ct (houseekeeping-geeni)
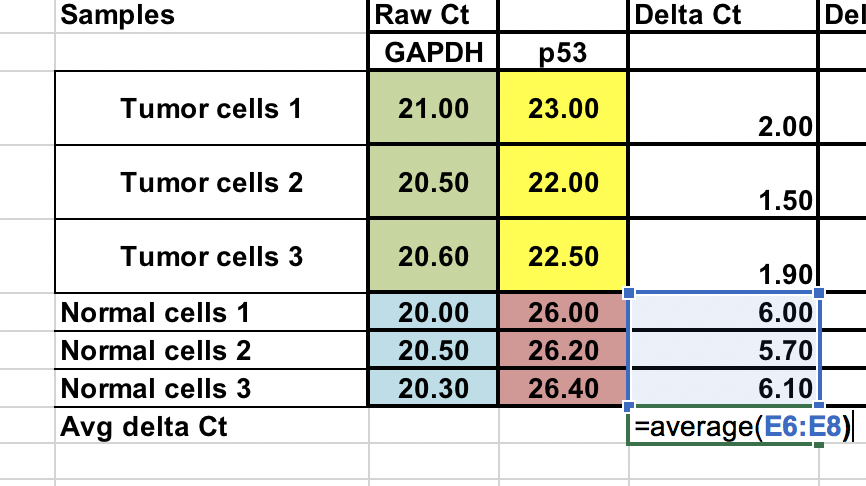
Kontrollinäytteiden (normaalit solut)¶
Vertaamme kasvaintamme (hoitoa) kontrolliin (normaalit solut), meidän on ensin keskiarvoistettava kolmen kontrollinäytteen (normaali) ∆Ct.
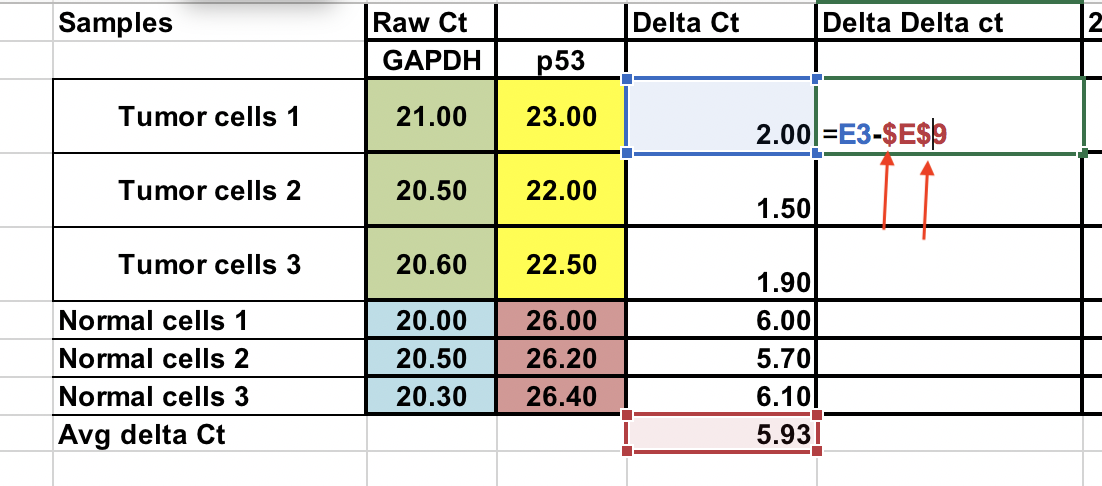
Lasketaan ∆∆Ct suhteessa ∆Ct:n keskiarvoon normaalien soluja¶
∆∆Ct = ∆Ct (kasvainnäyte) – ∆Ct (normaali keskiarvo)
Voit tehdä tämän myös normaaleista näytteistä. Käytä $-merkkejä sarakkeen numeron ja raakakirjaimen (nuolet) edessä solun kiinnittämiseen.
Geeniekspression kertaantuminen jokaiselle näytteelle¶
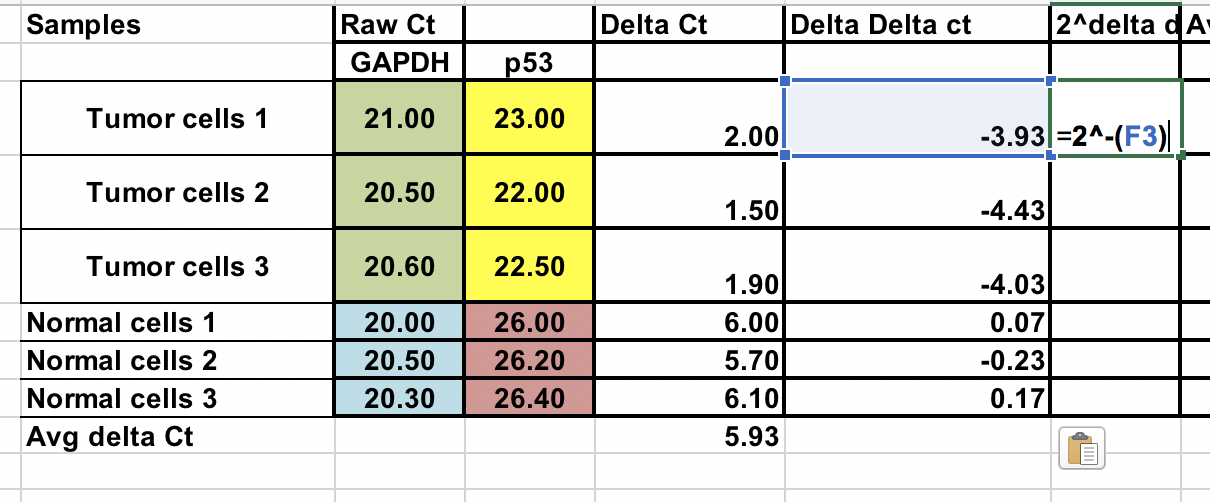
Varmista, että nostat negatiivisen ∆∆Ct:n potenssiin kaksi.
Kertainen geeniekspressio = 2^-(∆∆Ct)
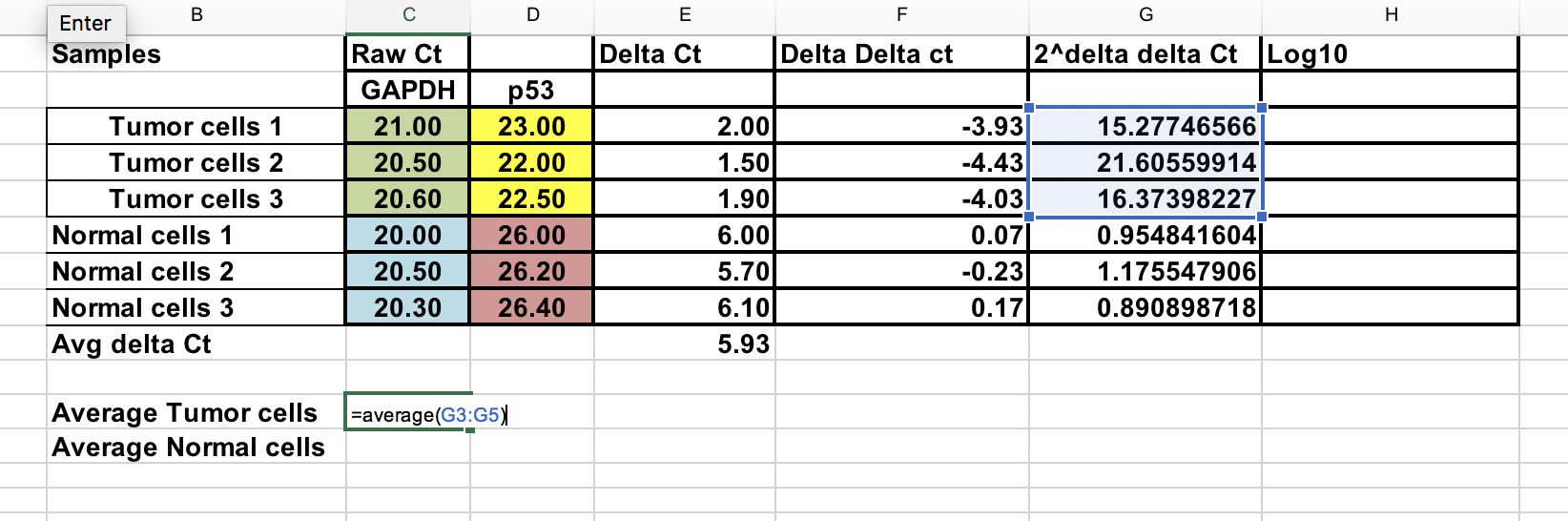
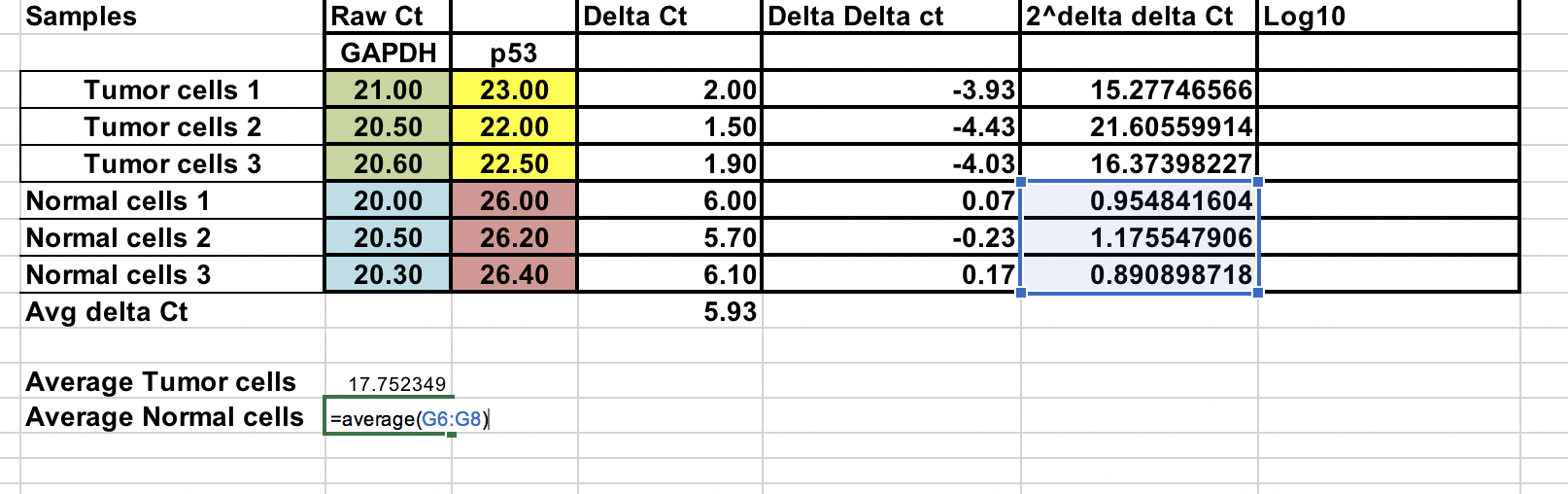
Keskimääräinen kertaistunut muutos¶
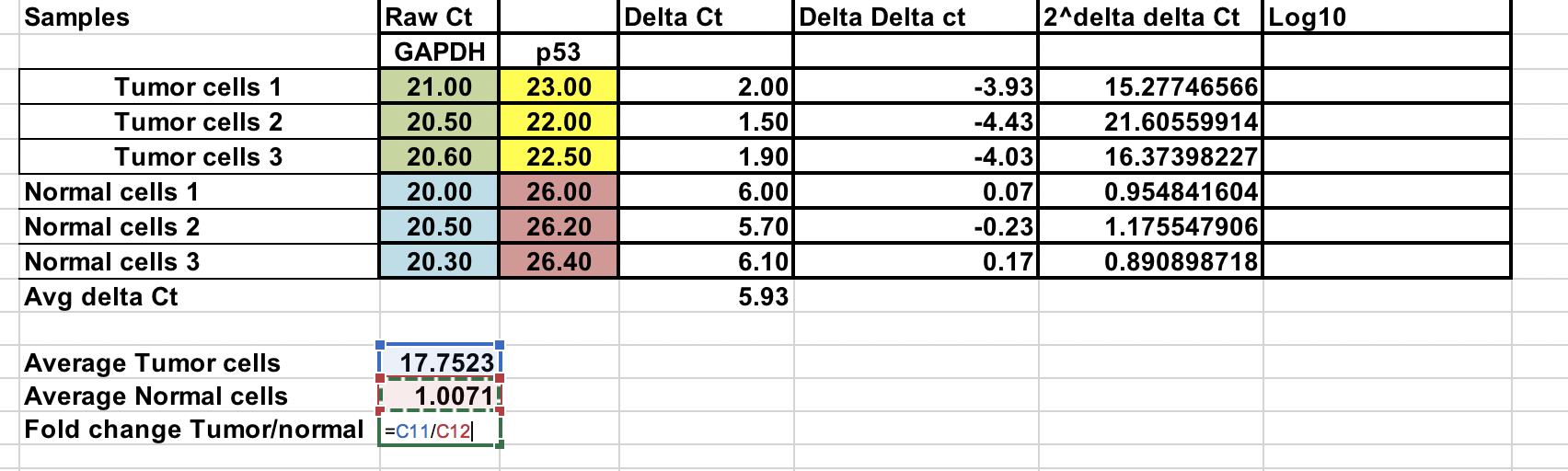
Voit laskea keskimääräisen kertaistuneen muutoksen sekä kasvaimen että normaalin näytteen osalta. Näiden kahden välinen suhde on kasvaimen ja normaalinäytteiden välinen taitosmuutos.
Log-muunnos¶
Parametristen tilastollisten testien, kuten T-testin, suorittamiseksi lopullisten geeniekspressiomenetystuloksien muuntaminen log-arvoiksi (mikä tahansa log-alkio) on suositeltavaa. Tämä tekisi datan jakaumasta symmetrisen.
Tässä olemme muuttaneet 2^-(∆∆Ct) log 10:ksi.
T-testi¶
On oltava varovainen käytettäessä parametrisia testejä, jos data ei ole normaalisti jakaantunutta, se johtaisi virheellisiin päätelmiin.
Valitaan normaalien ja kasvainnäytteiden 2^-(∆∆Ct)-arvojen log 10 -arvot ilmoitetulla tavalla. Käytetään kahden hännän testiä (numero 2) ja oletetaan epätasainen varianssi (3).
Tuloksena saatu P-arvo on pienempi kuin 0,05, joten hylkäämme nollahypoteesin ja kahden otoksen keskiarvot eroavat toisistaan merkitsevästi 0,05 tasolla.