Chemguide: Support for CIE A level Chemistry
Learning outcome 11.2(f)
This statement is about partition coefficents.
Before you go on, you should find and read the statement in your copy of the syllabus.
Jakaantumiskerroin
Jos sinulla on kaksi keskenään sekoittumatonta nestettä, kuten eetteri ja vesi, ja ravistat niitä erotussuppilossa, ne muodostavat ilmeisesti kaksi kerrosta. Eetteri on vähemmän tiheä kuin vesi, ja muodostaa siten ylimmän kerroksen.
Ja nyt oletetaan, että ravistetaan eetterin ja veden seosta, joka sisältää ainetta, joka liukenee molempiin. Oletetaan, että aine X on liukoisempi eetteriin kuin veteen.
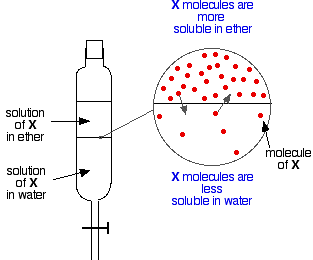
Hiukkaset X:stä ylittävät kahden nestekerroksen välisen rajan, ja pian syntyy dynaaminen tasapaino. Jokaista ylimpään kerrokseen siirtyvää hiukkasta kohden yksi hiukkanen siirtyy takaisin alempaan kerrokseen.
Tälle voisi kirjoittaa yhtälön:
. . ja kuten mikä tahansa muu tasapaino, voit löytää tasapainovakion:
Tätä tasapainovakiota kutsutaan jakaantumiskertoimeksi, ja sille annetaan usein symboli Kpc.
Kuten muutkin tasapainovakiot, jakaantumiskertoimet ovat vakioita vakiolämpötilassa, mutta niillä on myös joitakin muita rajoituksia. Ne toimivat oikein vain melko laimeille liuoksille, ja liuenneen aineen on oltava samassa kemiallisessa muodossa molemmissa liuottimissa. Se ei saa reagoida, ionisoitua tai assosioitua (liittyä esimerkiksi dimeereiksi).
Jakaantumiskertoimen laskeminen
Huomautus yksiköistä
Huomaa, että jakaantumiskerroin on yksinkertainen kahden konsentraation suhde. Sillä ei ole väliä, mitä konsentraatioyksiköitä käytät – kunhan käytät samoja yksiköitä ylhäällä ja alhaalla.
Voisit käyttää mol dm-3, mutta useammin käytetään g cm-3 – grammaa kuutiosenttimetriä kohti.
Teknisesti hakasulkeita voidaan käyttää vain konsentraatioille, jotka ilmoitetaan mol dm-3:ssa, mutta Application Support Booklet -kirjasessa ja CIE:n pisteytysjärjestelmissä sitä käytetään myös muiden yksiköiden yhteydessä.
En ole valmis tekemään niin, joten käytän mieluummin termiä ”X:n konsentraatio” kuin missä käytetään epätyypillisiä konsentraatioyksiköitä.
Jakaantumiskertoimen laskeminen
Kun liuosta, jossa oli 1,00 g X:ää 100 cm3:ssa vettä, ravistettiin 10 cm3:n eetterin kanssa, eetterikerrokseen siirtyi 0,80 g X:ää. Laske X:n jakautumiskerroin eetterin ja veden välillä.
Jos sinua pyydetään laskemaan jakautumiskerroin kahden liuottimen välillä, ensin mainitun liuottimen konsentraatio menee Kpc-lausekkeen päälle. Eli tässä tapauksessa:
Sinulla on tarpeeksi tietoa laskea molempien pitoisuudet g cm-3:na.
X:n pitoisuus eetterissä = 0,80/10 g cm-3
Jos 0,80 g siirtyisi eetteriin, 1,00 – 0,80 g = 0.Veteen jäi 20 g.
X:n pitoisuus vedessä = 0,20/100 g cm-3
Siten:
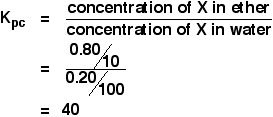
Voit tietenkin laskea pitoisuudet eetterissä ja vedessä todellisina lukuina ennen kuin laitat ne lausekkeeseen. Tee se niin kuin sinusta tuntuu mukavimmalta.
Tämmöisillä jakaantumiskertoimilla ei ole yksiköitä – yksiköt mitätöityvät, koska ne ovat samat ylhäällä ja alhaalla.
Jakaantumiskertoimia sisältäviä laskutoimituksia
CIE:n opetussuunnitelmassa sanotaan nimenomaan, että sinun pitäisi osata laskea jakaantumiskerroin (eli se, mitä me juuri teimme). Siinä ei sanota yhtään mitään niiden käyttämisestä muiden asioiden laskemiseen. Näitä ylimääräisiä laskutoimituksia käsitellään Application Support Booklet -kirjassa, ja niitä on kysytty kaksi kertaa kokeissa kesäkuuhun 2013 asti (molemmat vuonna 2009).
Kurssikirja ei sisällä niitä (aivan oikein!), koska opetussuunnitelmassa ei mainita niitä, ja CIE:n tutkinnon vastaanottajat ovat hyväksyneet tämän kirjan ”täydelliseksi ja täsmälliseksi kattavuudeksi” opetussuunnitelmasta. Tarkoittaako tämä siis sitä, että CIE ei enää kysy kysymyksiä tulevaisuudessa? Älä luota siihen!
Perusesimerkki
Käytämme samaa tapausta kuin aiemmin – samat liuottimet, sama X ja sama jakaantumiskerroin, jonka olemme juuri laskeneet.
Tällä kertaa laskemme, kuinka paljon olisi uuttunut eetterikerrokseen, jos olisimme ravistaneet alkuperäistä liuosta, jossa oli 1,00 g X:ää 100 cm3:ssa vettä, vain 5 cm3:lla eetteriä.
Yritämme laskea uuttuneen X:n massan. Kutsutaan sitä nimellä m.
Keksitään nyt lauseke X:n liuoksen konsentraatiolle eetterissä.
X:n konsentraatio eetterissä = m/5 g cm-3
Entä vesi? Veteen jää (1,00 – m) g X:ää. Eli:
X:n pitoisuus vedessä = (1,00 – m)/100 g cm-3
Nyt voit laittaa kaiken tämän jakautumiskertoimen lausekkeeseen. Muista, että olemme jo laskeneet X:n jakautumiskertoimeksi eetterin ja veden välillä 40.
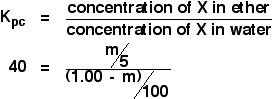
Tällöin edessäsi on vain yksinkertainen, mutta hiukan työläs pätkä algebraa:
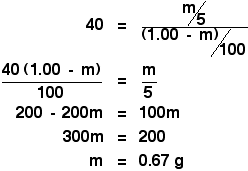
Mitä työläs!
Alkuperäisessä laskelmassa jakaantumiskertoimen löytämiseksi sinulle kerrottiin, että jos ravistat alkuperäistä liuosta, jossa oli 1,00 g X:ää 100 cm3:ssa vettä, 10 cm3:lla eetteriä, saat uutettua 0,80 g X:ää.
Ravistamalla sitä 5 cm3:lla eetteriä olemme juuri laskeneet, että saisit uuttamalla uutetuksi 0,67 g X:ää.
Tällöin 100 cm3:aan vettä jäisi 0,33 g X:ää. Oletetaan, että olisit varovasti säilyttänyt tämän liuoksen ja sitten ravistanut sitä toisella tuoreella 5 cm3 eetterillä.
Minkä verran X:ää saisit yhteensä uutettua käyttämällä eetteriä kahtena erillisenä 5 cm3:n eränä sen sijaan, että olisit käyttänyt 10 cm3:n erää kerralla?
Kutsutaan toisella eetterierällä uutetun X:n massaa nimellä n – jotta emme menisi sekaisin.
Keksitään lauseke X:n eetteriliuoksen konsentraatiolle.
X:n konsentraatio eetterissä = n/5 g cm-3
Entä vesi? Veteen jää (0,33 – n) g X:ää toisen uuton jälkeen. Eli:
X:n pitoisuus vedessä = (0,33 – n)/100 g cm-3
Nyt voit laittaa kaiken tämän X:n jakautumiskertoimen lausekkeeseen eetterin ja veden välillä kuten aiemmin.
Tämä tarkoittaa, että jos yhdistäisit kaksi 5 cm3 :n erää eetteriä, olisit uuttanut yhteensä 0,67 + 0,22 g X:ää, eli 0.89 g.
Sinulle kerrottiin alun perin, että jos olisit tehnyt tämän vain kerran käyttäen eetteriä yhtenä 10 cm3:n eränä, olisit uuttanut vain 0,80 g.
Tehokkaampaan uuttoon pääset jakamalla liuottimesi pienempiin tilavuuksiin, kuten edellä on esitetty.
Tällaista tekniikkaa käytetään joidenkin orgaanisten yhdisteiden valmistuksessa. Uutat sen mitä yrität valmistaa jostain sotkuisesta liuoksesta veteen niin, että se päätyy orgaaniseen liuottimeen. Sen jälkeen poistat liuottimen varovaisella tislauksella.
CIE:ssä kysyttiin samankaltainen kysymys kesäkuun 2009 paperissa 4 Q8. Sinun piti laskea arvo jakautumiskertoimelle ja käyttää sitä sitten kaksivaiheisessa uutossa täsmälleen kuten edellä. Laskelmasta sai 4 pistettä. Tämä voi olla työlästä ja (jakokertoimen laskemista lukuun ottamatta) ei kuulu opetussuunnitelmaan, mutta teillä ei ole varaa olla osaamatta sitä.
