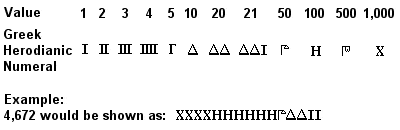
Muinaiskreikkalaiset herodiaaniset numerot
Kreikkalaisen imperiumin alkaessa levittäytyä vaikutusvaltakuntansa piiriin myös Vähä-Aasiaan, Mesopotamiaan ja sen ulkopuolelle, kreikkalaiset olivat tarpeeksi fiksuja omaksumaan ja mukauttamaan hyödyllisiä elementtejä valloittamistaan yhteiskunnista. Tämä päti yhtä lailla heidän matematiikkaansa kuin mihin tahansa muuhunkin, ja he omaksuivat matematiikan elementtejä sekä babylonialaisilta että egyptiläisiltä. Pian he alkoivat kuitenkin antaa merkittäviä omia panoksiaan, ja nyt voimme ensimmäistä kertaa tunnustaa yksittäisten henkilöiden panoksen. Hellenistiseen aikaan mennessä kreikkalaiset olivat johtaneet yhtä kaikkien aikojen dramaattisimmista ja tärkeimmistä vallankumouksista matemaattisessa ajattelussa.
Attilaiset tai herodiaaniset numerot
Vanha kreikkalainen numerojärjestelmä, joka tunnetaan attilaisina tai herodiaanisina numeroina, oli täysin kehittynyt noin 450 eaa. ja säännöllisessä käytössä mahdollisesti jo 7. vuosisadalla eaa. Se oli perusta 10:n järjestelmä, joka muistutti aiempaa egyptiläistä järjestelmää (ja vielä enemmän myöhempää roomalaista järjestelmää), ja sen symbolit 1, 5, 10, 50, 100, 500 ja 1 000 toistettiin niin monta kertaa kuin halutun luvun esittämiseksi tarvittiin. Yhteenlasku tehtiin laskemalla yhteen erikseen yhteenlaskettavien lukujen symbolit (1, 10, 100 jne.), ja kertolasku oli työläs prosessi, joka perustui peräkkäisiin kaksinkertaistuksiin (jako perustui tämän prosessin käänteislukuun).
Thalesin leikkausteoreema
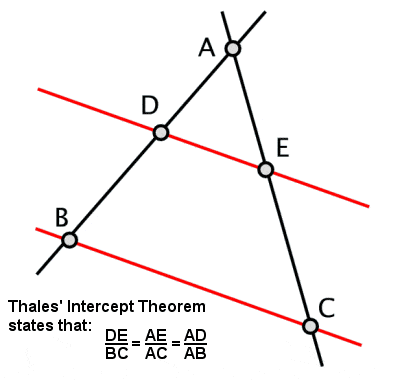
Thalesin leikkausteoreema
Mutta suurin osa kreikkalaisesta matematiikasta perustui geometriaan. Thalesin, yhden antiikin Kreikan seitsemästä tietäjästä, joka eli Vähä-Aasian Joonianmeren rannikolla 6. vuosisadan alkupuoliskolla eaa., katsotaan yleensä olleen ensimmäinen, joka loi suuntaviivat geometrian abstraktille kehitykselle, vaikka se, mitä tiedämme hänen työstään (esimerkiksi samankaltaisista ja suorakulmaisista kolmioista), vaikuttaa nykyään varsin alkeelliselta.
Thales loi niin sanotun Thalesin lauseen, jonka mukaan jos kolmio piirretään ympyrän sisälle siten, että sen pitkä sivu on ympyrän halkaisija, vastakkainen kulma on aina suorakulmainen (sekä joitakin muita tästä johdettuja asiaan liittyviä ominaisuuksia). Hänelle on myös uskottu toinen teoreema, joka tunnetaan myös nimellä Thalesin teoreema tai leikkausteoreema ja joka koskee niiden suorasegmenttien suhdetta, jotka syntyvät, jos kaksi toisiaan leikkaavaa suoraa leikataan samansuuntaisella parilla (ja laajemmassa merkityksessä samankaltaisten kolmioiden sivujen suhdetta).
Jossain määrin 6. vuosisadalla eaa. eläneen samoslaisen matemaatikon Pythagoraan legenda on kuitenkin muodostunut synonyymiksi kreikkalaisen matematiikan synnyn kanssa. Hänen uskotaankin keksineen sekä sanat ”filosofia” (”viisauden rakkaus”) että ”matematiikka” (”se, mitä opitaan”). Pythagoras oli ehkä ensimmäinen, joka tajusi, että voidaan rakentaa täydellinen matematiikkajärjestelmä, jossa geometriset elementit vastaavat numeroita. Pythagoraan lause (tai Pythagoraan lause) on yksi tunnetuimmista matemaattisista lauseista. Hän on kuitenkin edelleen kiistelty hahmo, kuten tulemme näkemään, eikä kreikkalainen matematiikka suinkaan rajoittunut vain yhteen mieheen.
Kolme geometrista ongelmaa
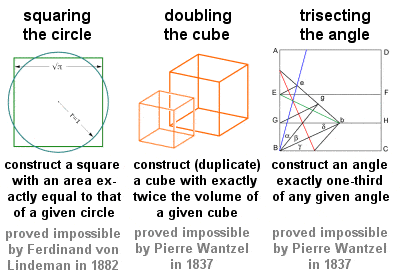
Kolme klassista ongelmaa
Kreikkalaisen geometrian alkuaikoihin juontaa juurensa erityisesti kolme geometrista ongelmaa, joita usein kutsutaan nimellä Kolme klassista ongelmaa ja jotka kaikki on ratkaistava puhtaasti geometrisin keinoin käyttäen vain viivainta ja kompassia: ”ympyrän neliöiminen (tai kvadratuuri)”, ”kuution kaksinkertaistaminen (tai monistaminen)” ja ”kulman kolmioiminen”. Nämä tinkimättömät ongelmat vaikuttivat syvästi tulevaan geometriaan ja johtivat moniin hedelmällisiin keksintöihin, vaikka niiden varsinaisia ratkaisuja (tai, kuten kävi ilmi, todisteita niiden mahdottomuudesta) jouduttiin odottamaan 1800-luvulle asti.
Hippokrates Khioslainen (ei pidä sekoittaa suureen kreikkalaiseen lääkäriin Hippokrates Kosin. Yksityiskohtainen elämäkerta täällä.) oli yksi tällainen kreikkalainen matemaatikko, joka sovelsi itseään näihin ongelmiin 5. vuosisadalla eKr. (hänen panoksensa ”ympyrän neliön neliöimisen” ongelmaan tunnetaan nimellä Hippokrateen Lune). Hänen vaikutusvaltainen kirjansa ”Elementit”, joka on peräisin noin vuodelta 440 eaa., oli ensimmäinen kokoelma geometrian alkeita, ja hänen teoksensa oli tärkeä lähde Eukleideen myöhemmille töille.
Zenon paradoksi Akhilleuksesta ja kilpikonnasta
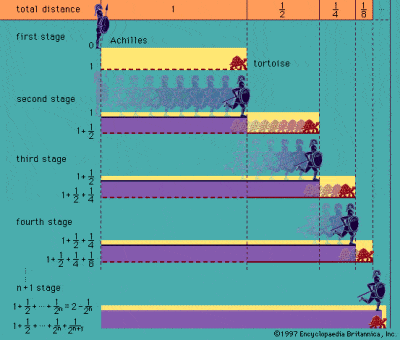
Zenon paradoksi Akhilleuksesta ja kilpikonnasta
Kreikkalaiset olivat niitä, jotka ensimmäisenä pohtivat ajatusta äärettömyydestä, kuten esimerkiksi tunnetuissa paradokseissa kuvatut paradoksit kuvaavat filosofi Zenon Elealainen 5. vuosisadalla eaa. väitetyn. Tunnetuin hänen paradokseistaan on Akhilleuksen ja kilpikonnan paradoksi, jossa kuvataan Akhilleuksen ja kilpikonnan välistä teoreettista kilpajuoksua. Akilles antaa paljon hitaammalle kilpikonnalle etumatkaa, mutta kun Akilles saavuttaa kilpikonnan lähtöpisteen, kilpikonna on jo siirtynyt eteenpäin. Kun Akilles saavuttaa tämän pisteen, kilpikonna on taas edennyt eteenpäin jne. jne., joten periaatteessa nopea Akilles ei voi koskaan saavuttaa hidasta kilpikonnaa.
Tällaiset paradoksit kuten tämä ja Zenonin niin sanottu dikotomiaparadoksi perustuvat avaruuden ja ajan äärettömään jaettavuuteen, ja ne perustuvat ajatukseen, että puolikas plus neljäsosa plus kahdeksasosa plus kahdeksasosa plus kuudestoistaosa jne. jne. jne. äärettömään ei koskaan ole aivan yhtä suuri kuin kokonaisuus. Paradoksi juontaa kuitenkin juurensa väärästä olettamuksesta, jonka mukaan ääretön määrä erillisiä viivoja on mahdotonta saada valmiiksi äärettömässä ajassa, vaikkakin harhaluuloa on äärimmäisen vaikea todistaa lopullisesti. Antiikin kreikkalainen Aristoteles oli ensimmäinen monista, joka yritti kumota paradoksin, varsinkin kun hän uskoi vakaasti, että ääretön voi aina olla vain potentiaalinen eikä todellinen.
Demokritos, joka on tunnetuin kaukokatseisista ajatuksistaan siitä, että kaikki aine koostuu pienistä atomeista, oli myös matematiikan ja geometrian edelläkävijä 5.-4. vuosisadalla eaa., ja hän tuotti teoksia, joiden otsikot olivat ”Luvuista”, ”Geometriasta”, ”Tangentiaalisuudesta”, ”Kartoituksesta” ja ”Irrationaalisuudesta”, vaikkakaan nämä teokset eivät ole säilyneet. Tiedämme, että hän oli ensimmäisten joukossa havaitsemassa, että kartion (tai pyramidin) tilavuus on kolmasosa sylinterin (tai prisman) tilavuudesta, jolla on sama pohja ja korkeus, ja hän on ehkä ensimmäinen, joka on vakavasti pohtinut esineiden jakamista äärettömään määrään poikkileikkauksia.
On kuitenkin varmasti totta, että erityisesti Pythagoras vaikutti suuresti hänen jälkeensä tulleisiin, kuten Platoniin, joka perusti kuuluisan akatemiansa Ateenaan vuonna 387 eaa., ja hänen suojattinsa Aristoteles, jonka logiikkaa koskevaa teosta pidettiin lopullisena yli kahden tuhannen vuoden ajan. Matemaatikko Platon tunnetaan parhaiten kuvauksestaan viidestä platonisesta kiinteästä kappaleesta, mutta hänen työnsä arvoa matematiikan opettajana ja popularisoijana ei voi liioitella.
Platonin oppilaan Eudoksos Niduksen Eudoksoksen katsotaan yleensä toteuttaneen ensimmäisen kerran ”uupumuksen menetelmän” (jonka Arkhimedes kehitti sittemmin), varhaisen integrointimenetelmän peräkkäisten approksimaatioiden avulla, ja hän käytti sitä laskiessaan pyramidin ja kartion tilavuutta. Hän kehitti myös yleisen suhteellisuusteorian, jota voitiin soveltaa sekä yhteensopimattomiin (irrationaalisiin) suureisiin, joita ei voida ilmaista kahden kokonaisluvun suhteena, että yhteensopimattomiin (rationaalisiin) suureisiin, ja laajensi näin Pythagoraan epätäydellisiä ajatuksia.
Kreikkalaisten ehkä tärkein yksittäinen panos oli kuitenkin – ja Pythagoras, Platon ja Aristoteles olivat kaikki vaikutusvaltaisia tässä suhteessa – ajatus todistamisesta ja deduktiivinen menetelmä, jossa loogisten vaiheiden avulla todistetaan tai kumotaan teoreemoja alun perin oletetuista aksioomista. Vanhemmissa kulttuureissa, kuten egyptiläisissä ja babylonialaisissa, luotettiin induktiiviseen päättelyyn eli toistuvien havaintojen käyttämiseen nyrkkisääntöjen laatimiseksi. Juuri tämä todistamisen käsite antaa matematiikalle sen voiman ja varmistaa, että todistetut teoriat ovat yhtä totta nykyään kuin kaksi tuhatta vuotta sitten, ja se loi perustan Eukleideen ja hänen jälkeensä tulleiden systemaattiselle lähestymistavalle matematiikkaan.
| << Takaisin egyptiläiseen matematiikkaan | Eteenpäin Pythagoraan >> |