Kun esine liikkuu nesteen läpi tai neste liikkuu esineen ohi,esineen lähellä olevan nesteen molekyylit häiriintyvät ja liikkuvat esineen ympärillä.Aerodynaamiset voimat syntyvät nesteen ja esineen välille. Näiden voimien suuruus riippuu esineen muodosta, esineen nopeudesta, esineen ohi kulkevan nesteen massasta ja kahdesta muusta tärkeästä nesteen ominaisuudesta: nesteen viskositeetista eli tahmeudesta ja nesteen kokoonpuristuvuudesta eli jousittavuudesta. Näiden vaikutusten asianmukaiseen mallintamiseen ilmailuinsinöörit käyttävät samankaltaisuusparametreja, jotka ovat näiden vaikutusten suhteita muihin ongelmassa esiintyviin voimiin. Jos kahdella kokeella on samat arvot samankaltaisuusparametreille, voimien suhteellinen merkitys mallinnetaan oikein.
Aerodynaamiset voimat riippuvat monimutkaisella tavalla nesteen viskositeetista. Kun neste liikkuu kohteen ohi, aivan pinnan vieressä olevat molekyylit tarttuvat pintaan. Aivan pinnan yläpuolella olevat molekyylit hidastuvat törmätessään pintaan tarttuvien molekyylien kanssa.Nämä molekyylit puolestaan hidastavat juuri niiden yläpuolella olevaa virtausta. Mitä kauemmaksi pinnasta siirrytään, sitä vähemmän törmäykset vaikuttavat kohteen pintaan. Näin syntyy ohut nestekerros lähelle pintaa, jossa nopeus muuttuu nollasta pinnalla vapaaseen virtausarvoon poispäin pinnasta. Insinöörit kutsuvat tätä kerrosta rajakerrokseksi, koska se tapahtuu nesteen rajalla.
Rajakerroksen sisällä tapahtuvan virtauksen yksityiskohdat ovat hyvin tärkeitä monien aerodynamiikan ongelmien kannalta, kuten siiven sakkaaminen, kappaleen ihokitkan aiheuttama raahautuminen ja suurnopeuslennossa tapahtuva lämmönsiirtyminen.Valitettavasti rajakerrosten fysikaaliset ja matemaattiset yksityiskohdat ylittävät tämän aloittelevalle opiskelijalle suunnatun oppaan soveltamisalan, ja niitä opiskellaan yleensä loppuvaiheessa korkeakoulussa. Esittelemme tällä kertaa vain joitakin rajakerroksen vaikutuksia.
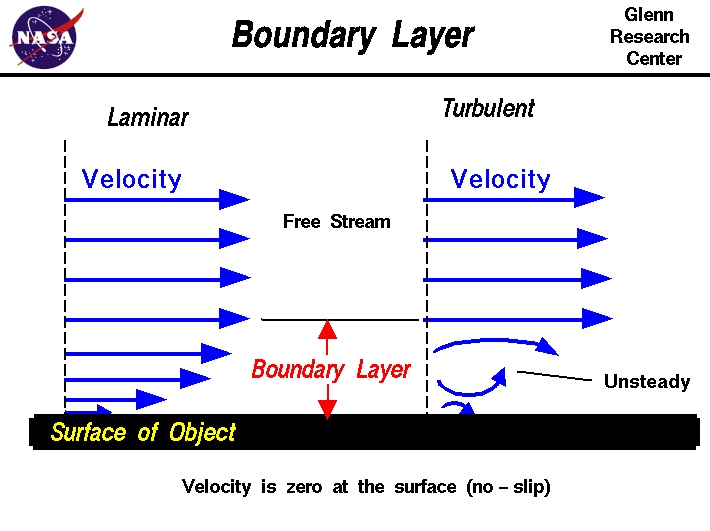
Diassa on esitetty virtaussuuntainen nopeuden vaihtelu vapaasta virtauksesta pintaan. Todellisuudessa vaikutukset ovat kolmiulotteisia. Koska massa säilyy kolmiulotteisesti, nopeuden muutos virtaussuunnassa aiheuttaa nopeuden muutoksen myös muissa suunnissa. Pintaa vastaan kohtisuorassa on pieni nopeuskomponentti, joka siirtää tai liikuttaa virtausta pinnan yläpuolella. Rajakerroksen paksuus voidaan määritellä tämän siirtymän suuruudeksi. Siirtymän paksuus riippuu Reynoldsin luvusta, joka on inertiaalisten (muutosta tai liikettä vastustavien) voimien ja viskoosisten (raskaiden ja liimautuvien) voimien suhde ja joka saadaan yhtälöstä : Reynoldsin luku (Re) on yhtä suuri kuin nopeus (V) kertaa tiheys (r) kertaa ominaispituus (l) jaettuna viskositeettikertoimella (mu).
Re = V * r * l / mu
Rajakerrokset voivat olla joko laminaarisia (kerroksellisia) tai turbulenttisia (epäsäännöllisiä)Reynoldsin luvun arvosta riippuen.Pienemmillä Reynoldsin luvuilla rajakerros on laminaarinenja virtaussuuntainen nopeus muuttuu tasaisesti siirryttäessä poispäin seinämästä, kuten kuvan vasemmalla puolella on esitetty.Suuremmilla Reynoldsin luvuilla rajakerros on turbulenttinen, ja virtaussuuntaiselle nopeudelle on ominaista epästabiili (ajan myötä muuttuva) pyörteinen virtaus rajakerroksen sisällä.Ulkoinen virtaus reagoi rajakerroksen reunaan aivan kuten se reagoisi kappaleen fyysiseen pintaan.Niinpä rajakerros antaa mille tahansa kappaleelle ”tehollisen” muodon, joka yleensä poikkeaa hieman fyysisestä muodosta.Hämmentävämmin rajakerros voi irrota irti tai ”irrottautua” kappaleesta ja luoda tehollisen muodon, joka poikkeaa paljon fyysisestä muodosta. Tämä johtuu siitä, että rajakerroksen virtauksen energia on hyvin pieni (suhteessa vapaaseen virtaukseen) ja sitä ohjaavat helpommin paineen muutokset. Virtauksen irtoaminen on syy siiven sakkaamiseen suurilla kohtauskulmilla.Rajakerroksen vaikutukset nosteeseen sisältyvät nostokertoimeen ja vaikutukset vetovastukseen sisältyvät vetovastuskertoimeen.
HISTORIALLINEN HUOMAUTUS: Rajakerroksen vaikutuksia kuvaavan teorian esitti ensimmäisen kerran Ludwig Prandtl 1900-luvun alussa. Yleiset nesteyhtälöt olivat olleet tiedossa jo vuosia, mutta yhtälöiden ratkaisut eivät kuvailleet oikein havaittuja virtausvaikutuksia (kuten siiven sakkaamista). Prandtl oli ensimmäinen, joka havaitsi, että inertiavoimien ja viskoosivoimien suhteellinen suuruus muuttui hyvin lähellä pintaa olevasta kerroksesta kaukana pinnasta olevaan alueeseen. Hän ehdotti ensimmäisenä vuorovaikutteisesti kytkettyä kaksikerrosratkaisua, joka mallintaa asianmukaisesti monia virtausongelmia.
Tehtäviä: ![]() Opastetut kierrokset
Opastetut kierrokset
-
 Vetovoiman lähteet:
Vetovoiman lähteet: 
-
 Sisäänmeno:
Sisäänmeno: 
Navigointi ..
![]()
![]()
![]()
![]()
![]()
Oppaan aloittelijan aloitussivu