Lohkokaaviot koostuvat yhdestä lohkosta tai lohkojen yhdistelmästä. Niitä käytetään ohjausjärjestelmien esittämiseen kuvallisessa muodossa.
Lohkokaavion peruselementit
Lohkokaavion peruselementtejä ovat lohko, summapiste ja ottopiste. Tarkastellaan seuraavassa kuvassa esitettyä suljetun säätöjärjestelmän lohkokaaviota näiden elementtien tunnistamiseksi.
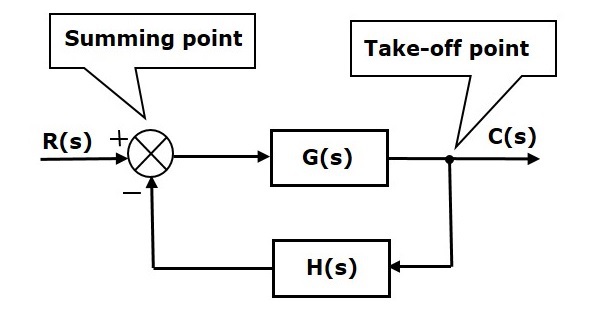
Yllä oleva lohkokaavio koostuu kahdesta lohkosta, joilla on siirtofunktiot G(s) ja H(s). Siinä on myös yksi yhteenlaskupiste ja yksi lähtöpiste. Nuolet osoittavat signaalien kulkusuunnan. Käsitellään nyt näitä elementtejä yksi kerrallaan.
Lohko
Komponentin siirtofunktio esitetään lohkolla. Lohkolla on yksi tulo ja yksi lähtö.
Seuraavassa kuvassa on lohko, jolla on tulo X(s), lähtö Y(s) ja siirtofunktio G(s).

siirtofunktio,$G(s)=\frac{Y(s)}{X(s)}$
$$\oikea nuoli Y(s)=G(s)X(s)$$
Lohkon ulostulo saadaan kertomalla lohkon siirtofunktio sisääntulolla.
Summapiste
Summapiste esitetään ympyrällä, jonka sisällä on risti (X). Siinä on kaksi tai useampi tulo ja yksi lähtö. Se tuottaa tulojen algebrallisen summan. Se suorittaa myös tulojen yhteen- tai vähennyslaskun tai yhteen- ja vähennyslaskun yhdistelmän tulojen napaisuuden perusteella. Tarkastellaan näitä kolmea operaatiota yksitellen.
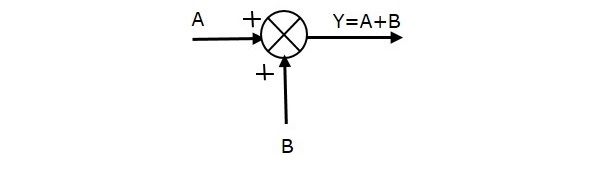
Seuraavassa kuvassa on yhteenlaskupiste, jossa on kaksi tuloa (A, B) ja yksi lähtö (Y). Tässä tuloilla A ja B on positiivinen merkki. Summauspiste tuottaa siis tuloksen, Y, A:n ja B:n summana.
s.o.,Y = A + B.
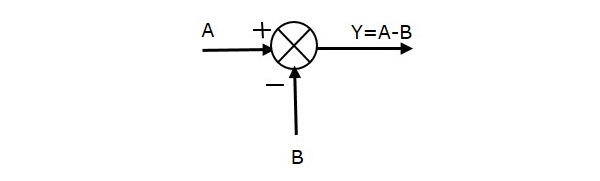
Seuraavassa kuvassa on esitetty summauspiste, jossa on kaksi tuloa (A, B) ja yksi lähtö (Y). Tässä tuloilla A ja B on vastakkaiset merkit, eli A:lla on positiivinen ja B:llä negatiivinen merkki. Summapiste tuottaa siis ulostulon Y A:n ja B:n erotuksena.
Y = A + (-B) = A – B.
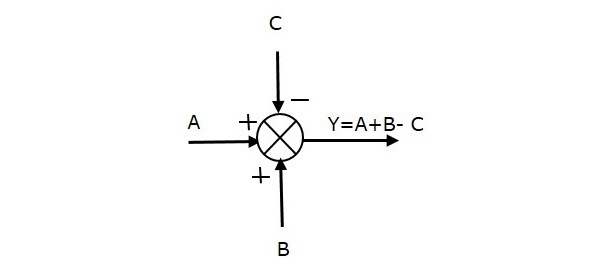
Seuraavassa kuvassa on summapiste, jossa on kolme tuloa (A, B, C) ja yksi ulostulo (Y). Tässä tuloilla A ja B on positiivinen merkki ja C:llä negatiivinen merkki. Summapiste tuottaa siis ulostulon Y seuraavasti
Y = A + B + (-C) = A + B – C.
Vastaanottopiste
Vastaanottopiste on piste, josta sama tulosignaali voidaan johtaa useamman kuin yhden haaran kautta. Se tarkoittaa, että take-off-pisteen avulla voimme soveltaa samaa tuloa yhteen tai useampaan lohkoon, summapisteisiin.
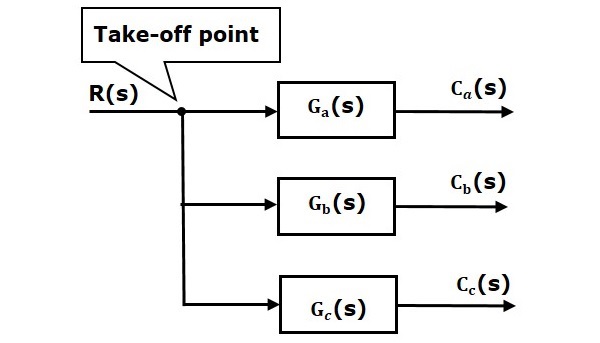
Oheisessa kuvassa take-off-pistettä käytetään saman tulon, R(s), kytkemiseen kahteen muuhun lohkoon.
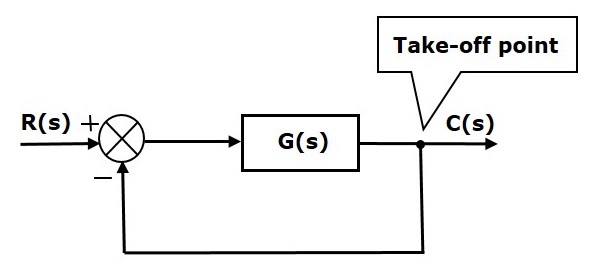
Seuraavassa kuvassa ottopistettä käytetään kytkemään lähtö C(s), yhdeksi tuloksi yhteenlaskupisteeseen.
Sähköjärjestelmien lohkokaavioesitys
Tässä jaksossa esitetään sähköjärjestelmä lohkokaavion avulla. Sähköiset järjestelmät sisältävät pääasiassa kolme peruselementtiä – vastuksen, induktorin ja kondensaattorin.
Harkitaan seuraavassa kuvassa esitettyä RLC-sarjan piiriä. Jossa Vi(t) ja Vo(t) ovat tulo- ja lähtöjännitteet. Olkoon i(t) piirin läpi kulkeva virta. Tämä piiri on aika-alueella.
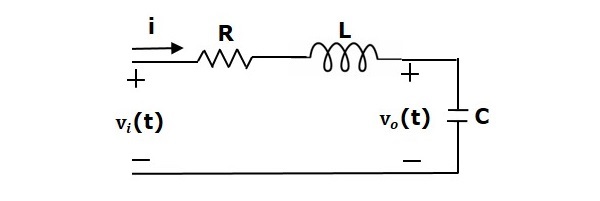
Soveltamalla Laplace-muunnosta tähän piiriin, saadaan piiri s-alueella. Piiri on seuraavan kuvan mukainen.
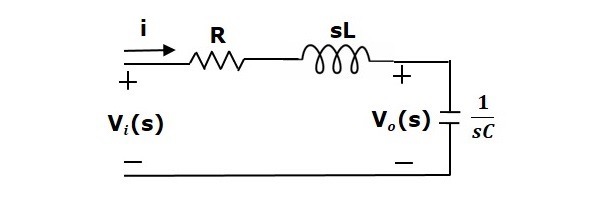
Yllä olevasta piiristä voidaan kirjoittaa
$$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$
$\\ Oikea nuolinäppäin I(s)=\left \{ \frac{1}{R+sL}{R+sL} \oikea \}}\left \{ V_i(s)-V_o(s) \oikea \}$ (Yhtälö 1)
$V_o(s)=\left ( \frac{1}{sC} \oikea )I(s)$ (Yhtälö 2)
Piirretään seuraavaksi lohkokaaviot näille kahdelle yhtälölle erikseen. Ja yhdistetään sitten nämä lohkokaaviot oikein, jotta saadaan RLC-piirin sarjan kokonaislohkokaavio (s-domain).
Yhtälö 1 voidaan toteuttaa lohkolla, jolla on siirtofunktio, $\frac{1}{R+sL}$. Tämän lohkon tulo ja lähtö ovat $\left \{ V_i(s)-V_o(s) \right \}$ ja $I(s)$. Tarvitaan summapiste, jotta saadaan $\left \{ V_i(s)-V_o(s) \right \}$. Yhtälön 1 lohkokaavio on esitetty seuraavassa kuvassa.
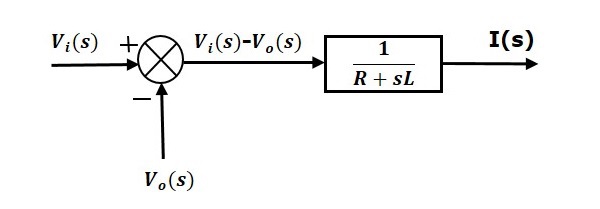
Yhtälö 2 voidaan toteuttaa lohkolla, jolla on siirtofunktio $\frac{1}{sC}$. Tämän lohkon tulo ja lähtö ovat $I(s)$ ja $V_o(s)$. Yhtälön 2 lohkokaavio on esitetty seuraavassa kuvassa.
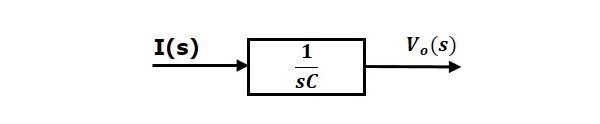
RLC-piirin sarjan (s-domain) kokonaislohkokaavio on esitetty seuraavassa kuvassa.
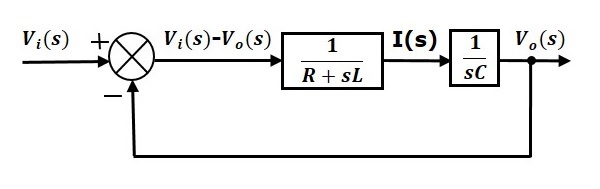
Samoin voit piirtää minkä tahansa sähköisen piirin tai järjestelmän lohkokaavion noudattamalla tätä yksinkertaista menettelyä.
-
Muunnetaan aikatason sähköpiiri s-domainin sähköpiiriksi soveltamalla Laplace-muunnosta.
-
Kirjoita ylös yhtälöt kaikkien sarjahaarojen elementtien läpi kulkevalle virralle ja kaikkien shunttihaarojen yli kulkevalle jännitteelle.
-
Piirrä lohkokaaviot kaikille edellä mainituille yhtälöille erikseen.
-
Yhdistetään kaikki nämä lohkokaaviot oikein, jotta saadaan sähköpiirin kokonaislohkokaavio (s-domain).