16.3 Sekastrategiat
Oppimistavoite
- Mitkä pelit vaativat tai sallivat satunnaistamisen osana ratkaisua?
Katsotaanpa vielä kerran pennien yhteensovittamispeliä, jota havainnollistaa kuva 16.13 ”Matching pennies again”.
Kuvio 16.13 Matching pennies again
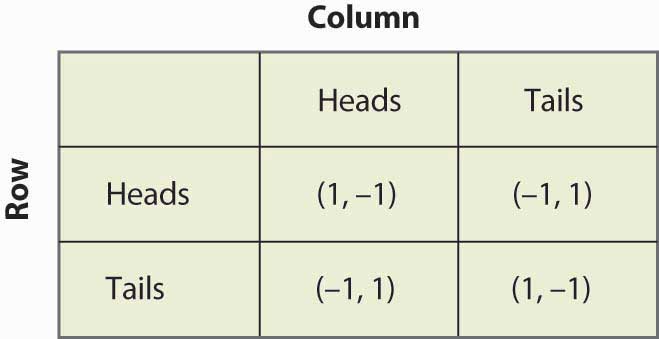
Asetetaan, että Rivi uskoo Sarakkeen pelaavan Kruuna todennäköisyydellä p. Silloin jos Rivi pelaa Kruuna-peliä, Rivi saa arvon 1 todennäköisyydellä p ja arvon -1 todennäköisyydellä (1 – p) odotusarvolla 2p – 1. Vastaavasti, jos Rivi pelaa Kruuna, Rivi saa -1 todennäköisyydellä p (kun Sarake pelaa Kruuna) ja 1 todennäköisyydellä (1 – p), jolloin odotusarvo on 1 – 2p. Tämä on esitetty tiivistetysti kuvassa 16.14 ”Mixed strategy in matching pennies”.
Jos 2p – 1 > 1 – 2p, niin Rivin on keskimäärin parempi pelata Kruuna kuin Klaava. Vastaavasti, jos 2p – 1 < 1 – 2p, niin Rivi on parempi pelaamaan klaavaa kuin kruunaa. Jos taas 2p – 1 = 1 – 2p, Row saa saman voiton riippumatta siitä, mitä Row tekee. Tällöin Row voisi pelata kruunua, pelata klaavaa tai heittää kolikkoa ja satunnaistaa Row:n pelin.
Sekastrategian Nash-tasapainoNash-tasapaino, jossa vähintään yksi pelaaja pelaa satunnaistettua strategiaa eikä yksikään pelaaja pysty kasvattamaan odotettavissa olevaa voittoaan pelaamalla vaihtoehtoista strategiaa. liittyy siihen, että vähintään yksi pelaaja pelaa satunnaistettua strategiaa eikä yksikään pelaaja pysty kasvattamaan odotettavissa olevaa voittoaan pelaamalla vaihtoehtoista strategiaa. Nash-tasapainoa, jossa yksikään pelaaja ei satunnaista, kutsutaan puhtaan strategian Nash-tasapainoksiNash-tasapaino, jossa yksikään pelaaja ei satunnaista..
Kuvio 16.14 Sekastrategia pennien yhteensovittamisessa
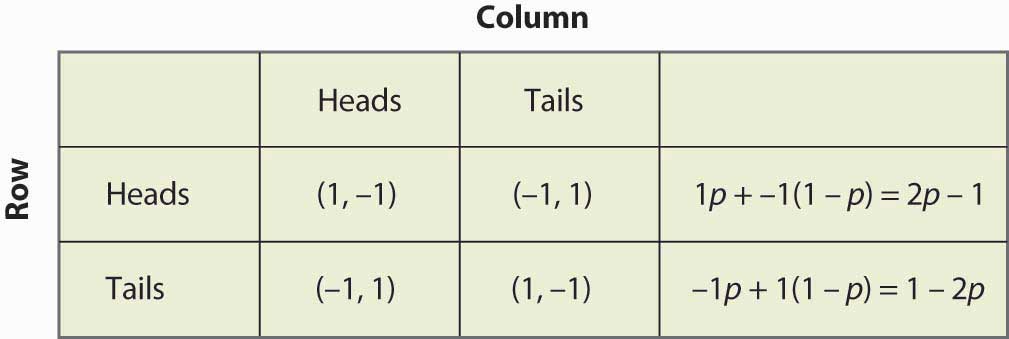
Huomaa, että satunnaistaminen edellyttää odotettavissa olevien hyötyjen tasa-arvoa. Jos pelaajan oletetaan satunnaistavan strategian A tai strategian B, molempien strategioiden on tuotettava sama odotettu voitto. Muuten pelaaja suosisi jompaakumpaa eikä pelaisi toista.
Sekastrategian laskemiseen liittyy yksi elementti, joka vaikuttaa usein hämmentävältä. Oletetaan, että Row aikoo satunnaistaa. Silloin Row’n voittojen on oltava samat kaikilla strategioilla, joita Row pelaa positiivisella todennäköisyydellä. Mutta tuo Rown voitonmaksujen yhtäläisyys ei määritä todennäköisyyksiä, joilla Row pelaa eri rivejä. Sen sijaan rivin voittojen yhtäläisyys määrittää todennäköisyydet, joilla sarake pelaa eri sarakkeita. Syy tähän on se, että sarakkeen todennäköisyydet määräävät rivin odotetut voitot; jos rivi aikoo satunnaistaa, sarakkeen todennäköisyyksien on oltava sellaisia, että rivi on halukas satunnaistamaan.
Laskimme siis esimerkiksi rivin voiton, joka saadaan pelaamalla kruuna, joka on 2p – 1, missä p on todennäköisyys sille, että sarake pelaa kruuna. Vastaavasti Rivin voitto siitä, että se pelasi klaavaa, oli 1 – 2p. Row on halukas satunnaistamaan, jos nämä ovat yhtä suuret, mikä ratkaisee p = ½.
Kokeillaan nyt hieman haastavampaa esimerkkiä ja käydään uudelleen läpi sukupuolten välinen taistelu. Kuvio 16.15 ”Mixed strategy in battle of the sexes” havainnollistaa jälleen kerran voittoja.
Kuvio 16.15 Mixed strategy in battle of the sexes
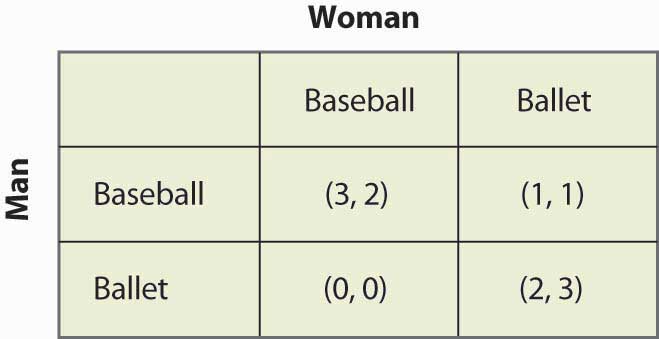
Tässä pelissä on kaksi puhtaan strategian Nash-tasapainoa: (Baseball, Baseball) ja (Ballet, Ballet). Onko olemassa sekastrategiaa? Sekastrategian laskemiseksi annetaan naisen mennä pesäpallopeliin todennäköisyydellä p ja miehen mennä pesäpallopeliin todennäköisyydellä q. Kuvassa 16.16 ”Täydellinen sekastrategian laskenta” on laskettu kunkin pelaajan sekastrategiapalkkiot.
Kuvio 16. Sekastrategian laskenta.16 Sekastrategian täydellinen laskenta
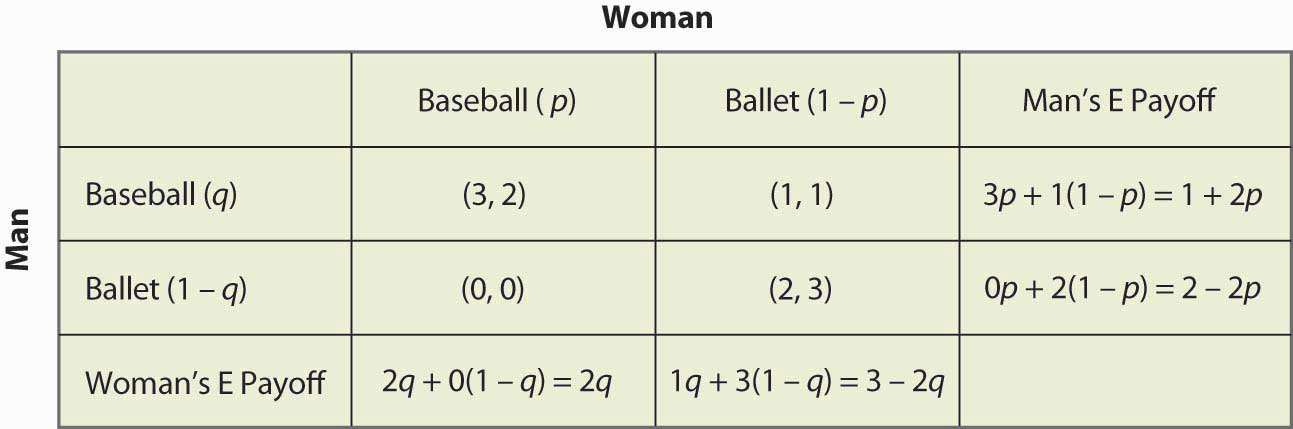
Jos esimerkiksi mies (rivipelaaja) menee pesäpallopeliin, hän saa 3, kun nainen menee pesäpallopeliin (todennäköisyys p), ja muutoin saa 1, jolloin odotettu voitto on 3p + 1(1 – p) = 1 + 2p. Muut laskelmat ovat samankaltaisia, mutta sinun kannattaa ehdottomasti käydä logiikka läpi ja tarkistaa jokainen laskelma.
Sukupuolten taistelu -pelissä sekastrategia edellyttää molempien osapuolten satunnaistamista (koska jommankumman osapuolen puhdas strategia estää toisen osapuolen satunnaistamisen). Miehen välinpitämättömyys pesäpallo- ja pallopeliin menemisen välillä vaatii 1 + 2p = 2 – 2p, jolloin saadaan p = ¼. Toisin sanoen mies on valmis satunnaistamaan, kumpaan tapahtumaan hän osallistuu, jos nainen on menossa balettiin ¾ ajasta ja muuten pesäpallopeliin. Tämä tekee miehestä välinpitämättömän näiden kahden tapahtuman välillä, koska hän haluaa olla mieluummin Naisen kanssa, mutta hän haluaa olla myös pesäpallo-ottelussa. Korvatakseen pelistä hänelle koituvan edun, Naisen on oltava useammin baletissa.
Vastaavasti, jotta Nainen satunnaistaisi, Naisen on saatava yhtäläinen hyöty menemisestä pesäpallopeliin ja menemisestä balettiin, mikä edellyttää 2q = 3 – 2q eli q = ¾. Näin ollen todennäköisyys, että mies menee pesäpallopeliin, on ¾, ja hän menee balettiin ¼ ajasta. Nämä ovat toisistaan riippumattomia todennäköisyyksiä, joten saadaksemme todennäköisyyden, että molemmat menevät pesäpallo-otteluun, kerromme todennäköisyydet, jolloin saadaan 3/16. Kuvio 16.17 ”Sekastrategian todennäköisyydet” täyttää todennäköisyydet kaikille neljälle mahdolliselle lopputulokselle.
Kuvio 16.17 Sekastrategian todennäköisyydet
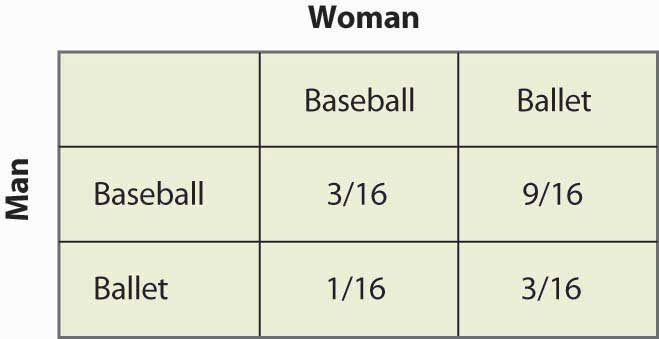
Huomaa, että yli puolet ajasta (Pesäpallo, Baletti) on sekastrategian lopputulos, eivätkä nämä kaksi henkilöä ole yhdessä. Tämä koordinoinnin puute on yleensä sekastrategiatasapainojen ominaisuus. Molempien pelaajien odotetut voitot ovat myös helposti laskettavissa. Miehen voitto on 1 + 2p = 2 – 2p, ja koska p = ¼, mies saa 1½. Samanlainen laskutoimitus osoittaa, että naisen voitto on sama. Molemmat pärjäävät siis huonommin kuin yhteensovittaminen vähemmän mieluisassa lopputuloksessa. Mutta tämä sekastrategian Nash-tasapaino, niin epätoivottavalta kuin se tuntuukin, on Nash-tasapaino siinä mielessä, että kumpikaan osapuoli ei voi parantaa omaa voittoaan, kun otetaan huomioon toisen osapuolen käyttäytyminen.
Sukupuolten välisessä taistelussa sekastrategian Nash-tasapaino voi tuntua epätodennäköiseltä; ja voisimmekin olettaa, että pariskunta koordinoi tehokkaammin. Itse asiassa yksinkertaisen puhelinsoiton pitäisi sulkea pois sekastrategia. Tarkastellaan siis toista sukupuolten taisteluun liittyvää peliä, jossa koordinoinnin epäonnistuminen on järkevämpää. Tämä on peli ”kana”. Tässä pelissä kaksi pelaajaa ajaa toisiaan kohti yrittäen saada toisen väistämään ja lopulta väistämään ojaan. Jos molemmat ajautuvat ojaan, tulos on tasapeli ja molemmat saavat nollan. Jos toinen väistää ja toinen ei, väistävä kuljettaja häviää ja toinen voittaa, ja annamme voittajalle yhden pisteen.Huomaa, että vakion lisääminen pelaajan voittoihin tai pelaajan voittojen kertominen positiivisella vakiolla ei vaikuta Nash-tasapainoihin – puhtaisiin tai sekamuotoisiin. Voimme siis aina antaa kunkin pelaajan yhden tuloksen olla nolla ja toisen tuloksen olla yksi. Ainoa jäljellä oleva kysymys on, mitä tapahtuu, kun kumpikaan ei tuota, jolloin seurauksena on romahdus. Tässä versiossa voitto on asetettu nelinkertaiseksi väistämisestä aiheutuvaan tappioon verrattuna, kuten kuvassa 16.18 ”Kana” näkyy, mutta voit muuttaa peliä ja katsoa, mitä tapahtuu.
Kuva 16.18 Kana
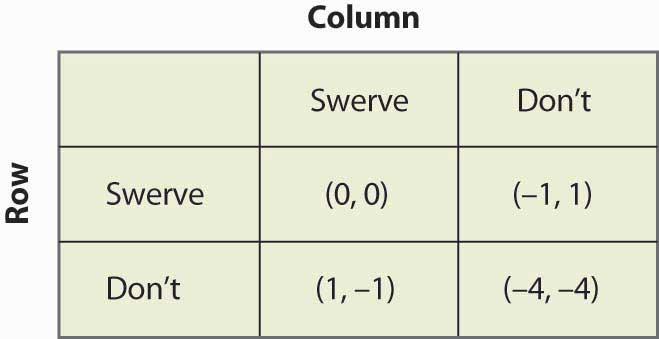
Tässä pelissä on kaksi puhtaan strategian tasapainoa: (Swave, Don’t) ja (Don’t, Swave). Lisäksi siinä on sekastrategia. Oletetaan, että Sarake väistää todennäköisyydellä p. Silloin Rivi saa 0p + -1(1 – p) väistämisestä, 1p + (-4)(1 – p) väistämättä jättämisestä, ja Rivi satunnaistaa, jos nämä ovat yhtä suuret, mikä edellyttää p = ¾. Toisin sanoen todennäköisyys sille, että sarake väistää sekastrategiatasapainossa, on ¾. Voit todentaa, että rivipelaajalla on sama todennäköisyys asettamalla todennäköisyyden, että Rivi väistää, arvoksi q ja laskemalla Sarakkeen odotetut voitot. Törmäyksen todennäköisyys on siis 1/16 sekastrategiatasapainossa.
Sekastrategiatasapaino on jossakin mielessä todennäköisempi tässä pelissä: Jos pelaajat tietäisivät jo valmiiksi, kuka antaa periksi, heidän ei oikeastaan tarvitsisi pelata peliä. Koko pelin tarkoitus on selvittää, kuka antaa periksi, eli sitä ei tiedetä etukäteen. Tämä tarkoittaa, että sekastrategiatasapaino on jossakin mielessä järkevämpi tasapaino.
Kuvio 16.19 Kivi, paperi, sakset
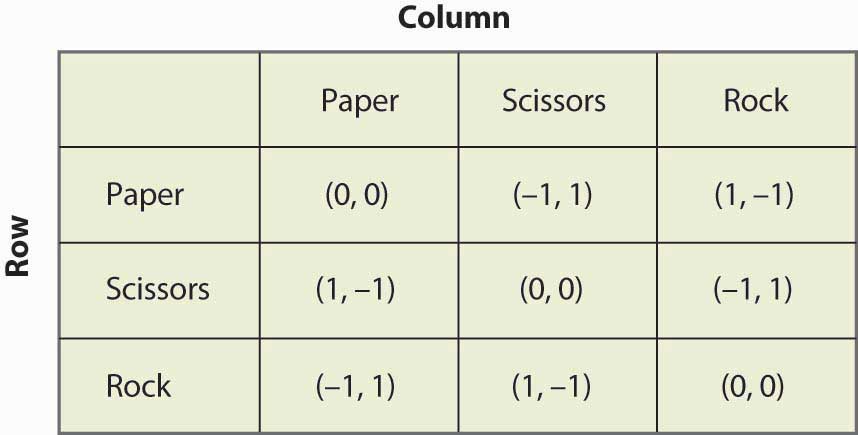
”Kivi, paperi, sakset” on lasten leikki, jossa kaksi lasta käyttää käsiään valitakseen samanaikaisesti paperin (kättä pidetään litteänä), sakset (kädessä on kaksi sormea ulkonevina, jotta se näyttäisi saksilta), tai kiven (kättä pidetään nyrkissä). Voittojen luonne on se, että paperi voittaa kiven, kivi voittaa sakset ja sakset voittaa paperin. Tämä peli on rakenteeltaan sellainen kuin kuvassa 16.19 ”Kivi, paperi, sakset”.
Key Takeaways
- Sekastrateginen Nash-tasapaino edellyttää, että vähintään yksi pelaaja pelaa satunnaistettua strategiaa eikä yksikään pelaaja pysty kasvattamaan odotettavissa olevaa voittoaan pelaamalla vaihtoehtoista strategiaa.
- Nash-tasapainoa, jossa ei käytetä satunnaistamista, sanotaan puhtaan strategisen tason (pure strategy Nash) tasapainoksi.
- Jos pelaajan oletetaan satunnaistavan kahta strategiaa, molempien on tuotettava sama odotettu voitto.
- Penttien yhteensovittamispelissä on sekastrategia eikä yhtään puhdasta strategiaa.
- Sukupuolten taistelu -pelissä on sekastrategia ja kaksi puhdasta strategiaa.
- Kana-peli on samanlainen kuin sukupuolten taistelu ja sillä on sen tavoin kaksi puhdasta strategiaa ja yksi sekastrategia.
Harjoituksia
- Olkoon q todennäköisyys sille, että Rivi pelaa Kruuna. Osoita, että Sarake on halukas satunnaistamaan, jos ja vain jos q = ½. (Vihje: Laske ensin Sarakkeen odotettu voitto, kun Sarake pelaa päätä, ja laske sitten Sarakkeen odotettu voitto, kun Sarake pelaa klaavaa. Näiden on oltava yhtä suuret, jotta Column satunnaistaisi.)
- Osoita, että kivi, paperi, sakset -pelissä ei ole puhtaan strategian tasapainoja. Osoita, että kaikkien kolmen toiminnan pelaaminen yhtä suurella todennäköisyydellä on sekastrategiatasapaino.
-
Löydä seuraavien pelien kaikki tasapainot:
Kuvio 16.20
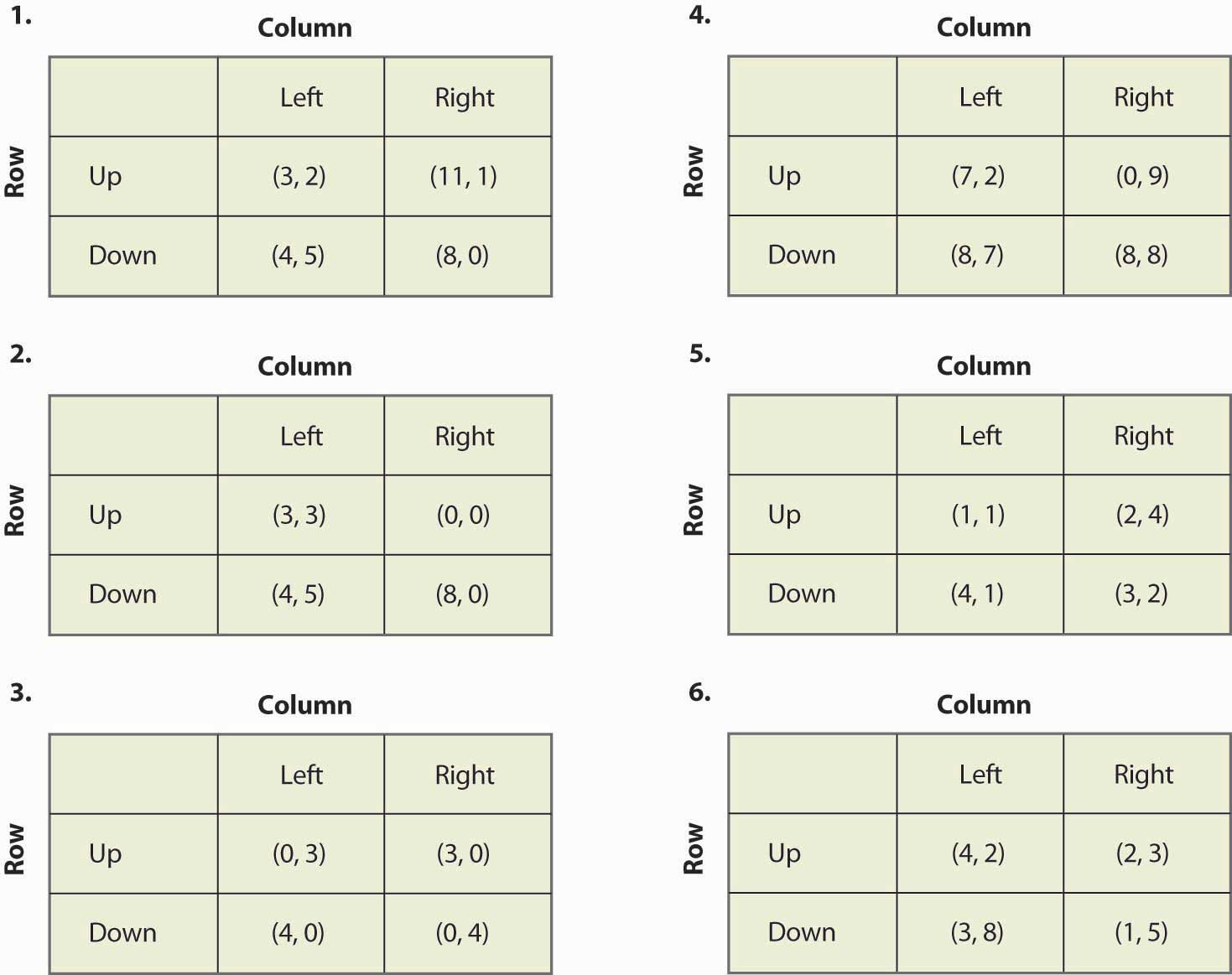
- Jos pelaajan voitto kerrotaan positiivisella vakiolla, pelin tasapainot eivät muutu. Onko tämä totta vai väärin ja miksi?