Talking in Three Dimensions

Katsokaa tätä kuvaa suorakulmaisesta prismasta:

Miten monta kärkeä siinä on? 8

Miten monta reunaa? 12

Miten monta sivua? 6

Helppoa, eikö?

Kokeillaan toista. Katsokaa tätä kuvaa kartiosta:

Miten monta kärkeä sillä on? Lasketaanko huipulla oleva piste?

Miten monta reunaa? Hmm, en ole varma. Eikö reunojen pitäisi olla suoria?

Miten monta pintaa? Se on helppoa! Yksi. Alareunassa on pyöreä pinta. Mutta se ei ole monikulmio, joten onko se silti pinta? Ai niin, ja miksi kutsun kartion toista pintaa? Eikö pintojen tarvitse olla tasaisia?

Yleinen kysymys, jonka saamme 1., 2. ja 3. luokan opettajilta, liittyy siihen, miten kuvata tiettyjen kolmiulotteisten kappaleiden, erityisesti sylinterien ja kartioiden, ominaisuuksia. TEKS:n mukaan oppilaiden pitäisi kuvata kolmiulotteisia kiinteitä aineita käyttämällä muodollista geometrista kieltä, kuten kärkeä, reunaa ja pintaa. Ongelmana on se, että yritämme käyttää kieltä, joka toimii yhdessä muotoluokassa, kuvaamaan aivan toisen luokan ominaisuuksia.

Kolmiulotteiset muodot, kuten prismat ja pyramidit, ovat polyedrejä. ”Geometriassa polyedri on yksinkertaisesti kolmiulotteinen kiinteä kappale, joka koostuu monikulmioiden kokoelmasta, jotka on yleensä yhdistetty reunoistaan.” (Lähde) Näillä kiinteillä kappaleilla on ”litteät monikulmionmuotoiset pinnat, suorat reunat ja yhteiset kulmat tai kärkipisteet”.” (Lähde)

Pallot, sylinterit ja kartiot sen sijaan eivät ole polyedrejä. Tästä johtuen emme voi käyttää täsmälleen samaa kieltä niiden kuvaamiseen, tai jos käytämme samaa kieltä, se tapahtuu sillä ymmärryksellä, että määritelmät eivät ole identtisiä. Otetaan esimerkiksi sana kärki.

Suorakulmaisessa prismassa kärki on terävä piste tai kulma, jossa reunat kohtaavat. Suorakulmaisessa prismassa on 8 kärkeä.

Mutta samaa termiä voidaan käyttää myös kuvaamaan kartion kärkeä. Sama termi, mutta ei sama määritelmä. Kuten Dr. Math sanoo,

Todella hankalaa tässä on se, että kartion ”kärjellä” ei ole mitään tekemistä reunojen kanssa, joten se tarvitsee kokonaan uuden määritelmän; enkä keksi oikein hyvää alkeistason määritelmää sille, mitä ilmeisesti tarkoitetaan, eli yksinkertaisesti ”pisteelle”.

Kun oppilaat harrastavat edistyneempää matematiikkaa, he voivat kehittää hienostuneempaa kieltä ja hienostuneempia määritelmiä. Sillä välin, kun he ovat peruskoulussa, käytämme RRISD:ssä termiä kartion huippu kuvaamaan tätä kartion ominaisuutta.

Jos haluamme, että oppilaat kuvaavat ja luokittelevat tällaista kolmiulotteista kiinteää ainetta, meidän on tarjottava helppokäyttöistä kieltä tätä tarkoitusta varten.

Entä kartion muut ominaisuudet? Tavoitteenamme on jälleen tarjota kieli, joka on alkeisoppilaille ymmärrettävää ja kuvailevaa näistä ominaisuuksista, ja tunnustaa, että oppilaat kehittävät muodollisemman ymmärryksen myöhemmin koulu-uransa aikana. Kartiota kuvaillaksemme sanoisimme, että sillä on pyöreä pohja eli tasainen pinta, jonka päällä kartio lepää. Sanomme myös, että sillä on kaareva reuna pohjaa pitkin ja kaareva pinta, joka ulottuu tästä reunasta kärkeen asti.

Entä sylinteri? Nyt kun meillä on käytössämme kieli, jolla voimme kuvata kartion ominaisuuksia, voimme laajentaa tätä kieltä kuvaamaan sylinterin ominaisuuksia.

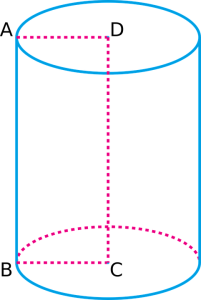
Yllä oleva sylinteri koostuu kahdesta pyöreästä pohjasta, joista toinen on ylhäällä ja toinen alhaalla. Sillä on myös kaksi kaarevaa reunaa, toinen ylhäällä ja toinen alhaalla. Lopuksi sillä on kaareva pinta, joka ulottuu alareunasta yläreunaan asti.

Lisään vielä, että sekä kuvaamani kartio että sylinteri ovat oikeanpuoleinen ympyräkartio ja oikeanpuoleinen sylinteri. Kuten monikulmioista ja moniotteista, myös näistä muodoista on monenlaisia muitakin esimerkkejä. Esimerkiksi kartio tai sylinteri voi olla vinossa, jolloin ne ovat vinoja.

On tärkeää, että oppilaat näkevät erilaisia esimerkkejä kaksi- ja kolmiulotteisista kuvioista. Mitä enemmän he kohtaavat, sitä enemmän he joutuvat kohtaamaan määritelmiä ja terminologiaa, mikä vahvistaa heidän ymmärrystään ominaisuuksista ja siitä, miten ne auttavat meitä tunnistamaan ja luokittelemaan näitä kuvioita.

Miltä tämä näyttää STAAR-testissä?

Vuonna 2016 julkaistussa STAAR-testissä kysyttiin kysymys, joka käsitteli juuri tätä aihetta, ja se vahvisti RRISD:ssä käyttämäämme sanastoa.

Oikea vastaus on: F Niillä ei ole kärkikohtia. Jos katsot joukkoa B, huomaat, että se sisältää kartion, jolla, kuten aiemmin keskustelimme, on huippu. Jos Teksasin opetusvirasto ei käyttäisi termiä kartion huippu, olisimme todennäköisesti nähneet kartion sisältyvän joukkoon A.

Tohtori Mathin loppuajatus:

Mitä määritelmää käytät, riippuu siitä, mitä aiot tehdä sillä. Jos kuvaat vain objekteja, löyhä määritelmäni on hyvä. Jos aiot todistaa tasoja ja kulmia sisältäviä teoreemoja, sinun kannattaa rajoittua monikulmioiden määritelmään, mutta silloin et esitä kysymyksiä kartioista. Luulen, että ihmiset eivät useinkaan ymmärrä, että vaikka matematiikassa ollaan tarkkoja määritelmistä, määritelmät vaihtelevat eri aloilla, koska ne on mukautettu tiettyyn asiayhteyteen. Siihen yritän tässä pyrkiä.

Juuri tähän pyrin.