A proton tömegének feltárása

APS/Alan Stonebraker

APS/Alan Stonebraker

Az ismert anyag szinte teljes tömege a protonokban és neutronokban található – azokban a részecskékben, amelyek az atommagokat alkotják. De hogyan jutnak tömegükhöz a protonok és a neutronok? Mindegyik részecske, vagy “nukleon”, más részecskék sűrű, habos kuszaságából áll: kvarkokból, amelyeknek van tömegük, és gluonokból, amelyeknek nincs. A kvarkok tömege azonban a proton vagy neutron tömegének csupán 1%-át teszi ki, a proton tömegének nagy része pedig pusztán a kvarkok és gluonok mozgásából és összezártságából származik. Yi-Bo Yang (Michigan State University, East Lansing) és munkatársai most először számszerűsítették a proton tömegéhez való négy különálló hozzájárulást a kvantumkromodinamikán (QCD) alapuló számítással, amely az erős kölcsönhatás alapvető elmélete az atommagban, és a részecskefizika standard modelljének egyik sarokköve. Bár ez a négy részre bontás már több mint 20 éve ismert , a fizikusok megértése eddig csak minőségi volt.

A proton és a neutron alkotó kvarkok alapvető részecskék, amelyek tömegüket a Higgs-mechanizmus révén kapják. Ugyanez a mechanizmus nem magyarázza a proton tömegét, amely két up kvarkból ( egyenként 2,4MeV∕c2 ) és egy down kvarkból ( 5,0MeV∕c2 ) áll . Nyilvánvaló, hogy e három tömeg összege messze elmarad a proton tényleges tömegétől, amely 938,27MeV∕c2. A kvantummechanika szerint a kvarkoknak a protonba való bezáródásához is kapcsolódik tömeg (vagy ennek megfelelő energia), amelynek átmérője kb. 10-15 m. A kvarkok tömegét a kvantummechanika szerint a protonba való bezáródásához is kapcsolódik tömeg (vagy ennek megfelelő energia). A bizonytalansági elv szerinti érvelés alapján a részecskék bezárt helyzete nagy impulzust eredményez, és körülbelül 300MeV∕c2-t kellene hozzáadnia – ami megfelel a proton tömegének, de még mindig túl kicsi. (Hasonló érvek vonatkoznak a neutronra is, amely két down kvarkból és egy up kvarkból áll.)

Tény, hogy a standard modell pontos előrejelzései mind a proton, mind a neutron tömegére vonatkozóan már egy évtizede léteznek. Az atommag szempontjából releváns alacsony energiákon ezek a tömegek mindössze három paraméterből jósolhatók meg: egy általános tömegskálából, amely a QCD-ben dinamikusan keletkezik, valamint a felfelé és lefelé kvarkok paramétereiből. A protonok és neutronok tömegét sokkal pontosabban ismerjük a kísérletekből, mint ahogyan azt a standard modell előrejelzései valaha is lehetővé teszik. A fizikusok azonban szeretnék megérteni, hogyan keletkeznek a tömegek a QCD-ből, hasonlóan ahhoz, ahogyan a kvantumelméletből meg tudják jósolni a hidrogén spektrumát.

Yang és munkatársai éppen ezt tették, és először határozták meg a proton tömegéhez való különböző hozzájárulásokat, amelyek a kvarkok és gluonok dinamikájából származnak . A kutatók a rács QCD néven ismert nagy teljesítményű módszerre támaszkodnak, amely a kvarkokat egy rács oldalaira, a gluonokat pedig a köztük lévő kapcsolatokra helyezi. A QCD e szigorú ábrázolása numerikusan is megvalósítható, és ez az egyetlen QCD-alapú módszer, amely képes kvantitatív előrejelzéseket tenni a protonhoz hasonló vagy annál nagyobb hosszskálákon. (Ezeken a léptékeken a kvarkok és gluonok közötti kölcsönhatások olyan erősek, hogy nem kezelhetők Feynman-diagramokkal és más “perturbatív” módszerekkel). A rácsos QCD azonban drága technika. A diszkretizálás hibákat okoz, és ezek kiküszöbölése azt jelenti, hogy a rácstávolságot, az a-t, nullára kell csökkenteni. Ezt a lépést a gyakorlatban úgy érik el, hogy többszörös számításokat végeznek az a különböző értékeinél, ami nagy numerikus költséggel jár, amely a-6 értékkel skálázódik. Mindazonáltal a rács QCD az elmúlt években jelentősen kiforrott, lehetővé téve a kvarkok tömegének és a könnyű és nehéz mezonok , amelyek egy kvarkból és egy antikvarkból állnak, számos tulajdonságának legpontosabb meghatározását.

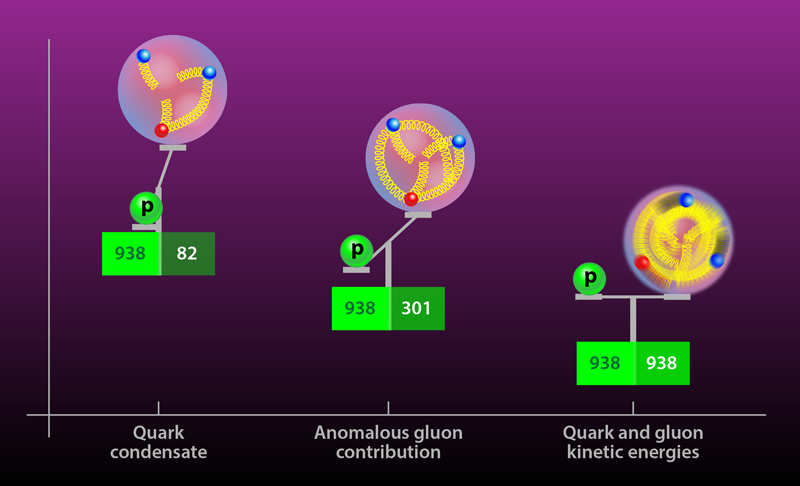
A három kvarkból álló részecske, mint a nukleon, exponenciálisan bonyolultabb a rács QCD számára, és a sikeres, minden bizonytalansági forrást kontrollált számítások ritkák voltak. Munkájukban Yang és munkatársai az általuk és másokkal együtt kifejlesztett új számítási módszerek alkalmazásával leküzdötték a bonyodalmak egy részét. Ezek a fejlesztések lehetővé tették számukra, hogy kiszámítsák a proton tömegéhez való hozzájárulást négy forrásból, amelyek a kvarkkondenzátum ( ∼9%), a kvarkenergia ( ∼32%), a gluonikus térerősség energiája ( ∼37%) és az anomális gluonikus hozzájárulás ( ∼23%) (1. ábra). A legkisebb hozzájárulás, a kvarkkondenzátum, a felfelé és lefelé mutató kvarkok és a virtuális furcsa kvarkok “tengerének” keveréke, és ez az egyetlen, amely eltűnne, ha a kvarktömegek nulla lennének. A másik három tag mind a kvarkok és gluonok dinamikájához és a protonon belüli bezártságukhoz kapcsolódik. A kvarkenergia és a gluon térerősség a bezárt kvarkok, illetve a bezárt gluonok mozgási energiájának felel meg. Az anomális kifejezés tisztán kvantumhatás. A QCD tömegskálához kapcsolódik, és az összes kvark-íz kondenzátumának hozzájárulásaiból áll, beleértve a furcsa, bűvös, alsó és felső kvarkokat is. Yang és munkatársai számításai azt mutatják, hogy ha a felfelé, lefelé és furcsa kvarkok tömege mind nulla lenne, a proton még mindig a kísérleti tömegének több mint 90%-ával rendelkezne. Más szóval, az Univerzum szinte minden ismert tömege a kvarkok és gluonok dinamikájából származik.

A fizikusok régóta szeretnék megérteni a nukleon tömegének kialakulását a standard modell szempontjából, és Yang és munkatársai eredményei fontos hozzájárulást jelentenek ehhez a célhoz. Munkájuk és más hasonló munkák egy új korszakot is jeleznek, amelyben a nukleonokkal kapcsolatos ismereteinket egyre inkább a rácsos QCD-n alapuló kvantitatív előrejelzések alakítják. Éppen ebben az évben a kutatók a rácsos QCD-t használták a nukleonok tengelytöltésének – a magfizikában mindenütt jelenlévő mennyiségnek – a meghatározására, mégpedig példátlan, 1%-os pontossággal. A rácsos QCD a QCD-számítások egyszerűsítésére szolgáló hatékony analitikus módszerekkel párosulva a nukleon szubstruktúrájának jobb megértéséhez fog vezetni, amelyet a világ különböző ütköztetőiben vizsgálnak, és amely az elektron-ion ütköztetőnek nevezett tervezett gép egyik fókuszpontja lenne. Végső soron a remény az, hogy a rácsos QCD-t alkalmazni lehet egy atommagra (több nukleonra). Az atommagokat detektorokként használják számos, a standard modellen túli fizika kísérleti kutatásában, mint például a sötét anyag, az állandó elektromos dipólusmomentum és a neutrinol nélküli kettős béta-bomlás. E kísérletek értelmezéséhez a standard modellben gyökerező magfizika kvantitatív megértése szükséges. Ez a fajta összetett probléma egyre inkább a rácsos QCD birodalmába kerül, köszönhetően a közel exascale számítógépek, a Sierra és a Summit elérhetőségének, amelyek most kerülnek üzembe, és 10-15-ször erősebbek még a Yang és munkatársai által használtaknál is.

Ez a kutatás a Physical Review Letters-ben jelent meg.

1. Y.-B. Yang, J. Liang, Y.-J. Bi, Y. Chen, T. Draper, K.-F. Liu, and Z. Liu, “Proton mass decomposition from the QCD energy momentum tensor,” Phys. Rev. Lett. 121, 212001 (2018).
2. X.-D. Ji, “QCD analysis of the mass structure of the nucleon,” Phys. Rev. Lett. 74, 1071 (1995).
3. S. Aoki et al., “Review of lattice results concerning low-energy particle physics,” Eur. Phys. J. C 77, 112 (2017); A kvarkoknak nincs tömegük abban az értelemben, mint az elektronnak. De a kvarkok tömegparamétere mégis szigorúan meghatározható egy meghatározott renormálási sémával és skálával. Az Aoki et al. által idézett tömegek az úgynevezett MS-bar sémában 2 GeV-os skálán vannak.
4. S. Durr et al., “Ab initio determination of light hadron masses,” Science 322, 1224 (2008).
5. A. Bazavov et al., “Up-, down-, strange-, charm-, and bottom-quark masses from four-flavor lattice QCD,” Phys. Rev. D 98, 054517 (2018).
6. K-F. Liu, J. Liang, and Y.-B, Yang, “Variance reduction and cluster decomposition,” Phys. Rev. D 97, 034507 (2018).
7. Y.-B. Yang, M. Gong, J. Liang, H.-W. Lin, K.-F. Liu, D. Pefkou és P. Shanahan, “Nonperturbatively renormalized glue momentum fraction at the physical pion mass from lattice QCD,” Phys. Rev. D 98, 074506 (2018).
8. Y.-B. Yang, R. Sufian, A. Alexandru, T. Draper, M.J. Glatzmaier, K.-F. Liu, and Y. Zhao, “Glue spin and helicity in the proton from lattice QCD,” Phys. Rev. Lett. 118, 102001 (2017).
9. C. C. Chang et al., “A per-cent-level determination of the nucleon axial coupling from quantum chromodynamics,” Nature 558, 91 (2018).
10. H.-W. Lin et al., “Partoneloszlások és rácsos QCD számítások: A community white paper,” Prog. Part. Nucl. Phys. 100, 107 (2018).

A szerzőről

André Walker-Loud a Lawrence Berkeley National Laboratory (LBNL) tudományos munkatársa. Doktori fokozatát a seattle-i Washingtoni Egyetemen szerezte. Ezt követően posztdoktori kutatói állásokat töltött be a Marylandi Egyetemen, a The College of William & Mary (W&M) és az LBNL-ben, majd a W&M-ben a fizika adjunktusaként és a Thomas Jefferson National Accelerator Facility vezető munkatársaként dolgozott. Kutatásai során a rácsos QCD-t és az effektív mezőelméletet használja annak kvantitatív megértésére, hogy a QCD-ből hogyan jön létre a magfizika. Érdeklődik továbbá a standard modell határainak feltárása iránt az alapvető szimmetriák nukleáris környezetben történő tesztelésével.

Témakörök

További cikkek