Bevezetés
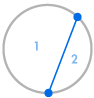
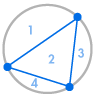
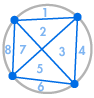
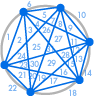
Tegyük fel, hogy egy kör kerületén több pontot helyezünk el, és minden pontot összekötünk egymással. Ezáltal a kört sok különböző területre osztjuk, és minden esetben meg tudjuk számolni a területek számát. Az alábbi ábrák azt mutatják, hogy hány régió van a kerület több különböző számú pontja esetén. Arra kell ügyelnünk, hogy a körön belül minden metszéspontban csak két egyenes találkozzon, ne három vagy több.
 |
 |
 |
 |
 |
| 1 régió | 2 régió | 4 régió | 8 régió | 16 régió |
Máris láthatunk egy mintát: A régiók száma mindig kétszerese az előzőnek, így kapjuk az 1, 2, 4, 8, 16, … sorozatot. Ez azt jelenti, hogy a kerület 6 pontjával 32 régió lenne, 7 pontjával pedig 64 régió.
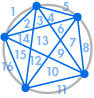
Eldönthetjük, hogy elégedettek vagyunk ezzel az eredménnyel. A régiók száma mindig kétszerese az előzőnek – elvégre az első öt esetben ez működött. Vagy úgy dönthetünk, hogy a biztonság kedvéért még néhányat ellenőrizzünk:
 |
 |
| 31 régió, nem 32 | 57 régió, nem 64 |
Szerencsétlenségünkre valami rosszul sikerült: 31 talán számolási hibának tűnik, de 57 sokkal kevesebb, mint 64. A sorozat 99, 163, 256, … folytatódik, egészen másként, mint amit az előző szám megduplázásakor kapnánk.
Ez a példa jól szemlélteti, hogy a matematikában miért nem mondhatjuk, hogy egy megfigyelés mindig igaz, csak azért, mert néhány kipróbált esetben működik. Ehelyett egy szigorú logikai érveléssel kell előállnod, amely a már ismert eredményekből elvezet valami újhoz, amiről be akarod mutatni, hogy igaz. Az ilyen érvelést nevezzük bizonyításnak.
A bizonyítások különböztetik meg a matematikát az összes többi tudománytól, mert ha egyszer bebizonyítottunk valamit, akkor teljesen biztosak lehetünk benne, hogy az igaz, és mindig igaz lesz. Nem csak egy elméletről van szó, amely megfelel a megfigyeléseinknek, és amelyet a jövőben egy jobb elmélet válthat fel.
A fenti példában megszámolhatnánk a kör belsejében lévő metszéspontok számát. Ha alaposan átgondoljuk a metszéspontok, a vonalak és a régiók száma közötti kapcsolatot, akkor végül egy másik egyenlethez jutunk a régiók számának kiszámítására, ha van x = V.Axi pontok a körön:
Régiók száma = x4 – 6 x3 + 23 x2 – 18 x + 2424 = (Math.pow(V.Axi,4) – 6*Math.pow(V.Axi,3) + 23*Math.pow(V.Axi,2) – 18*V.Axi + 24)/24.
Ez az egyenlet minden fenti esetben működik. Most megpróbálhatjuk bizonyítani x minden értékére az “indukció” segítségével, amely technikát alább ismertetjük.
Hagyományosan a bizonyítás végét egy ■ vagy □ jelöli, vagy a QED vagy “quod erat demonstrandum” írásmóddal, ami latinul azt jelenti, hogy “amit meg kellett mutatni”.
Egy eredményt vagy megfigyelést, amelyet igaznak gondolunk, hipotézisnek vagy sejtésnek nevezünk. Ha egyszer bebizonyítottuk, Tételnek nevezzük. Ha egyszer bebizonyítottunk egy tételt, felhasználhatjuk más, bonyolultabb eredmények bizonyítására – így a matematikai tételek egyre növekvő hálózatát építhetjük ki.
Axiomok

Raffael athéni iskolája: Az ókori görög matematikusok voltak az elsők, akik a matematikát logikai és axiomatikus keretrendszer segítségével közelítették meg.
Egy érdekes kérdés, hogy honnan induljunk ki. Hogyan bizonyítod az első tételt, ha még semmit sem tudsz? Sajnos a semmiből nem lehet valamit bizonyítani. Szükséged van legalább néhány építőelemre, amiből kiindulhatsz, és ezeket axiómáknak nevezik.
A matematikusok feltételezik, hogy az axiómák igazak, anélkül, hogy be tudnák bizonyítani őket. Ez azonban nem olyan problematikus, mint amilyennek látszik, mert az axiómák vagy definíciók, vagy egyértelműen nyilvánvalóak, és csak nagyon kevés axióma létezik. Egy axióma lehet például az, hogy a + b = b + a bármely két a és b számra.
Az axiómákat fontos helyesnek tartani, mert az egész matematika ezeken alapul. Ha túl kevés axióma van, akkor nagyon keveset tudunk bizonyítani, és a matematika nem lenne túl érdekes. Ha túl sok axióma van, akkor szinte bármit be tudsz bizonyítani, és a matematika szintén nem lenne érdekes. Az axiómák sem lehetnek egymásnak ellentmondóak.
A matematika nem az axiómák megfelelő halmazának kiválasztásáról szól, hanem arról, hogy ezekből a kiindulópontokból kialakítsunk egy keretrendszert. Ha más axiómákkal indulsz, másfajta matematikát kapsz, de a logikai érvek ugyanazok lesznek. A matematika minden területének megvan a maga alapaxiómakészlete.
Amikor a matematikusok bebizonyítottak egy tételt, közzéteszik, hogy más matematikusok ellenőrizhessék. Néha hibát találnak a logikai érvelésben, néha pedig csak sok évvel később derül ki a hiba. Elvileg azonban mindig lehetséges egy bizonyítást az alapvető axiómákra lebontani.
A halmazelmélet és a választás axiómája

A bizonyítások megfogalmazásához néha vissza kell nyúlni annak a nyelvnek az alapjaihoz, amelyen a matematikát írjuk: a halmazelmélethez.
A halmaz objektumok, például számok gyűjteménye. A halmaz elemeit általában szögletes zárójelben írjuk. Megkereshetjük két halmaz unióját (azon elemek halmazát, amelyek bármelyik halmazban benne vannak) vagy két halmaz metszetét (azon elemek halmazát, amelyek mindkét halmazban benne vannak).
Sok matematikai probléma a halmazelmélet nyelvén fogalmazható meg, és bizonyításukhoz halmazelméleti axiómákra van szükségünk. Az idők során a matematikusok különböző axiómagyűjteményeket használtak, a legelterjedtebb a kilenc Zermelo-Fraenkel (ZF) axióma:
A Kiterjedés axiómája
Ha két halmaznak ugyanazok az elemei, akkor egyenlőek.
ALKALMAZÁSAXIOMJA
Egy halmazból képezhetünk olyan részhalmazt, amely bizonyos elemekből áll.

EGYENES TELJESSÉG AXIOM
Létezik olyan halmaz, amelynek nincsenek tagjai, ezt {} vagy ∅ alakban írjuk.
KÖZÖSSÉG AXIOM
Megadva két x és y objektumot, alkothatunk egy {x, y} halmazt.
UNION AXIOM
Két vagy több halmaz unióját alkothatjuk.
TÖRÖKKÖZET AXIOM
Minden halmazból képezhetjük az összes részhalmaz halmazát (a hatványhalmazt).
VÉGTELENSÉGAXIOM
Létezik olyan halmaz, amelynek végtelen sok eleme van.

AXIOM OF FOUNDATION
A halmazok egyszerűbb halmazokból épülnek fel, ami azt jelenti, hogy minden (nem üres) halmaznak van egy minimális tagja.
A KIEGÉSZÍTÉSAXIÓMÁJA
Ha egy halmaz minden elemére alkalmazunk egy függvényt, a válasz még mindig egy halmaz marad.
Ha a halmazelméletre gondolunk, a legtöbb axióma teljesen nyilvánvalónak fog tűnni – és az axiómáknak éppen ez a dolguk. Van azonban egy tizedik axióma, amely meglehetősen problematikusabb:
VÁLASZTÁSAXIÓMA
Elvéve végtelen sok nem üres halmazt, mindegyik halmazból választhatunk egy-egy elemet.
Előső látásra a választás axiómája (AC) ugyanolyan ártatlannak tűnik, mint a többi fenti. A végtelenség használata azonban számos váratlan következménnyel jár. Például az AC segítségével bebizonyíthatjuk, hogy lehetséges egy gömböt öt darabra vágni, majd újra összerakni, hogy két, a kiindulási gömbbel azonos gömböt kapjunk. Ez csak egy elméleti elképzelés – a szükséges darabok fraktálisak, ami azt jelenti, hogy a valóságban nem létezhetnek, és néhány darab “nem mérhető”, ami azt jelenti, hogy nincs meghatározott térfogatuk. De az a tény, hogy a választás axiómája felhasználható ezeknek a lehetetlen vágásoknak a megkonstruálására, eléggé aggasztó.
A logikusok között szenvedélyes vita folyik arról, hogy elfogadjuk-e a választás axiómáját vagy sem. Az axiómák minden gyűjteménye egy kis “matematikai világot” alkot, és különböző világokban különböző tételek lehetnek igazak. Igazából csak az a kérdés, hogy örülsz-e annak, hogy olyan világban élsz, ahol egyből két gömböt tudsz csinálni…
Bizonyítás indukcióval
Az indukciós bizonyítás olyan technika, amellyel bebizonyítható, hogy egy bizonyos állítás igaz minden természetes számra 1, 2, 3, … Az “állítás” általában egy egyenlet vagy képlet, amely tartalmaz egy n változót, amely lehet bármilyen természetes szám. Jelöljük az n-re alkalmazott állítást S(n)-nel. Íme a matematikai indukció négy lépése:
- Először bebizonyítjuk, hogy S(1) igaz, vagyis hogy az S állítás igaz 1-re.
- Most feltételezzük, hogy S(k) igaz, vagyis hogy az S állítás igaz valamilyen k természetes számra.
- Ezt a feltételezést felhasználva megpróbáljuk levezetni, hogy S(k + 1) is igaz. Tehát valahányszor S igaz egy számra, az igaz a következő számra is.
- Mivel tudjuk, hogy S(1) igaz, S(2) is igaz kell, hogy legyen. És ezért S(3) is igaz kell, hogy legyen. És ezért S(4)-nek igaznak kell lennie. És így tovább:

Az indukciót a leeső dominókhoz hasonlíthatjuk: amikor egy dominó leesik, a következő is leesik. Az első lépés, annak bizonyítása, hogy S(1) igaz, elindítja a végtelen láncreakciót.
Az első lépést gyakran figyelmen kívül hagyják, mert olyan egyszerű. Valójában nagyon fontos, és az egész indukciós lánc tőle függ – amint azt néhány alábbi példa is mutatja…
A Towers of Hanoi játék célja, hogy bizonyos számú korongot egyik csapról a másikra helyezzünk. Egyszerre csak egy korongot mozgathatsz, és nem rakhatsz nagyobb korongot egy kisebbre. Próbáld meg a korongokból álló tornyot az első csapról az utolsó csapra mozgatni, a lehető legkevesebb mozdulattal:
Korongok száma: Tárcsák száma: Start Over Moves: Start Over Moves: Start Over Moves: Start Over Moves: 0
Amint megértettük a játékszabályokat, megpróbálhatjuk megtalálni a legkevesebb szükséges lépésszámot, bármilyen számú korong esetén. A fenti játékkal játszva megfigyelhetjük, hogy n korong esetén legalább 2n – 1 lépésre van szükség. Nevezzük ezt az állítást S(n)-nek.
S(1) egyértelműen igaz, hiszen egyetlen koronggal csak egy lépésre van szükségünk, és 21 – 1 = 1.
Most tegyük fel, hogy S(k) igaz, vagyis hogy k korong esetén 2k – 1 lépésre van szükségünk. Akkor ha k + 1 korongunk van:
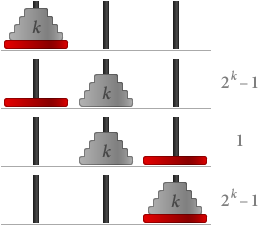
összességében (2k – 1) + 1 + (2k – 1) = 2(k+1) – 1 lépésre van szükségünk. Ez azt jelenti, hogy S(k + 1) is igaz.
Matematikai indukcióval S(n) n minden értékére igaz, ami azt jelenti, hogy n = V.Hanoi korong mozgatásának leghatékonyabb módja 2n – 1 = Math.pow(2,V.Hanoi)-1 lépést igényel. ■
Bizonyítsuk be indukcióval, hogy az első n természetes szám összege n (n + 1)2. Először ellenőrizzük az egyenletet n kis értékeire:
1 = 1 (1 + 1)2.
1 + 2 = 2 (2 + 1)2 = 3.
Ezután feltételezzük, hogy az eredmény k-ra is igaz, vagyis hogy 1 + 2 + … + k = k (k + 1)2, ahol k valamilyen általunk meg nem adott szám. Most
1 + 2 + … + k + (k + 1) = k (k + 1)2 + (k + 1) = (k + 1) (k + 2)2 = (k + 1) 2.
Most bizonyítottuk, hogy ha az egyenlet igaz valamilyen k-ra, akkor igaz k + 1-re is. Matematikai indukcióval az egyenlet n minden értékére igaz. ■
A fenti egyenlet bizonyításának van egy másik okos módja is, amely nem használ indukciót. Állítólag Carl Friedrich Gauss (1777 – 1855), a történelem egyik legnagyobb matematikusa fedezte fel ezt a módszert az általános iskolában, amikor tanára arra kérte, hogy adja össze az összes egész számot 1-től 100-ig.
Az indukciót használva azt akarjuk bizonyítani, hogy minden embernek egyforma a hajszíne. Legyen S(n) az az állítás, hogy “bármely n emberből álló csoportban mindenkinek ugyanolyan a hajszíne”.
Egyértelmű, hogy S(1) igaz: bármely csak egy emberből álló csoportban mindenkinek ugyanolyan a hajszíne.
Most tegyük fel S(k), hogy bármely k emberből álló csoportban mindenkinek ugyanolyan a hajszíne. Ha a csoport bármelyik tagját kicseréljük valakire, akkor is összesen k-an vannak, tehát ugyanolyan a hajszínük. Ez bármelyik kezdeti csoportra működik, vagyis bármelyik k + 1 fős csoportnak is ugyanolyan a hajszíne. Ezért S(k + 1) igaz.
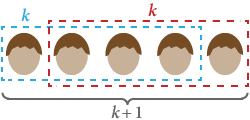
A matematikai indukció alapján minden embernek ugyanolyan a hajszíne! ■
A fenti bizonyításban nyilván valami félrement – elvégre nem mindenkinek egyforma a hajszíne. Meg tudod találni a hibát?
Néhány tételt nem egészen lehet indukcióval bizonyítani – egy kissé módosított változatot, az úgynevezett erős indukciót kell használnunk. Ahelyett, hogy feltételeznénk S(k)-t S(k + 1) bizonyításához, feltételezzük az összes S(1), S(2), … S(k)-t S(k + 1) bizonyításához. Minden, ami (gyenge) indukcióval bizonyítható, nyilvánvalóan bizonyítható erős indukcióval is, de fordítva nem.
A számtan alaptétele kimondja, hogy minden 1-nél nagyobb egész szám vagy prímszám, vagy prímszámok szorzataként írható fel lényegében egyedi módon.
Egy részét erős indukcióval bizonyíthatjuk: legyen S(n) az az állítás, hogy “az n egész szám prímszám vagy prímszámok szorzataként írható fel”. S(1) kivétel, de S(2) egyértelműen igaz, mert 2 prímszám.
Most tegyük fel, hogy S(1), S(2), …, S(k) mind igaz, valamilyen k egész számra. Tudjuk, hogy k + 1 vagy prímszám, vagy k + 1-nél kisebb faktorai vannak. Feltételezésünk alapján tudjuk, hogy ezek a tényezők prímszámok szorzataként írhatók fel. Ezért, hacsak nem prímszám, akkor k + 1 is felírható prímszámok szorzataként. Ez azt jelenti, hogy S(k + 1) igaz.
Erős indukcióval S(n) igaz minden n számra, amely nagyobb 1-nél. ■
Az, hogy bebizonyítsuk, hogy ez a prímtényezős tagolás egyedi (hacsak nem számítjuk a tényezők különböző sorrendjeit), több munkát igényel, de nem különösebben nehéz.
Kiderül, hogy a gyenge indukció és az erős indukció elve egyenértékű: egyik feltételezi a másikat. Mindkettő ekvivalens egy harmadik tétellel is, a jólrendeződési elvvel: a természetes számok bármely (nem üres) halmazának van egy minimális eleme, amely kisebb, mint az összes többi.
A jólrendeződési elv a természetes számok meghatározó tulajdonsága. Ez a természetes számok ![]() = {1, 2, 3, …} meghatározásához használt egyik alapaxióma. Ezeket az axiómákat Peano axiómáknak nevezik, Guiseppe Peano (1858 – 1932) olasz matematikusról elnevezve.
= {1, 2, 3, …} meghatározásához használt egyik alapaxióma. Ezeket az axiómákat Peano axiómáknak nevezik, Guiseppe Peano (1858 – 1932) olasz matematikusról elnevezve.
Az ellentmondásos bizonyítás
Az ellentmondásos bizonyítás egy másik fontos bizonyítási technika. Ha egy S állítást akarunk bizonyítani, feltételezzük, hogy S nem volt igaz. Ezt a feltételezést felhasználva megpróbálunk egy hamis eredményt levezetni, például 0 = 1. Ha minden lépésünk helyes volt, és az eredmény hamis, akkor a kezdeti feltételezésünk biztosan téves volt. A kezdeti feltételezésünk az volt, hogy S nem igaz, ami azt jelenti, hogy S valójában igaz.
Ez a technika sokféle esetben alkalmazható, például annak bizonyítására, hogy √2 irracionális, annak bizonyítására, hogy a valós számok megszámlálhatatlanok, vagy annak bizonyítására, hogy végtelen sok prímszám van.
Itt egy másik szórakoztató példa:
Az ellentmondásos bizonyítással és a jólrendezettség elvével együtt használhatjuk annak bizonyítására, hogy minden természetes szám “érdekes”.
Tegyük fel, hogy nem minden természetes szám érdekes, és legyen S a nem érdekes számok halmaza. A jól rendező elv alapján S-nek van egy legkisebb tagja x, amely a legkisebb nem érdekes szám. Ez a furcsa tulajdonság nyilvánvalóan x-et különösen érdekes számmá teszi. Ez ellentmondás, mert feltételeztük, hogy x nem érdekes.
Ezért minden szám érdekes. ■
Gödel és a bizonyíthatatlan tételek

Kurt Gödel (1906-1978)
A 20. század elején a matematika gyors fejlődésnek indult, matematikusok ezrei dolgoztak számtalan új területen. David Hilbert (1862-1943) kiterjedt programot indított a matematika formalizálására és a matematika alapjainak ellentmondásainak feloldására. Ez magában foglalta az összes tétel bizonyítását egy egyszerű és univerzális axiómakészlet segítségével, annak bizonyítását, hogy ez az axiómakészlet konzisztens, és annak bizonyítását, hogy ez az axiómakészlet teljes, vagyis hogy minden matematikai állítás bizonyítható vagy cáfolható az axiómák segítségével.
Ezeket a terveket sajnos Kurt Gödel 1931-ben megsemmisítette. Ő bebizonyította, hogy bármely (kellően bonyolult) matematikai rendszerben, amely egy bizonyos axiómakészletet tartalmaz, találhatunk olyan állításokat, amelyeket az axiómák segítségével sem bizonyítani, sem cáfolni nem lehet. Azt sem lehet bizonyítani, hogy egy bizonyos axiómakészlet konzisztens, csak magával az axiómákkal.
Gödel felfedezése azon a tényen alapul, hogy egy axiómakészletet nem lehet arra használni, hogy önmagáról bármit is mondjunk, például azt, hogy konzisztens. Az önreferenciával kapcsolatos problémák nemcsak a matematikában, hanem a nyelvben is megtalálhatók. Íme a hazug paradoxon:
“Ez a mondat hamis.”
A fenti mondat megpróbál valamit mondani önmagáról. Ha igaz, akkor a mondat azt mondja, hogy hamis. Ha hamis, akkor a mondat azt mondja nekünk, hogy nem hamis, azaz igaz. A mondat valójában sem nem igaz, sem nem hamis.
Az első publikálásakor Gödel tételei sok matematikust mélyen felkavartak. Amikor egy megfigyelés bizonyítására indulunk, nem tudhatjuk, hogy létezik-e bizonyítás – az eredmény lehet, hogy igaz, de nem bizonyítható. Ma már tudjuk, hogy a befejezetlenség nemcsak a logikának, hanem a logikai műveleteket végző gépekre támaszkodó számítástechnikának is alapvető része.
Meglepő módon bizonyítani lehet, hogy bizonyos állítások bizonyíthatatlanok. Ilyen például a kontinuumhipotézis, amely a végtelen halmazok méretéről szól.
Élete vége felé Kurt Gödel súlyos mentális problémákkal küzdött, és 1978-ban éhen halt. A logika alapjaira vonatkozó meglátásai a legmélyebbek voltak az ókori görögök által kifejlesztett bizonyítás óta.