
Bertrand Russell (1872-1970) és A.N. Whitehead (1861-1947)
Bertrand Russell és Alfred North Whitehead brit matematikusok, logikusok és filozófusok voltak, akik a 20. század elején a kontinentális idealizmus elleni brit lázadás élharcosai voltak, és együttesen jelentős eredményeket értek el a matematikai logika és a halmazelmélet területén.
Whitehead volt kettejük közül az idősebb, és inkább tiszta matematikai háttérrel rendelkezett. Az 1890-es években Russell tanára lett a cambridge-i Trinity College-ban, majd a 20. század első évtizedében együttműködött híresebb volt tanítványával monumentális művükön, a “Principia Mathematica”-on. Az első világháború után azonban – amelynek nagy részét Russell pacifista tevékenysége miatt börtönben töltötte – az együttműködés elhalványult, és Whitehead tudományos karrierje mindvégig az extravagánsabb Russell karrierjének árnyékában maradt. Az 1920-as években az Egyesült Államokba emigrált, és élete hátralévő részét ott töltötte.
Russell a brit arisztokrácia gazdag családjába született, bár szülei a korhoz képest rendkívül liberálisak és radikálisak voltak. Szülei meghaltak, amikor Russell még egészen fiatal volt, és nagyrészt meggyőződéses viktoriánus (bár meglehetősen progresszív) nagyanyja nevelte. Kamaszkora nagyon magányos volt, és depressziós rohamokban szenvedett, később azt állította, hogy csak a matematika iránti szeretete tartotta vissza az öngyilkosságtól. A Cambridge-i Egyetemen tanult matematikát és filozófiát G. E. Moore és A. N. Whitehead mellett, ahol innovatív filozófussá, számos témában termékeny íróvá, elkötelezett ateistává, valamint ihletett matematikussá és logikussá vált. Ma az analitikus filozófia egyik alapítójának tartják, de a filozófia szinte minden jelentős területéről írt, különösen a metafizikáról, az etikáról, az ismeretelméletről, a matematikafilozófiáról és a nyelvfilozófiáról.
Russell hosszú élete során elkötelezett és magas szintű politikai aktivista volt. Mind az első, mind a második világháború idején kiemelkedő háborúellenes aktivista volt, a szabadkereskedelem és az antiimperializmus híve, később pedig a nukleáris leszerelés és a szocializmus, valamint Adolf Hitler, a szovjet totalitarizmus és az USA vietnami háborúban való részvétele ellen folytatott éles kampányt.
Russell paradoxona
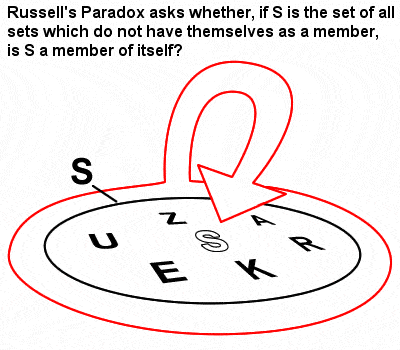
Russell paradoxona
Russell matematikájára nagy hatással volt Gottlob Frege halmazelmélete és logikája, amelyet Cantor úttörő korai halmazelméleti munkája nyomán fejlesztett ki. Az 1903-ban megjelent “A matematika alapelvei” című művében azonban azonosította a mára Russell-paradoxonként ismertté vált jelenséget (olyan halmaz, amely olyan halmazokat tartalmaz, amelyek nem tagjai önmaguknak), amely megmutatta, hogy Frege naiv halmazelmélete valójában ellentmondásokhoz vezethet.
A paradoxont néha ezzel a leegyszerűsített példával illusztrálják: “Ha egy borbély megborotválja a faluban az összes és csak azokat az embereket, akik nem borotválják magukat, akkor borotválja-e magát?”
A paradoxon azt látszott sugallni, hogy az egész matematika alapjaiban már nem lehet megbízni, és hogy még a matematikában sem lehet soha abszolút módon tudni az igazságot (Gödel és Turing későbbi munkássága ezt csak tovább rontotta). Russell kritikája elég volt ahhoz, hogy megingassa Frege bizalmát a logicizmus egész építményében, és ő volt olyan kegyes, hogy ezt nyíltan elismerje “Az aritmetika alaptörvényei” II. kötetének sietve írt függelékében.
De Russell főműve a monolitikus “Principia Mathematica” volt, amely három kötetben jelent meg 1910-ben, 1912-ben és 1913-ban. Az első kötet társszerzője Whitehead volt, bár a későbbi két kötet szinte teljes egészében Russell munkája. Ennek az ambiciózus műnek a törekvése nem volt más, mint kísérlet arra, hogy az egész matematikát tisztán logikai axiómákból vezesse le, elkerülve a Frege korábbi halmazelméleti munkáiban fellelhető paradoxonokat és ellentmondásokat. Russell ezt a “típusok” elméletének vagy rendszerének alkalmazásával érte el, amelyben minden matematikai egységet egy típushierarchián belüli típushoz rendelnek, így egy adott típus objektumai kizárólag a hierarchiában lejjebb lévő, előző típusok objektumaiból épülnek fel, megakadályozva ezzel a hurkokat. Minden elemhalmaz tehát más típusú, mint az egyes elemei, így nem beszélhetünk “minden halmaz halmaz halmazáról” és hasonló konstrukciókról, amelyek paradoxonokhoz vezetnek.
A “Principia” azonban a típuselmélet alapaxiómáin kívül három további axiómát is megkövetelt, amelyek puszta logikai kérdésként nem tűntek igaznak, nevezetesen a “végtelenség axiómáját” (amely garantálja legalább egy végtelen halmaz, nevezetesen az összes természetes számok halmazának létezését), a “választás axiómáját” (amely biztosítja, hogy adott “tárolók” bármely gyűjteménye, amelyek mindegyike legalább egy tárgyat tartalmaz, minden egyes tárolóból pontosan egy tárgyat lehet kiválasztani, még akkor is, ha végtelen sok tároló van, és hogy nincs “szabály” arra, hogy melyik tárgyat válasszuk ki mindegyikből) és Russell saját “redukálhatósági axiómája” (amely kimondja, hogy bármely kijelentő igazságfüggvény kifejezhető egy formálisan egyenértékű predikatív igazságfüggvénnyel).
Az alatt a mintegy tíz év alatt, amit Russell és Whitehead a “Principia”-val töltött, tervezetet tervezet után kezdtek el és hagytak el, mivel Russell folyamatosan újragondolta az alaptételeit. Russell és felesége, Alys még össze is költözött Whiteheadékkel, hogy felgyorsítsák a munkát, bár a saját házassága szenvedett, mivel Russell beleszeretett Whitehead fiatal feleségébe, Evelynbe. Végül Whitehead ragaszkodott a mű kiadásához, még akkor is, ha az nem volt (és talán soha nem is lesz) teljes, bár kénytelenek voltak saját költségükön kiadni, mivel egyetlen kereskedelmi kiadó sem akart hozzányúlni.
Principia Mathematica

A “Principia Mathematica”
A “Principia” hosszú bizonyításának egy kis része, hogy 1+1 =2
A “Principia” terjedelméről és átfogó voltáról némi képet kaphatunk abból, hogy több mint 360 oldalra van szükség annak végleges bizonyítására, hogy 1 + 1 =2.
Most széles körben úgy tartják számon, hogy Arisztotelész “Organon”-ja óta a logika egyik legfontosabb és legjelentősebb műve. Ambiciózus céljait tekintve figyelemre méltóan sikeresnek és kitartónak tűnt, és hamarosan világhírnévre tett szert Russell és Whitehead számára. Valójában csak Gödel 1931-es befejezetlenségi tétele volt az, amely végül megmutatta, hogy a “Principia” nem lehet egyszerre következetes és teljes.
Russell 1949-ben megkapta az Érdemrendet, a következő évben pedig az irodalmi Nobel-díjat. Hírneve tovább nőtt, még tudományos körökön kívül is, és későbbi életében afféle közismertté vált, bár nagyrészt filozófiai hozzájárulásainak, valamint politikai és társadalmi aktivizmusának köszönhetően, amelyet hosszú élete végéig folytatott. Szeretett Walesében halt meg influenzában, 97 éves korában.
| << Vissza Hardyhoz és Ramanujanhoz | Előre Hilberthez >> |