Chemguide: Support for CIE A level Chemistry
Learning outcome 11.2(f)
This statement is about partition coefficents.
Before you go on, you should find and read the statement in your copy of the syllabus.
megoszlási
Ha van két nem keverhető folyadék, például éter és víz, és felrázzuk őket egy elválasztótölcsérben, akkor nyilvánvalóan két réteget képeznek. Az éter kisebb sűrűségű, mint a víz, ezért alkotja a felső réteget.
Tegyük fel most, hogy felrázunk egy éter és víz keveréket, amely olyan anyagot tartalmaz, amely mindkettőben oldódik. Tegyük fel, hogy az anyag, X, jobban oldódik az éterben, mint a vízben.
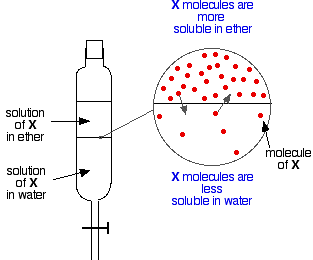
Az X részecskéi átlépik a két folyadékréteg közötti határvonalat, és hamarosan beáll a dinamikus egyensúly. Minden egyes részecske, amely a felső rétegbe kerül, egy részecske visszamegy az alsó rétegbe.
Egy egyenletet írhatnál erre:
. . és mint minden más egyensúlyi állapotra, erre is találhatunk egy egyensúlyi állandót:
Ezt az egyensúlyi állandót megoszlási együtthatónak nevezzük, és gyakran a Kpc jelet kapja.
A többi egyensúlyi állandóhoz hasonlóan a megoszlási együttható is állandó hőmérsékleten állandó, de van néhány más megkötés is. Csak meglehetősen híg oldatok esetén működnek megfelelően, és az oldott anyagnak mindkét oldószerben azonos kémiai formában kell lennie. Nem léphet reakcióba, nem ionizálódhat vagy társulhat (például dimerekké egyesülhet).
A megoszlási együttható számítása
Egy megjegyzés a mértékegységekről
Megjegyezzük, hogy a megoszlási együttható két koncentráció egyszerű hányadosa. Nem számít, hogy milyen koncentrációs mértékegységet használsz – amíg ugyanazt használod fent és lent.
Felhasználhatod a mol dm-3 mértékegységet, de gyakrabban használod a g cm-3 – gramm per köbcentiméter.
Technikailag a szögletes zárójel csak a mol dm-3 koncentrációra használható, de az Application Support Booklet és a CIE jelölési sémái egyaránt használják más mértékegységekre is.
Nem vagyok hajlandó erre, ezért inkább az “X koncentrációja” kifejezést fogom használni, mint ahol nem szabványos koncentrációs egységeket használunk.
megoszlási együttható számítása
Mikor 1,00 g X 100 cm3 vízben lévő oldatát 10 cm3 éterrel rázzuk össze, 0,80 g X került az éterrétegbe. Számítsa ki X megoszlási együtthatóját az éter és a víz között.
Ha két oldószer közötti megoszlási együttható kiszámítására kérik, akkor az elsőként említett oldószer koncentrációja kerül a Kpc kifejezés tetejére. Tehát ebben az esetben:
Elégséges információval rendelkezel ahhoz, hogy mindkét koncentrációt g cm-3-ban számítsd ki.
X koncentrációja az éterben = 0,80/10 g cm-3
Ha 0,80 g került az éterbe, akkor 1,00 – 0,80 g = 0.20 g maradt a vízben.
X koncentrációja a vízben = 0,20/100 g cm-3
Szóval:
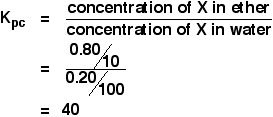
Az éterben és a vízben lévő koncentrációkat nyilvánvalóan tényleges számokként is kiszámíthatnád, mielőtt beírnád a kifejezésbe. Csináld úgy, ahogy neked a legkényelmesebb.
Az ilyen megoszlási együtthatóknak nincsenek egységei – az egységek kioltják egymást, mert felül és alul ugyanazok.
A megoszlási együtthatókkal kapcsolatos számítások
A CIE tanterv kifejezetten azt mondja, hogy meg kell tudnod számolni a megoszlási együtthatót (más szóval, amit most csináltunk). Egyáltalán nem mond semmit arról, hogy más dolgok kiszámításához használjuk őket. Ezeket az extra számításokat az Alkalmazástámogató füzet tárgyalja, és 2013 júniusáig kétszer kérdezték őket a vizsgákon (mindkétszer 2009-ben).
A Coursebook nem tartalmazza őket (nagyon helyesen!), mert a tanterv nem említi őket, és ezt a könyvet a CIE vizsgáztatói a tananyag “teljes és pontos lefedettségeként” jóváhagyták. Ez tehát azt jelenti, hogy a CIE a jövőben nem fog több kérdést feltenni? Ne számítson rá!”
Egy alapvető példa
Azt az esetet fogjuk használni, mint korábban – ugyanazok az oldószerek, ugyanaz az X és ugyanaz a megoszlási együttható, amit az imént kiszámítottunk.
Ezúttal azt fogjuk kiszámítani, hogy mennyi extrahálódott volna az éterrétegbe, ha az eredeti 1,00 g X-et 100 cm3 vízben tartalmazó oldatot csak 5 cm3 éterrel rázzuk fel.
A kivont X tömegét próbáljuk kiszámítani. Nevezzük ezt m-nek.
Most dolgozzunk ki egy kifejezést az X éterben lévő oldatának koncentrációjára.
X koncentrációja éterben = m/5 g cm-3
Mi a helyzet a vízzel? A vízben (1,00 – m) g X marad. Tehát:
az X koncentrációja a vízben = (1,00 – m)/100 g cm-3
Most mindezt beilleszthetjük a megoszlási együttható kifejezésbe. Ne feledjük, hogy az X megoszlási együtthatóját az éter és a víz között már kiszámoltuk 40-ben.
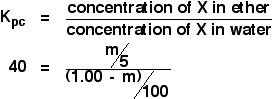
Ezután már csak egy egyszerű, de kissé fárasztó algebrai művelettel állunk szemben:
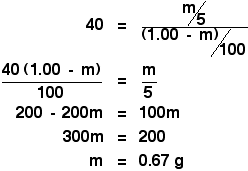
Még fárasztóbb!
A megoszlási együttható megtalálására végzett eredeti számításban azt mondtuk, hogy ha az eredeti, 100 cm3 vízben lévő 1,00 g X oldatot 10 cm3 éterrel rázzuk fel, akkor 0,80 g X-et vonunk ki.
Azt 5 cm3 éterrel felrázva most kiszámoltuk, hogy 0,67 g X-et vonunk ki.
Ezzel 0,33 g X maradna a 100 cm3 vízben. Tegyük fel, hogy ezt az oldatot gondosan megtartottuk, majd egy második friss 5 cm3 éterrel felrázzuk.
Mennyit vonnánk ki összesen X-ből, ha az étert két külön 5 cm3-es tételben használnánk a 10 cm3 helyett egy menetben?
A második adag éterrel kivont X tömegét nevezzük n-nek – hogy ne keveredjünk össze.
Munkáljunk ki egy kifejezést az X éterben lévő oldat koncentrációjára.
X koncentrációja éterben = n/5 g cm-3
Mi lesz a vízzel? A második extrakció után (0,33 – n) g X marad a vízben. Tehát:
Az X koncentrációja a vízben = (0,33 – n)/100 g cm-3
Most mindezt beilleszthetjük az éter és a víz közötti X megoszlási együttható kifejezésbe, mint korábban.
Ez azt jelenti, hogy ha a két 5 cm3 -es adag étert egyesítenénk, akkor összesen 0,67 + 0,22 g X-et vonnánk ki, ami 0.89 g.
Eredetileg azt mondták, hogy ha ezt csak egyszer csináltad volna, egyetlen 10 cm3 -es tételben az éterrel, akkor csak 0,80 g-ot extraháltál volna.
Egy hatékonyabb extrakciót kapsz, ha az oldószert a fentiek szerint kisebb térfogatokra osztod.
Egy ilyen technikát használsz egyes szerves vegyületek előállítása során. Kivonod azt, amit elő akarsz állítani valamilyen zavaros oldatból vízben úgy, hogy az egy szerves oldószerbe kerüljön. Ezután óvatos desztillációval eltávolítod az oldószert.
A CIE 2009. júniusi 4. dolgozatának 8. kérdésében ehhez hasonló kérdést tett fel. Ki kellett számolni egy értéket a megoszlási együtthatóra, majd azt egy kétlépéses extrakcióban pontosan a fentiek szerint felhasználni. A számítás 4 pontot ért. Ez lehet, hogy fárasztó, és (a megoszlási együttható kiszámításától eltekintve) nem szerepel a tananyagban, de nem engedheti meg magának, hogy ne tudja megcsinálni.
