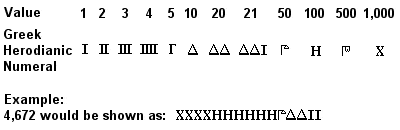
Ősi görög heródesi számok
Amint a görög birodalom kezdte kiterjeszteni befolyási övezetét Kis-Ázsiára, Mezopotámiába és azon túlra, a görögök elég okosak voltak ahhoz, hogy hasznos elemeket vegyenek át és adaptáljanak az általuk meghódított társadalmakból. Ez a matematikájukra éppúgy igaz volt, mint bármi másra, és mind a babilóniaiaktól, mind az egyiptomiaktól átvettek matematikai elemeket. De hamarosan saját jogon is fontos hozzájárulásokat kezdtek tenni, és most először ismerhetjük el az egyének hozzájárulásait. A hellenisztikus korszakra a görögök minden idők egyik legdrámaibb és legfontosabb forradalmát vezették a matematikai gondolkodásban.
Az attikai vagy heródesi számrendszer
Az attikai vagy heródesi számrendszer néven ismert ókori görög számrendszer i. e. 450 körül volt teljesen kidolgozva, és valószínűleg már az i. e. 7. században rendszeresen használták. Ez a korábbi egyiptomi rendszerhez (és még inkább a későbbi római rendszerhez) hasonló 10-es bázisú rendszer volt, amelyben az 1, 5, 10, 50, 100, 500 és 1000 szimbólumok annyiszor ismétlődtek, ahányszor a kívánt szám ábrázolásához szükséges volt. Az összeadás az összeadandó számok szimbólumainak (1-es, 10-es, 100-as stb.) külön-külön történő összeadásával történt, a szorzás pedig fáradságos, egymást követő megduplázásokon alapuló folyamat volt (az osztás ennek a folyamatnak a fordítottján alapult).
Thalész metszéspont-tétele
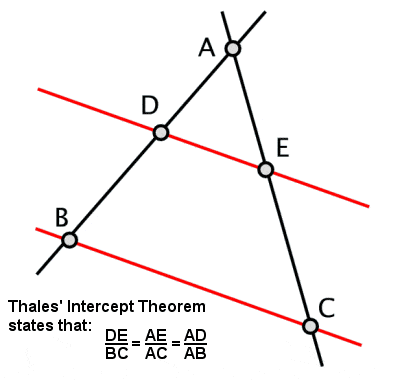
Thalész metszéspont-tétele
A görög matematika nagy része azonban a geometrián alapult. Thalészt, az ókori Görögország hét bölcsének egyikét, aki az i. e. 6. század első felében élt a kis-ázsiai Jón-tenger partvidékén, általában úgy tartják, hogy ő volt az első, aki lefektette a geometria absztrakt fejlődésének irányelveit, bár amit a munkásságáról (például a hasonló és derékszögű háromszögekről) tudunk, ma már eléggé elemi erejűnek tűnik.
Thalész felállította a Thalész-tétel néven ismertté vált tételt, miszerint ha egy háromszöget úgy rajzolunk egy körön belül, hogy a hosszú oldala a kör átmérője, akkor a szemben lévő szög mindig derékszög lesz (valamint néhány más, ebből levezetett kapcsolódó tulajdonságot is). Neki tulajdonítanak egy másik tételt is, amelyet szintén Thalész-tételnek vagy metszéspont-tételnek neveznek, és amely azoknak az egyenes szakaszoknak az arányairól szól, amelyek akkor keletkeznek, ha két egymást metsző egyenest egy párhuzamos pár metszi (és ennek folytán a hasonló háromszögek oldalainak arányairól).
Az i. e. 6. századi szamoszi matematikus, Püthagorasz legendája azonban bizonyos mértékig a görög matematika születésének szinonimájává vált. Valójában úgy tartják, hogy ő alkotta meg mind a “filozófia” (“a bölcsesség szeretete”), mind a “matematika” (“az, ami tanult”) szavakat. Püthagorasz volt talán az első, aki felismerte, hogy meg lehet alkotni egy teljes matematikai rendszert, amelyben a geometriai elemek megfeleltek a számoknak. Pitagorasz tétele (vagy a Pitagorasz-tétel) az egyik legismertebb matematikai tétel. De, mint látni fogjuk, továbbra is ellentmondásos alak maradt, és a görög matematika korántsem korlátozódott egyetlen emberre.
Három geometriai probléma
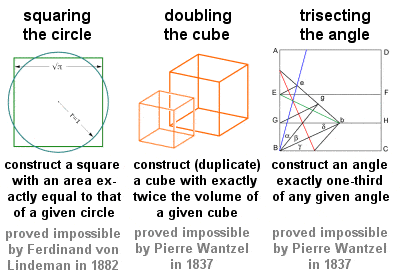
A három klasszikus probléma
A görög geometria korai korszakára nyúlik vissza különösen három geometriai probléma, amelyeket gyakran a három klasszikus problémának neveznek, és amelyeket mind tisztán geometriai módszerekkel, csupán egy egyenes vonalzó és egy iránytű segítségével kell megoldani: “a kör négyszögesítése (vagy kvadratúrája)”, “a kocka megduplázása (vagy megkettőzése)” és “egy szög háromszögezése”. Ezek az áthidalhatatlan problémák nagy hatással voltak a későbbi geometriára, és számos gyümölcsöző felfedezéshez vezettek, bár tényleges megoldásaikra (vagy, mint kiderült, lehetetlenségük bizonyítására) egészen a 19. századig kellett várni.”
Hippokratész Khioszból (nem összetévesztendő a nagy görög orvossal, Hippokratész Kószból. Részletes életrajz itt.) volt az egyik ilyen görög matematikus, aki a Kr. e. 5. században ezekkel a problémákkal foglalkozott (a “kör négyszögesítése” problémához való hozzájárulása Hippokratész Lúnája néven ismert). Az ő nagy hatású, i. e. 440 körül keletkezett “Elemek” című könyve volt a geometria elemeinek első gyűjteménye, és műve fontos forrása volt Euklidész későbbi munkáinak.
Zenó Akhilleusz és a teknősbéka paradoxona
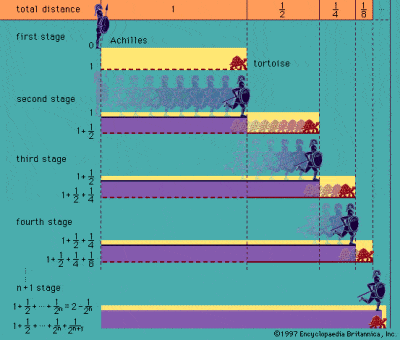
Zenó Akhilleusz és a teknősbéka paradoxona
A görögök voltak azok, akik először foglalkoztak a végtelenség gondolatával, ahogyan azt a Kr. e. 5. században az elei Zénón filozófusnak tulajdonított közismert paradoxonok leírják. Paradoxonjai közül a leghíresebb az Akhilleusz és a teknősbéka paradoxona, amely egy elméleti versenyt ír le Akhilleusz és egy teknősbéka között. Akhilleusz előnyt ad a sokkal lassabb teknősnek, de mire Akhilleusz eléri a teknős kiindulópontját, a teknős már előrébb jár. Mire Akhilleusz odaér, a teknős már megint továbbhaladt, stb. stb., így a gyors Akhilleusz elvileg soha nem érheti utol a lassú teknőst.
Az ehhez hasonló paradoxonok és Zénón úgynevezett dichotómia-paradoxona a tér és az idő végtelen oszthatóságán alapulnak, és azon a gondolaton alapulnak, hogy egy fél plusz egy negyed plusz egy nyolcad plusz egy tizenhatod, stb. stb. a végtelenségig soha nem lesz teljesen egy egész. A paradoxon azonban abból a téves feltételezésből ered, hogy véges idő alatt nem lehet végtelen számú diszkrét kötőjelet kitölteni, bár a tévedés végleges bizonyítása rendkívül nehéz. Az ókori görög Arisztotelész volt az első a sok közül, aki megpróbálta megcáfolni a paradoxonokat, különösen azért, mert szilárdan hitt abban, hogy a végtelen mindig csak potenciális lehet, nem pedig valóságos.
Demokritosz, aki leginkább arról az előrelátó elképzeléséről híres, hogy minden anyag apró atomokból áll, szintén a matematika és a geometria úttörője volt az i. e. 5. – 4. században, és olyan címekkel ellátott műveket készített, mint “A számokról”, “A geometriáról”, “A tangenciákról”, “A leképezésről” és “Az irracionálisokról”, bár ezek a művek nem maradtak fenn. Azt tudjuk, hogy az elsők között volt, aki megfigyelte, hogy egy kúp (vagy piramis) térfogata egyharmada az azonos alapterületű és magasságú henger (vagy prizma) térfogatának, és talán ő az első, aki komolyan foglalkozott a tárgyak végtelen számú keresztmetszetre való felosztásával.
Mindamellett kétségtelenül igaz, hogy különösen Püthagorasz nagy hatással volt az utána következőkre, köztük Platónra, aki Kr. e. 387-ben megalapította híres athéni akadémiáját, és pártfogoltjára, Arisztotelészre, akinek a logikáról szóló munkáját több mint kétezer éven át tekintették meghatározónak. A matematikus Platónt leginkább az öt platóni szilárd test leírásáról ismerik, de a matematika tanítójaként és népszerűsítőjeként végzett munkásságának értékét nem lehet eléggé hangsúlyozni.
Platón tanítványának, a knidosi Eudoxosznak tulajdonítják általában a (később Arkhimédész által kifejlesztett) “kimerítési módszer” első megvalósítását, az egymást követő közelítésekkel történő integrálás korai módszerét, amelyet a piramis és a kúp térfogatának kiszámításához használt. Az arányosság általános elméletét is kidolgozta, amely alkalmazható volt a két egész szám hányadosaként ki nem fejezhető inkommensurábilis (irracionális) nagyságokra, valamint a commensurábilis (racionális) nagyságokra is, kiterjesztve ezzel Püthagorasz hiányos elképzeléseit.
A görögök talán legfontosabb egyedi hozzájárulása azonban – és Püthagorasz, Platón és Arisztotelész mind hatással volt rájuk e tekintetben – a bizonyítás gondolata volt, és a deduktív módszer, amely logikai lépések segítségével a kezdetben feltételezett axiómákból kiindulva bizonyítja vagy cáfolja a tételeket. A régebbi kultúrák, mint például az egyiptomiak és a babilóniaiak, az induktív gondolkodásra támaszkodtak, vagyis arra, hogy ismételt megfigyelések segítségével állítsák fel az ökölszabályokat. A bizonyításnak ez a koncepciója adja a matematika erejét, és biztosítja, hogy a bizonyított elméletek ma is ugyanolyan igazak legyenek, mint kétezer évvel ezelőtt, és amely megalapozta Euklidész és az utána következők szisztematikus matematikai megközelítését.
| << Vissza az egyiptomi matematikához | Előre Püthagoraszhoz >> |