Mi a rács?
A rács a kristályt alkotó részecskék elrendeződését leíró pontok rendezett sorozata.
A kristály egységcelláját a rácspontok határozzák meg.Az egységcella a kristály legkisebb része, amely a három dimenzióban történő elmozdulással szabályosan megismételve létrehozza az egész kristályt.
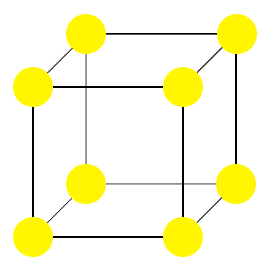
Az itt látható képen például egy primitív köbös szerkezet egységcellája látható.
A rajzolt szerkezetben az összes részecske (sárga) azonos.Ebben a konkrét esetben az egységcellát meghatározó rácspontok egybeesnek a kristály részecskéinek középpontjaival. Ennek nem kell mindig így lennie.
Az ionrács
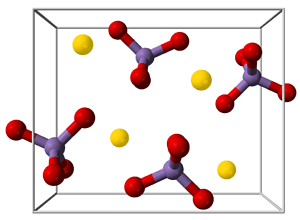
Ha egy kristály ionokból áll, akkor a vegyületet ionrácsként írhatjuk le.
Az ionrácsok jól ismert példái a nátrium-klorid, a kálium-permanganát, a bórax (nátrium-borát) és a réz(II)szulfát.

A kovalens rács
Ha egy kristály kovalens kötésű atomokból áll, akkor kovalens rácsnak vagy végtelen kovalens rácsnak nevezhető.
A kovalens rácsok jól ismert példái a gyémánt, a kvarc (szilícium-dioxid), a szilícium és a szürke ón.
Rácsállandók
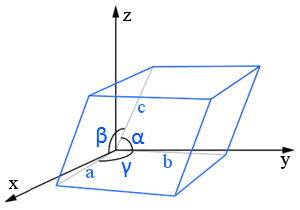
A rácsállandók (vagy rácsparaméterek) az egységcella élei közötti hosszúságok és szögek.
Ebben a paralelepipedikus rácsdiagramban a rácsállandók a, b és c (hosszúságok) és α, β és γ (szögek).
Rácsszerkezetek
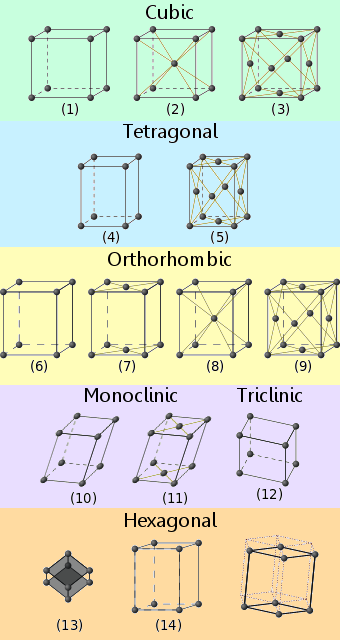
A kristályos anyagok tizennégy elismert rácselrendezés valamelyikébe illeszkednek.Ezeket Bravais-rácsoknak nevezik.
A kristályrácsrendszerek nevei, az ábrákon szereplő számoknak megfelelően, a következők:
1. Primitív köbös
2. Testközéppontos köbös
3. Arcközéppontos köbös
4. Primitív tetragonális
5. Testközéppontú tetragonális
6. Primitív orthorombikus
7. Alapközéppontú orthorombikus
8. Testközéppontú orthorombikus
9. Arcközpontú orthorombikus
10. Primitív monoklin
11. Bázisközpontú monoklin
12. Triklin
13. Romboéder
14. Hexagonális
Rácshibák
Ha egy kristályról feltételeznénk, hogy matematikailag tökéletes ionrácson alapul, akkor a számított szakítószilárdsága sokkal nagyobb lenne a ténylegesen megfigyeltnél
.