Talking in Three Dimensions

Nézd meg ezt a képet egy négyszögletes prizmáról:

Hány csúcsa van? 8

Hány éle van? 12

Hány oldala van? 6

Egyszerű, igaz?

Próbáljunk meg egy másikat. Nézzük meg ezt a képet egy kúpról:

Hány csúcsa van? A csúcson lévő pont számít?

Hány éle van? Hmm, nem vagyok benne biztos. Az éleknek nem egyenesnek kellene lenniük?

Hány oldala van? Ez könnyű! Egy. Van egy kör alakú felület az alján. De az nem sokszög, szóval akkor is egy arc? Ja, és hogy hívjam a kúp másik felületét? Az oldalaknak nem laposnak kell lenniük?

Az 1., 2. és 3. osztályos tanároktól gyakran kapunk kérdéseket azzal kapcsolatban, hogyan kell leírni bizonyos háromdimenziós testek, különösen a hengerek és a kúpok tulajdonságait. A TEKS szerint a tanulóknak a háromdimenziós testeket olyan formális geometriai kifejezésekkel kell leírniuk, mint a csúcs, él és felület. A probléma az, hogy olyan nyelvet próbálunk használni, amely az alakzatok egy osztálya esetében működik, hogy egy teljesen más osztály tulajdonságait írjuk le.

A háromdimenziós alakzatok, például a prizmák és a piramisok poliéderek. “A geometriában a poliéder egyszerűen egy háromdimenziós szilárd test, amely sokszögek gyűjteményéből áll, amelyek általában az éleiknél kapcsolódnak össze.” (Forrás) Ezeknek a szilárd testeknek “lapos sokszögfelületeik, egyenes éleik és közös sarkaik vagy csúcsaik vannak”. (Forrás)

A gömbök, hengerek és kúpok viszont nem poliéderek. Ennek következtében nem használhatjuk pontosan ugyanazt a nyelvet a leírásukra, vagy ha mégis ugyanazt a nyelvet használjuk, akkor azzal a megjegyzéssel, hogy a definíciók nem azonosak. Vegyük például a csúcs szót.

Egy négyszögletes prizmán a csúcs az az éles pont vagy sarok, ahol az élek találkoznak. Egy téglalap alakú prizmának 8 csúcsa van.

Ez a kifejezés azonban egy kúp csúcsának leírására is használható. Ugyanaz a kifejezés, de nem ugyanaz a definíció. Ahogy Dr. Math mondja,

Az igazán trükkös rész itt az, hogy a kúp “csúcsának” semmi köze az élekhez, ezért egy teljesen új definícióra van szükség; és nem tudok egy igazán jó elemi szintű definíciót találni arra, amit nyilvánvalóan arra gondolnak, ami egyszerűen egy “pont.”

Amint a diákok haladóbb matematikát folytatnak, kifinomultabb nyelvezetet és definíciókat tudnak kidolgozni. Addig is, amíg az általános iskolában vannak, az RRISD-ben a kúp csúcsa kifejezést használjuk a kúp ezen tulajdonságának leírására.

Ha azt akarjuk, hogy a tanulók leírják és osztályozzák ezt a fajta háromdimenziós szilárd testet, akkor ehhez hozzáférhető nyelvezetet kell biztosítanunk.

Mi a helyzet a kúp többi tulajdonságával? Ismét az a célunk, hogy olyan nyelvezetet biztosítsunk, amely az általános iskolai tanulók számára hozzáférhető és leíró jellegű ezekkel a tulajdonságokkal kapcsolatban, felismerve, hogy tanulóink az iskolai pályafutásuk során később formálisabb megértést fognak kialakítani. A kúp leírására azt mondanánk, hogy a kúpnak van egy kör alakú alapja, vagyis az a sík felület, amelyen a kúp nyugszik. Azt is mondjuk, hogy van egy görbe pereme az alap mentén, és egy görbe felülete, amely ettől a peremtől egészen a csúcsáig tart.

Mi a helyzet a hengerrel? Most, hogy már rendelkezünk hozzáférhető nyelvvel a kúp tulajdonságainak leírására, ezt a nyelvet kiterjeszthetjük a hengerek tulajdonságainak leírására.

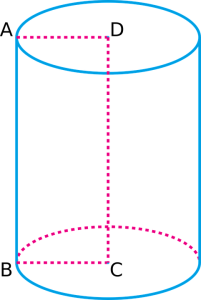
A fenti henger két kör alakú alapból áll, egy a tetején és egy az alján. Két görbe éle is van, egy a tetején és egy az alján. Végül van egy görbe felülete, amely az alsó éltől a felső élig terjed.

Hozzá kell tennem, hogy mind az általam leírt kúp, mind a henger derékszögű körkúp és derékszögű henger. A sokszögekhez és a poliéderekhez hasonlóan ezekre az alakzatokra is sok másfajta példa létezik. Például a kúp vagy a henger lehet ferde, tehát ferde.

A tanulók számára fontos, hogy sokféle példát lássanak a két- és háromdimenziós alakzatokra. Minél többel találkoznak, annál többet kell szembesülniük a definíciókkal és a terminológiával, ami azt szolgálja, hogy megerősödjön bennük a tulajdonságok megértése, és az, hogy ezek hogyan segítenek azonosítani és osztályozni ezeket az alakzatokat.

Hogyan néz ez ki a STAAR-on?

A 2016-ban megjelent tesztben a STAAR egy olyan kérdést tett fel, amely éppen erre a témára vonatkozott, és megerősítette az RRISD-ben használt szókincset.

A helyes válasz: F Nincs csúcsuk. Ha megnézzük a B halmazt, észrevehetjük, hogy tartalmaz egy kúpot, amelynek, mint korábban már megbeszéltük, van egy csúcsa. Ha a Texasi Oktatási Hivatal nem használná a kúp csúcspontja kifejezést, akkor valószínűleg az A halmazban is látnánk a kúpot.

Itt egy búcsúgondolat Dr. Math-től:

Az, hogy milyen definíciót használunk, attól függ, hogy mit fogunk vele kezdeni. Ha csak tárgyakat írsz le, akkor az én laza definícióm is megfelel. Ha síkokkal és szögekkel kapcsolatos tételeket akarsz bizonyítani, akkor a sokszög definícióra kell szorítkoznod, de akkor nem fogsz kúpokra vonatkozó kérdéseket feltenni. Azt hiszem, az emberek gyakran nem veszik észre, hogy bár a matematikában sajátos definíciókat használunk, ezek a definíciók területről területre változnak, mivel egy bizonyos kontextushoz igazodnak. Én is ezt próbálom itt elérni.