16.3 Vegyes stratégiák
Tanulási cél
- Mely játékok igénylik vagy megengedik a randomizálást a megoldásuk részeként?
Mondjuk meg újra a filléres játékot, amit a 16. ábra szemléltet.13 “Matching pennies again”.
16.13. ábra Matching pennies again
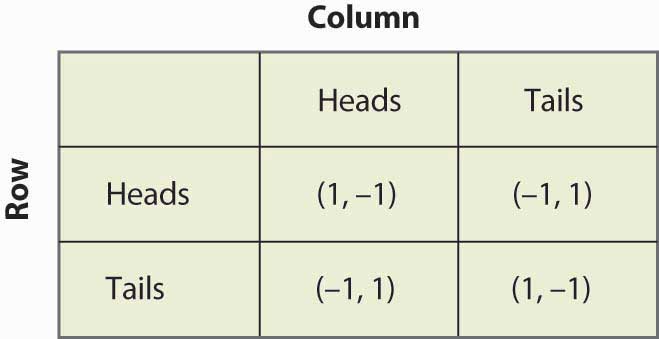
Tegyük fel, hogy Row úgy véli, hogy az oszlop p valószínűséggel fejet játszik. Akkor ha Row fejet játszik, Row p valószínűséggel 1-et kap, és -1-et (1 – p) valószínűséggel, ami 2p – 1 várható értéket jelent. Hasonlóképpen, ha Row írásjelet játszik, Row -1-et kap p valószínűséggel (ha az oszlop fejet játszik), és 1-et (1 – p) valószínűséggel, ami 1 – 2p várható értéket jelent. Ezt foglalja össze a 16.14. ábra “Vegyes stratégia fillérek párosításában”.
Ha 2p – 1 > 1 – 2p, akkor Row átlagosan jobban jár, ha fejet játszik, mint ha írásost. Hasonlóképpen, ha 2p – 1 < 1 – 2p, akkor Row jobban jár, ha Írással játszik, mint Fejjel. Ha viszont 2p – 1 = 1 – 2p, akkor Row ugyanazt a nyereséget kapja, függetlenül attól, hogy Row mit tesz. Ebben az esetben Row játszhat fejet, játszhat írást, vagy feldobhat egy érmét és randomizálhatja Row játékát.
Egy vegyes stratégiájú Nash-egyensúlyEgy olyan Nash-egyensúly, amelyben legalább egy játékos randomizált stratégiát játszik, és egyetlen játékos sem tudja növelni a várható nyereményét alternatív stratégia játszásával. magában foglalja, hogy legalább egy játékos randomizált stratégiát játszik, és egyetlen játékos sem tudja növelni a várható nyereményét alternatív stratégia játszásával. Az olyan Nash-egyensúlyt, amelyben egyetlen játékos sem randomizál, tiszta stratégiájú Nash-egyensúlynak nevezzükA Nash-egyensúlyt, amelyben egyetlen játékos sem randomizál..
16.14. ábra Vegyes stratégia a fillérek párosításában
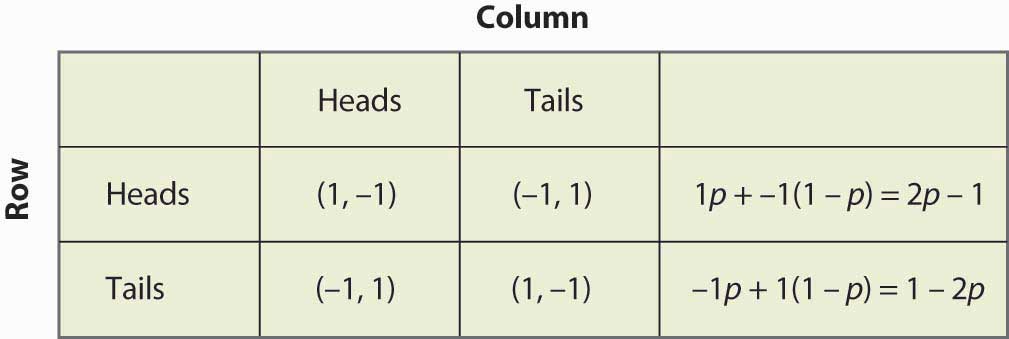
Megjegyezzük, hogy a randomizáláshoz a várható kifizetések egyenlősége szükséges. Ha egy játékosnak az A vagy a B stratégiára kell randomizálnia, akkor mindkét stratégiának ugyanazt a várható kifizetést kell eredményeznie. Ellenkező esetben a játékos az egyiket előnyben részesítené, és nem játszaná a másikat.
A vegyes stratégia kiszámításának van egy olyan eleme, amely gyakran zavarónak tűnik. Tegyük fel, hogy Row randomizálni fog. Akkor Row kifizetéseinek egyenlőnek kell lennie minden olyan stratégia esetén, amelyet Row pozitív valószínűséggel játszik. De a Row kifizetéseinek egyenlősége nem határozza meg azokat a valószínűségeket, amelyekkel Row a különböző sorokat játssza. Ehelyett a sor kifizetéseinek egyenlősége határozza meg azokat a valószínűségeket, amelyekkel az oszlop a különböző oszlopokat játssza. Ennek az az oka, hogy az oszlop valószínűségei határozzák meg a sor várható nyereményeit; ha sor véletlenszerűen játszik, akkor az oszlop valószínűségeinek olyannak kell lenniük, hogy sor hajlandó legyen véletlenszerűen játszani.
Így például kiszámítottuk a sor számára a fejes játék nyereményét, ami 2p – 1, ahol p annak a valószínűsége, hogy az oszlop fejet játszik. Hasonlóképpen, a Sor számára az Írás játék kifizetése 1 – 2p volt. Row akkor hajlandó randomizálni, ha ezek egyenlőek, ami p = ½-re oldódik meg.
Most próbáljunk meg egy valamivel nagyobb kihívást jelentő példát, és nézzük meg újra a nemek harcát. A 16.15. ábra “Vegyes stratégia a nemek csatájában” ismét a kifizetéseket szemlélteti.
16.15. ábra Vegyes stratégia a nemek csatájában
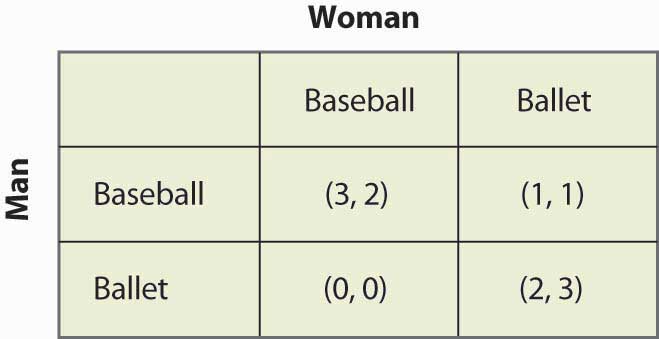
Ez a játék két tiszta stratégiájú Nash-egyensúlyt tartalmaz: (Baseball, baseball) és (Balett, balett). Létezik vegyes stratégia? A vegyes stratégia kiszámításához a Nő menjen a Baseball játékba p valószínűséggel, a Férfi pedig a Baseball játékba q valószínűséggel. 16.16. ábra “A vegyes stratégia teljes számítása” tartalmazza a vegyes stratégia kifizetéseinek kiszámítását minden játékos számára.
16. ábra.16 A vegyes stratégia teljes számítása
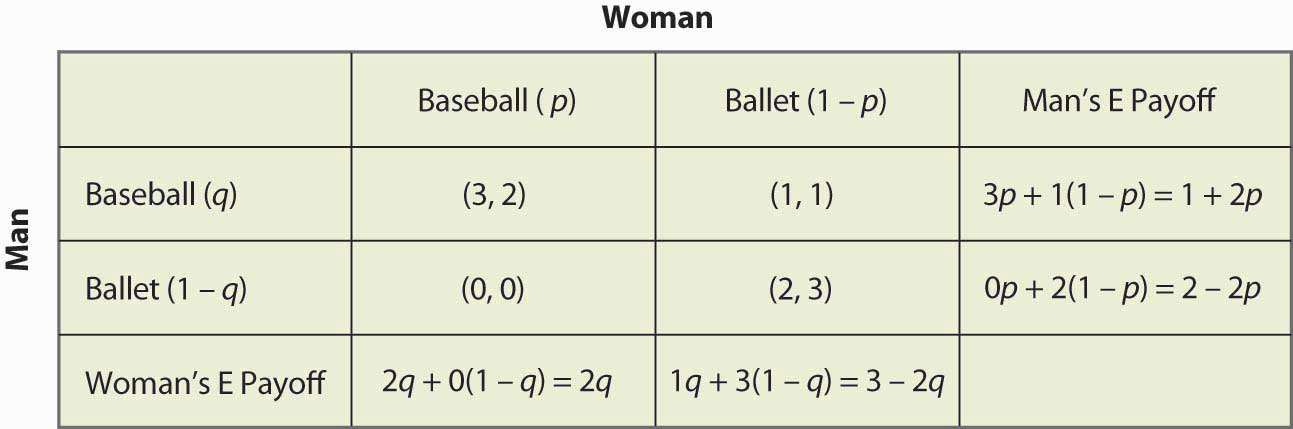
Ha például a Férfi (soros játékos) a Baseball-meccsre megy, akkor 3-at kap, ha a Nő a Baseball-meccsre megy (p valószínűséggel), egyébként pedig 1-et kap, a várható kifizetés 3p + 1(1 – p) = 1 + 2p. A többi számítás hasonló, de mindenképpen végig kell futni a logikán és ellenőrizni minden egyes számítást.
A vegyes stratégia a nemek harca játékban mindkét félnek randomizálnia kell (mivel bármelyik fél tiszta stratégiája megakadályozza a másik fél randomizálását). A Férfi közömbössége a baseball-játékba és a bálba való belépés között 1 + 2p = 2 – 2p-t igényel, ami p = ¼-et eredményez. Vagyis a férfi hajlandó véletlenszerűen eldönteni, hogy melyik eseményre megy el, ha a nő az esetek ¾-ében a balettre megy, egyébként pedig a baseballmeccsre. Ezáltal a Férfi közömbössé válik a két esemény között, mert szívesebben van a Nővel, de a Baseball-meccsen is szívesen van. Ahhoz, hogy kiegyenlítse azt az előnyt, amit a játék jelent számára, a Nőnek gyakrabban kell a Balettben lennie.
Hasonlóképpen, ahhoz, hogy a Nő randomizáljon, a Nőnek egyenlő kifizetéseket kell kapnia a Baseball-meccsre és a Balettre járásból, amihez 2q = 3 – 2q, vagy q = ¾ szükséges. Így annak valószínűsége, hogy a Férfi elmegy a baseball-meccsre, ¾, és ¼-szer megy a balettre. Ezek független valószínűségek, így annak a valószínűségnek a kiszámításához, hogy mindketten elmennek a baseballmeccsre, megszorozzuk a valószínűségeket, ami 3/16-ot eredményez. A 16.17. ábra “Vegyes stratégia valószínűségei” kitölti mind a négy lehetséges kimenetel valószínűségeit.
16.17. ábra Vegyes stratégia valószínűségei
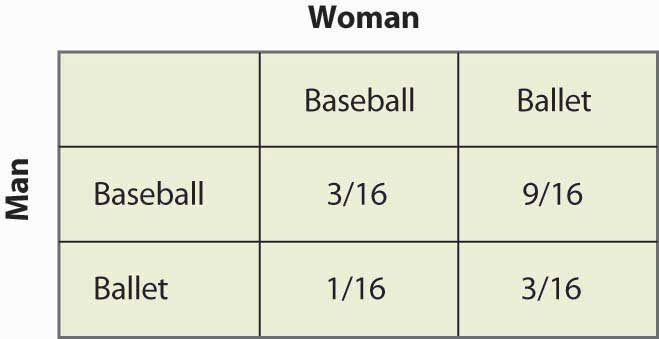
Megjegyezzük, hogy az esetek több mint felében (Baseball, Balett) a vegyes stratégia eredménye, és a két ember nincs együtt. Ez a koordináció hiánya általában a vegyes stratégiájú egyensúlyok jellemzője. A két játékos várható nyereménye is könnyen kiszámítható. Az Ember nyereménye 1 + 2p = 2 – 2p, és mivel p = ¼, az Ember 1½-et kap. Egy hasonló számítás azt mutatja, hogy a nő nyereménye ugyanez. Tehát mindketten rosszabbul teljesítenek, mintha a kevésbé preferált kimenetelű koordinációjukat végeznék. De ez a vegyes stratégiájú Nash-egyensúly, bármennyire is nem kívánatosnak tűnik, abban az értelemben Nash-egyensúly, hogy a másik fél viselkedése miatt egyik fél sem tudja javítani a saját kifizetését.
A nemek harcában a vegyes stratégiájú Nash-egyensúly valószínűtlennek tűnhet; és elvárhatnánk, hogy a pár hatékonyabban koordináljon. Valóban, egy egyszerű telefonhívásnak ki kellene zárnia a vegyes stratégiát. Nézzünk tehát egy másik, a nemek harcához kapcsolódó játékot, ahol a koordináció kudarcának több értelme van. Ez a “csirkejáték”. Ebben a játékban két játékos hajt egymás felé, megpróbálva meggyőzni a másikat, hogy térjen ki, és végül egy árokba kanyarodjon. Ha mindketten az árokba kanyarodnak, akkor az eredményt döntetlennek nevezzük, és mindketten nullát kapnak. Ha az egyik kitér, a másik pedig nem, akkor a kitérő sofőr veszít, a másik sofőr pedig nyer, és a győztesnek adunk egy pontot.Vegyük észre, hogy ha egy játékos nyereményéhez konstansot adunk, vagy a játékos nyereményét megszorozzuk egy pozitív konstanssal, az nem befolyásolja a Nash-egyensúlyt – sem a tiszta, sem a vegyes egyensúlyt. Ezért mindig hagyhatjuk, hogy minden játékos egyik kimenetele nulla legyen, a másik pedig egy. Az egyetlen fennmaradó kérdés az, hogy mi történik, ha egyik sem adódik, amely esetben összeomlás következik be. Ebben a változatban a nyereményt a kitérés veszteségének négyszeresére állítottuk be, ahogy a 16.18. ábra “Csirke” mutatja, de megváltoztathatjuk a játékot, és megnézhetjük, mi történik.
16.18. ábra Csirke
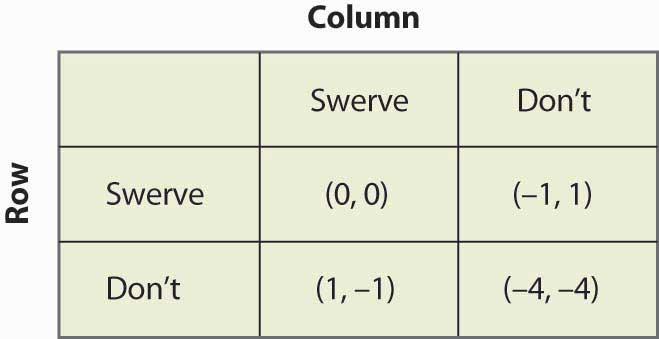
Ez a játék két tiszta stratégiájú egyensúlyi helyzetet tartalmaz: (Kitérés, nem) és (Nem, kitérés). Ezen kívül van egy vegyes stratégiája is. Tegyük fel, hogy az oszlop p valószínűséggel kitér. Ekkor a sor 0p + -1(1 – p) kap a kitérésből, 1p + (-4)(1 – p) a nem kitérésből, és a sor akkor véletlenszerű, ha ezek egyenlőek, amihez p = ¾ szükséges. Vagyis annak valószínűsége, hogy az oszlop kitér a vegyes stratégiájú egyensúlyban ¾. Ellenőrizhetjük, hogy a soros játékosnak ugyanez a valószínűsége, ha a soros kitérésének valószínűségét q-val egyenlővé tesszük, és kiszámítjuk az oszlop várható kifizetéseit. Így az ütközés valószínűsége a vegyes stratégiájú egyensúlyban 1/16.
A vegyes stratégiájú egyensúly bizonyos értelemben valószínűbb ebben a játékban: Ha a játékosok már tudnák, hogy ki fog engedni, akkor tulajdonképpen nem is kellene játszaniuk a játékot. A játék lényege, hogy kiderüljön, ki fog engedni, ami azt jelenti, hogy ez nem ismert előre. Ez azt jelenti, hogy a vegyes stratégiájú egyensúly bizonyos értelemben az ésszerűbb egyensúly.
16.19. ábra Kő, papír, olló
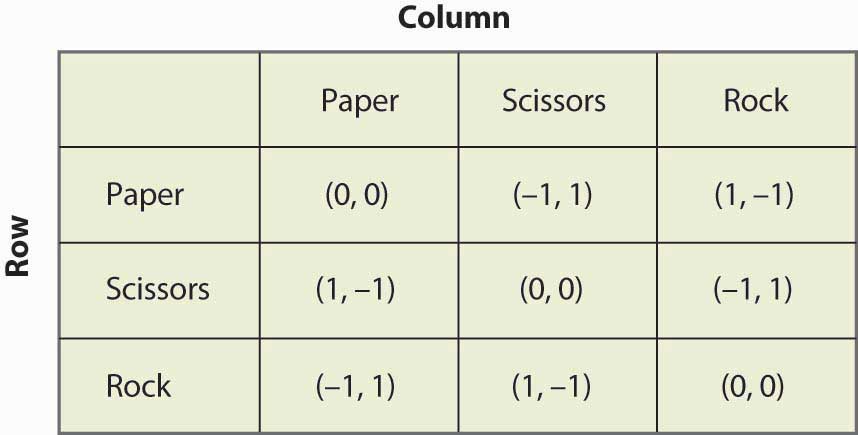
A “kő, papír, olló” egy olyan gyerekjáték, amelyben két gyerek a kezével egyszerre választja a papírt (laposan tartott kéz), az ollót (két ujját kiálló, ollónak látszó kéz) vagy a követ (ökölbe szorított kéz). A nyeremények jellege az, hogy a papír veri a követ, a kő veri az ollót, az olló pedig a papírt. Ez a játék a 16.19. “Kő, papír, olló” ábrán látható struktúrával rendelkezik.
Főbb tanulságok
- A vegyes stratégiájú Nash-egyensúlyban legalább egy játékos véletlenszerű stratégiát játszik, és egyetlen játékos sem tudja növelni a várható kifizetését alternatív stratégia játszásával.
- A véletlenszerűség nélküli Nash-egyensúlyt tiszta stratégiájú Nash-egyensúlynak nevezzük.
- Ha egy játékosnak két stratégiát kell véletlenszerűen választania, akkor mindkettőnek ugyanazt a várható kifizetést kell eredményeznie.
- A páros filléres játéknak van egy vegyes stratégiája és nincs tiszta stratégiája.
- A nemek harca játéknak van egy vegyes stratégiája és két tiszta stratégiája.
- A csirkejáték hasonló a nemek harcához, és ahhoz hasonlóan két tiszta stratégiája és egy vegyes stratégiája van.
GYakorlatok
- Legyen q annak a valószínűsége, hogy Row fejet játszik. Mutassuk meg, hogy Oszlop akkor és csak akkor hajlandó randomizálni, ha q = ½. (Tipp: Először számítsuk ki az Oszlop várható nyereményét, ha az Oszlop fejet játszik, majd számítsuk ki az Oszlop várható nyereményét, ha az Oszlop írásjelet játszik. Ezeknek egyenlőnek kell lenniük ahhoz, hogy oszlop randomizáljon.)
- Mutassuk meg, hogy a kő-papír-olló játékban nincsenek tiszta stratégiájú egyensúlyok. Mutassuk meg, hogy mindhárom akció egyenlő valószínűséggel való lejátszása vegyes stratégiájú egyensúly.
-
Keresd meg a következő játékok összes egyensúlyát:
16.20. ábra
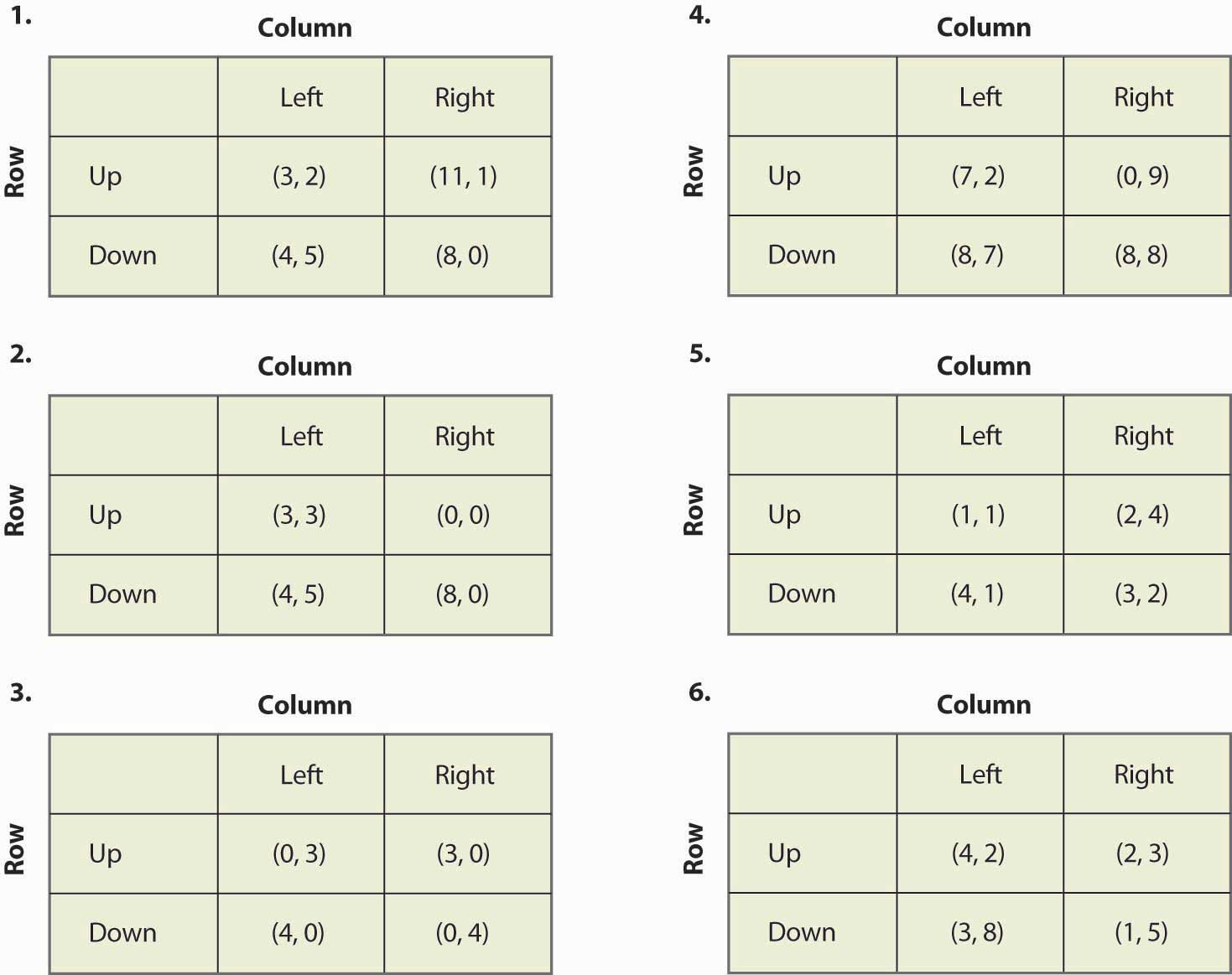
- Ha egy játékos nyereményét megszorozzuk egy pozitív konstanssal, a játék egyensúlyai nem változnak. Ez igaz vagy hamis, és miért?