A blokkdiagramok egyetlen blokkból vagy blokkok kombinációjából állnak. Ezeket a vezérlőrendszerek képi formában történő ábrázolására használják.
A blokkdiagram alapelemei
A blokkdiagram alapelemei a blokk, az összegzési pont és a levételi pont. Tekintsük a következő ábrán látható zárt hurkú szabályozórendszer blokkdiagramját, hogy azonosítani tudjuk ezeket az elemeket.
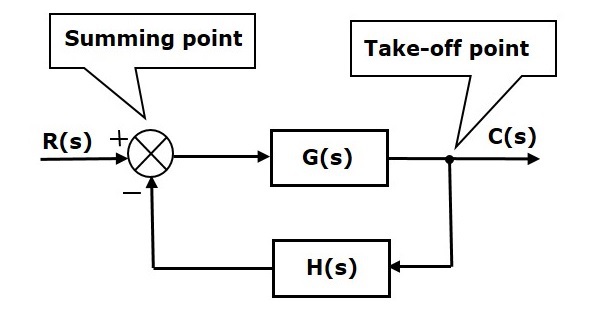
A fenti blokkdiagram két blokkból áll, amelyek G(s) és H(s) átviteli függvényekkel rendelkeznek. Ezen kívül van egy összegzési pont és egy felszállási pont. A nyilak a jelek áramlásának irányát jelzik. Most egyenként tárgyaljuk ezeket az elemeket.
Blokk
A komponens átviteli függvényét egy blokk ábrázolja. A blokk egyetlen bemenettel és egyetlen kimenettel rendelkezik.
A következő ábrán egy olyan blokk látható, amelynek bemenete X(s), kimenete Y(s) és az átviteli függvény G(s).

Transzferfüggvény,$G(s)=\frac{Y(s)}{X(s)}$
$$\Jobboldali nyíl Y(s)=G(s)X(s)$$
A blokk kimenetét a blokk transzferfüggvényének a bemenettel való szorzásával kapjuk.
összegző pont
Az összegző pontot egy körrel ábrázoljuk, amelyben kereszt (X) van. Két vagy több bemenettel és egyetlen kimenettel rendelkezik. A bemenetek algebrai összegét állítja elő. A bemenetek összegzését vagy kivonását vagy az összegzés és kivonás kombinációját is elvégzi a bemenetek polaritása alapján. Nézzük meg ezt a három műveletet egyenként.
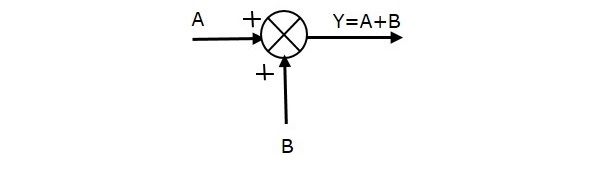
A következő ábra az összegzőpontot mutatja két bemenettel (A, B) és egy kimenettel (Y). Itt az A és B bemenetek pozitív előjelűek. Tehát az összegző pont az Y kimenetet A és B összegeként állítja elő.
azazaz,Y = A + B.
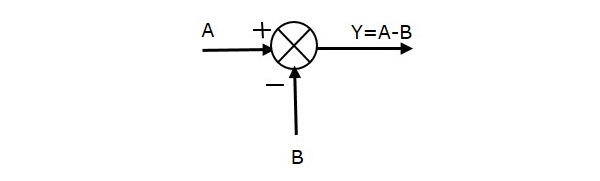
A következő ábra az összegző pontot mutatja két bemenettel (A, B) és egy kimenettel (Y). Itt az A és B bemenetek előjele ellentétes, azaz A pozitív előjelű, B pedig negatív előjelű. Tehát az összegző pont az Y kimenetet A és B különbségeként állítja elő.
Y = A + (-B) = A – B.
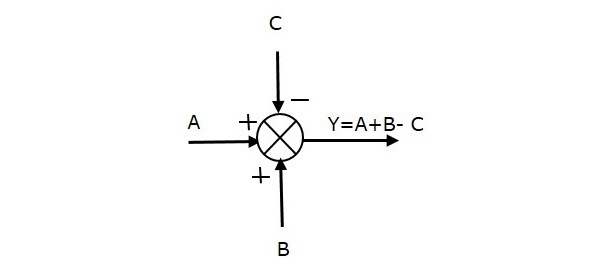
A következő ábra az összegző pontot mutatja három bemenettel (A, B, C) és egy kimenettel (Y). Itt az A és B bemenetek pozitív előjelűek, C pedig negatív előjelű. Tehát az összegző pont az Y kimenetet a következőképpen állítja elő:
Y = A + B + (-C) = A + B – C.
A leválasztási pont
A leválasztási pont egy olyan pont, ahonnan ugyanaz a bemeneti jel több ágon is átvezethető. Ez azt jelenti, hogy az átvételi pont segítségével ugyanazt a bemenetet egy vagy több blokkhoz, összegző ponthoz juttathatjuk.
A következő ábrán az átvételi pontot arra használjuk, hogy ugyanazt a bemenetet, R(s) két további blokkhoz kapcsoljuk.
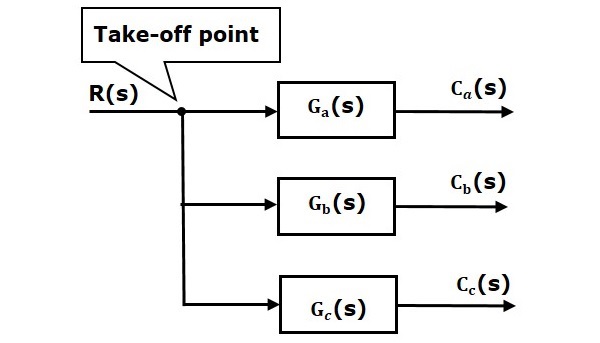
A következő ábrán az átvételi pontot arra használjuk, hogy a C(s) kimenetet, mint az egyik bemenetet összekapcsoljuk az összegző ponttal.
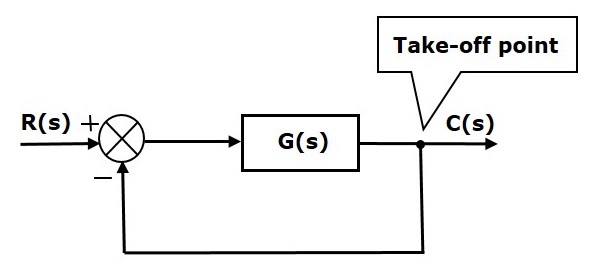
Elektromos rendszerek blokkdiagramszerű ábrázolása
Ebben a részben ábrázoljunk egy elektromos rendszert blokkdiagrammal. Az elektromos rendszerek főként három alapelemet tartalmaznak: ellenállás, induktor és kondenzátor.
Fogadjunk fel egy RLC-sorozatú áramkört a következő ábrán látható módon. Ahol Vi(t) és Vo(t) a bemeneti és kimeneti feszültségek. Legyen i(t) az áramkörön áthaladó áram. Ez az áramkör időtartományban van.
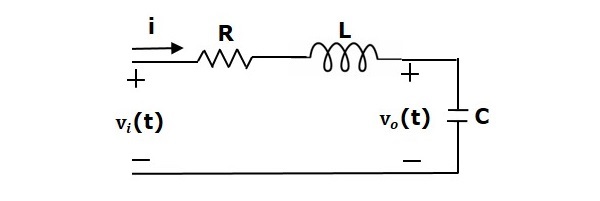
A Laplace-transzformációt alkalmazva erre az áramkörre, megkapjuk az áramkört az s-tartományban. Az áramkör a következő ábrán látható.
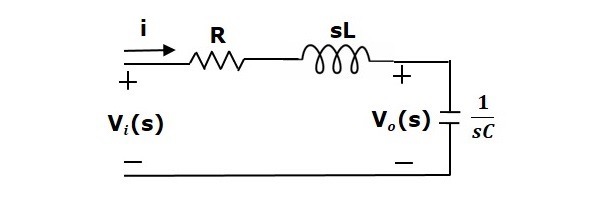
A fenti áramkörből felírhatjuk
$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$
$\Jobbra I(s)=\balra \{ \frac{1}{R+sL}{R+sL} \right \}\left \{ V_i(s)-V_o(s) \right \}$ (1. egyenlet)
$V_o(s)=\left ( \frac{1}{sC} \right )I(s)$ (2. egyenlet)
Rajzoljuk most a két egyenlet blokkdiagramját külön-külön. Majd kombináljuk ezeket a blokkdiagramokat megfelelően, hogy megkapjuk az RLC áramkör sorozatának teljes blokkdiagramját (s-tartomány).
Az 1. egyenletet egy olyan blokkal lehet megvalósítani, amelynek átviteli függvénye $\frac{1}{R+sL}$. Ennek a blokknak a bemenete és kimenete $\left \{ V_i(s)-V_o(s) \right \}$ és $I(s)$. Szükségünk van egy összegző pontra, hogy megkapjuk $\left \{ V_i(s)-V_o(s) \right \}$. Az 1. egyenlet blokkdiagramja a következő ábrán látható.
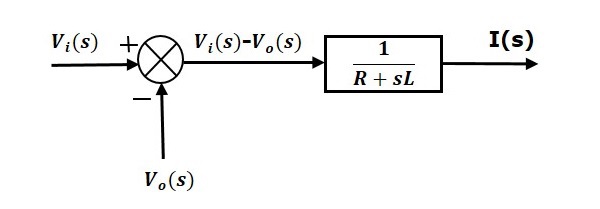
A 2. egyenlet egy olyan blokkal valósítható meg, amelynek átviteli függvénye $\frac{1}{sC}$. Ennek a blokknak a bemenete és kimenete $I(s)$ és $V_o(s)$. A 2. egyenlet blokkdiagramja a következő ábrán látható.
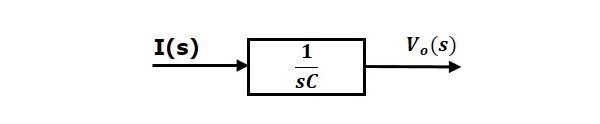
Az RLC áramkör (s-tartomány) sorozatának teljes blokkdiagramja a következő ábrán látható.
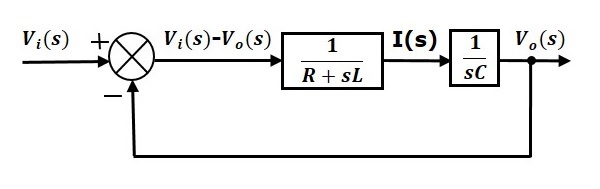
Hasonlóképpen, bármely elektromos áramkör vagy rendszer blokkdiagramját megrajzolhatja, ha csak ezt az egyszerű eljárást követi.
-
Az időtartománybeli elektromos áramkört Laplace-transzformáció alkalmazásával s-tartománybeli elektromos áramkörré alakítja át.
-
Írd fel az összes soros ági elemen áthaladó áram és az összes mellékágon áthaladó feszültség egyenleteit.
-
Rajzold fel egyenként a fenti egyenletek blokkdiagramjait.
-
Ezeket a blokkdiagramokat megfelelően kombinálja, hogy megkapja az elektromos áramkör teljes blokkdiagramját (s-tartomány).