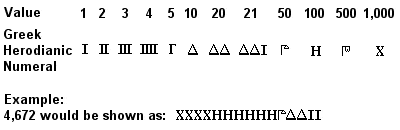
Ancient Greek Herodianic numerals
ギリシャ帝国は小アジアに影響範囲を広げ始めていました。 メソポタミアやそれ以外の地域でも、ギリシア人は征服した社会から有用な要素を取り入れ、適応させるのに十分な知恵を持っていた。 これは数学にも言えることで、バビロニアとエジプトの両方から数学の要素を取り入れた。 しかし、彼らはすぐに独自の重要な貢献をするようになり、初めて個人による貢献を認めることができるようになった。
Attic or Herodianic numerals
Attic or Herodianic numeralsとして知られている古代ギリシャの数字システムは、完全に紀元前450年までに開発し、おそらく紀元前7世紀には通常の使用されていた。 古代ギリシャの数詞体系は、紀元前450年頃に完成し、おそらく紀元前7世紀頃には常用されていた。この体系は、それ以前のエジプト式数詞体系(後のローマ式数詞体系にさらに類似)に似た10の基数を持ち、1、5、10、50、100、500、1000の記号を必要な数だけ繰り返して表現する。 足し算は足す数の記号(1s、10s、100sなど)を別々に合計することで行われ、掛け算は連続した2倍を基本とする手間のかかる作業だった(割り算はこの逆の作業)。
Thales’ Intercept Theorem
Thales’ Intercept Theorem
しかし、ギリシャ数学のほとんどは幾何学に基づいていたのである。 紀元前6世紀前半に小アジアのイオニア海岸に住んでいた古代ギリシャの七賢人の一人タレスは、通常、幾何学の抽象的発展のためのガイドラインを最初に定めたと考えられているが、彼の仕事について我々が知っていることは(相似三角形や正三角形など)今では非常に初歩的に思えることである。
タレスは、長辺を円の直径とする円の中に三角形を描くと、その対角は必ず直角になる(また、そこから派生するいくつかの関連する性質)という、タレスの定理として知られるものを打ち立てた。 また、2本の直線が平行線と交差したときにできる線分の比(ひいては相似な三角形の辺の比)についての定理(タレスの定理、インターセプト定理とも呼ばれる)もある。 実際、彼は「哲学」(「知恵を愛すること」)と「数学」(「学ぶこと」)の両方の言葉をつくったと考えられている。 ピタゴラスは、幾何学的要素と数が対応する完全な数学体系が構築できることを、おそらく最初に認識した人物である。 ピタゴラスの定理(またはピタゴラスの定理)は、あらゆる数学の定理の中で最もよく知られたものの一つである。 しかし、後述するように彼は依然として論争の的となる人物であり、ギリシャの数学は決して一人の人物に限定されたものではなかったのである。
Three geometrical problems
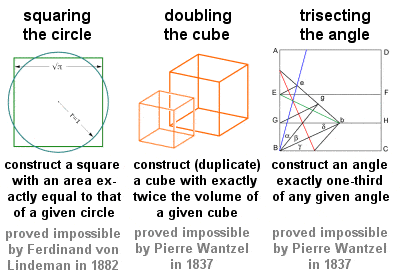
The Three Classical Problems
Three geometrical problems, often referred to the Three Classical Problems, and all to solve by purely geometric means using a straight edge and a compass, dates back to the early days of Greek geometry.All the Three Classical problemsは、特に3つの幾何学の問題で、直線とコンパスだけで、解決することができる。 「円の2乗(または求積)」「立方体の2倍(または複製)」「角の3等分」である。 これらの難問は、後の幾何学に大きな影響を与え、多くの有益な発見をもたらしましたが、実際の解決(あるいは不可能であることの証明)は19世紀まで待たねばなりませんでした。 詳しい経歴はこちら)、紀元前5世紀にこれらの問題に取り組んだギリシャの数学者の一人です(「円の二乗」問題に対する彼の貢献は「ヒポクラテスのリューネ」として知られています)。 紀元前440年頃の著書『元素』は、幾何学の要素を初めてまとめたもので、ユークリッドの後の著作の重要な資料となるなど、影響を与えた。
ゼノンの「アキレスと亀のパラドックス」
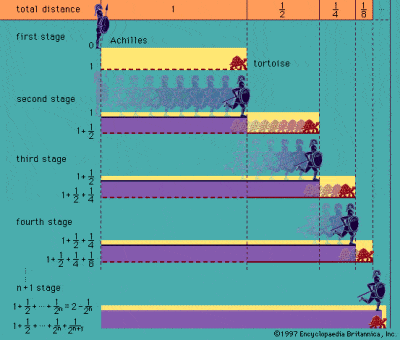
ゼノンの「アキレスと亀のパラドックス」
前5世紀の哲学者エラのゼノンによる有名なパラドックスで述べられているように、最初に無限という概念に取りくんだのはギリシャ人であった。 ゼノンのパラドックスで最も有名なのは、「アキレスと亀」である。 アキレスは足の遅い亀を先に走らせるが、アキレスが亀のスタート地点に着いた時には、亀はすでに先に進んでいる。
このようなパラドックスやゼノンのいわゆる二項対立のパラドックスは、空間と時間の無限の分割可能性に基づいており、半分と4分の1と8分の1と16分の1など、無限に続くものは決して全体と一致しないという考えに基づいています。 しかし、このパラドックスは、有限の時間内に無限の数の離散的なダッシュを完成させることは不可能であるという誤った仮定に起因するものであるが、その誤りを決定的に証明することは極めて困難である。 特に、古代ギリシャのアリストテレスは、無限は潜在的なものであり、実在しないと固く信じていたので、パラドックスを反証しようとした最初の人物であった。
すべての物質は小さな原子からできているという先見の明で有名なデミクリトスは、紀元前5世紀から4世紀にかけて数学と幾何学の先駆者でもあり、「数について」「幾何学について」「接線について」「地図について」「イラプションについて」といったタイトルの作品を発表したが、これらの作品は現存していない。 円錐(またはピラミッド)が同じ底辺と高さの円柱(またはプリズム)の3分の1の体積を持つことを最初に観察したこと、物体を無限の断面に分割することを真剣に考えたのはおそらく彼が最初であろうことが分かっている。
しかし、特にピタゴラスが、前387年にアテネに有名なアカデミーを設立したプラトンや、その弟子のアリストテレスなど、後輩たちに大きな影響を与えたことは確かで、彼の論理学の研究は2000年以上も決定的なものとして扱われた。 プラトンの弟子であるクニドスのエウドクソスは、ピラミッドと円錐の体積の計算に使用した連続近似による積分の初期の方法である「消耗法」(後にアルキメデスが開発)を最初に実施したと通常信じられています。 また、2つの整数の比として表現できない非合理な大きさにも、有理な大きさにも適用できる一般的な比例論を展開し、ピタゴラスの不完全な考えを発展させた。
| < エジプト数学へ戻る | ピタゴラスへ戻る > |