Chemguide: CIE A level Chemistryのサポート
学習成果 11.2(f)
この文は分配係数についてです。
先に進む前に、シラバスのコピーからこの文を見つけて読んでおくと良いでしょう。
分配
エーテルと水のような2つの混じり合わない液体があり、分液ロートで振ると、明らかに2つの層を形成する。
ここで、エーテルと水の混合物を振って、両方に溶ける物質を入れたとする。 物質Xは水よりもエーテルに溶けやすいとしよう。
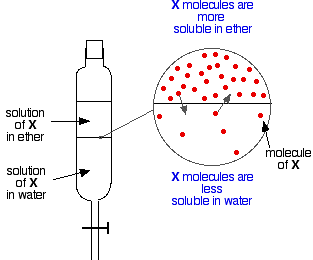
Xの粒子は2つの液体層の間の境界を横断し、すぐに動的平衡が設定されることになる。
上層に移動するすべての粒子に対して、1つは下層に移動します。
. 他の平衡と同じように、平衡定数を求めることができます：
この平衡定数は分配係数と呼ばれ、しばしば記号Kpcが与えられます：
他の平衡定数と同様に、分配係数は一定の温度で一定ですが、他のいくつかの制限も持っています。 かなり希薄な溶液に対してのみ正しく働き、溶質はどちらの溶媒でも同じ化学形態でなければならない。 反応したり、イオン化したり、会合したり（例えば二量体として一緒になる）してはいけません。
分配係数の計算
単位についての注意
分配係数は二つの濃度の単純な比であることに注意してください。
mol dm-3も使えますが、g cm-3 – grams per cubic centimetreを使うことが多いです。
技術的には角括弧はmol dm-3の濃度に対してのみ使用できますが、Application Support BookletとCIEのマークシートでは他の単位にも使用されています。
その覚悟がないので、標準以外の濃度単位が使われているところではなく、「Xの濃度」という言葉を使うことにします。
分配係数の計算
水100cm3にX1.00gを入れた溶液にエーテル10cm3を入れて振ると、エーテル層に0.80gが移行した。 エーテルと水の間のXの分配係数を計算しなさい。
二つの溶媒の間の分配係数を計算するように言われたら、最初に述べた溶媒の濃度がKpc式の上にくる。 つまりこの場合：
両方の濃度をg cm-3で計算できるだけの情報があります。
concentration of X in ether = 0.80/10 g cm-3
0.80gがイーサーに移ったとしたら1.00 – 0.80g = 0.80gがイーサーに移ったことになります。20gが水に残った。
水中のXの濃度 = 0.20/100g cm-3
だから：
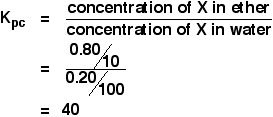
もちろん、式に入れる前に実際の数字としてエーテル中と水中の濃度を計算してもいいのですが、その場合は、水中の濃度が0.20/100g cm-3になります。 このような分配係数には単位がありません。上と下が同じなので、単位は相殺されます。 それを使って他のことを計算することについては、何も書いてありません。 これらの余分な計算はアプリケーションサポートブックレットで説明されており、2013年6月までの試験で2回（いずれも2009年）出題されています。
コースブックには（極めて適切に！）シラバスがそれについて触れていないため、この本はCIE試験委員からシラバスの「完全かつ正確なカバー」としてお墨付きを得ているのです。 ということは、CIEは今後一切出題しないということでしょうか？ 当てにしないでください！
基本的な例
前回と同じケースを使います-同じ溶媒、同じX、先ほど計算したばかりの分配係数です。
今回は、100cm3の水に1.00gのXを溶かした元の溶液を、5cm3のエーテルで振っていたら、どれだけエーテル層に抽出されたかを計算します。 これをmとします。
さて、エーテル中のXの溶液の濃度の式を計算してみましょう。
エーテル中のXの濃度＝m／5gcm-3
水はどうでしょう。 水には（1.00-m）gのXが残っていることになります。 ですから、
concentration of X in water = (1.00 – m)/100 g cm-3
さて、これをすべて分配係数の式に当てはめてみましょう。 すでにエーテルと水の間のXの分配係数を40と計算したことを思い出してください。
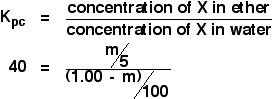
あとは簡単ですが、少し面倒な代数に直面します：
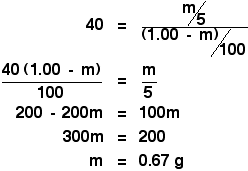
もっと面倒にしてください！
分配係数を求める最初の計算では、100 cm3 の水に 1.00 g の X を入れた元の溶液を 10 cm3 のエーテルで振ると 0.80 g の X が抽出されると言われました。
それを 5 cm3 のエーテルで振ると 0.67 g の X を抽出できると計算したところ、100 cm3 の水には 0.33 g のXが残りますね。 この溶液を大切に保管し、もう1回新しい5cm3のエーテルで振ったとします。
エーテルを10cm3ずつではなく、5cm3ずつ2回に分けて使うと、全部でどれくらいのXを取り出せるでしょうか。
2回目のエーテルで取り出したXの質量を、混乱しないようにnとします。
エーテル中のXの溶液の濃度の式を求めます。
concentration of X in ether = n/5 g cm-3
水はどうするのでしょう。 2回目の抽出で水には（0.33-n）gのXが残っていることになります。 つまり
concentration of X in water = (0.33 – n)/100 g cm-3
さて、これを先ほどのエーテルと水の間のXの分配係数の式に当てはめてみましょう。
つまり、5cm3のエーテル2ロットを合わせると、合計0.67＋0.22gのXを取り出したことになる。89gです。
もともと、エーテルを10cm3のロットで1回だけ行えば、0.80gしか抽出できないと言われていました。
上記のように溶媒を少量に分けることで、より効率的に抽出できます。有機化合物の調製の際には、このような手法を使うことがありますね。 水の中の面倒な溶液から、作ろうとしているものを抽出し、有機溶媒の中に終わらせるのです。
CIEでは、2009年6月のペーパー4問8でこれに似た問題が出題されました。 分配係数の値を計算し、それを使って上記と全く同じように2段階抽出をしなければなりませんでした。 この計算には4点の価値がありました。 面倒だし、（分配係数の計算を除けば）シラバスにも載っていない問題かもしれませんが、できないわけにはいかないでしょう
。
