はじめに
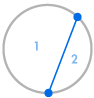
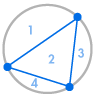
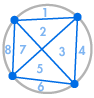
円の円周上にいくつかの点を置き、すべての点を互いに結ぶとします。 これは円を多くの異なる領域に分割し、それぞれの場合の領域の数を数えることができる。 下の図は、円周上にいくつかの異なる数の点があるとき、どれだけの領域があるかを示している。 私たちは、円の中のすべての交差点で、3つ以上ではなく、2つの線だけが出会うようにしなければならない。
 |
 |
 |
 |
 |
| 1 region | 2地域 | 4地域 | 8地域 | 16地域 |
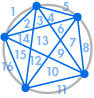
すぐにパターンが見えてくる。 これは、円周上の6つの点では32の領域があり、7つの点では64の領域があることを意味している。
私たちはこの結果で満足と判断するかもしれません。 領域の数は常に前の2倍である。結局、これは最初の5つのケースでうまくいった。
 |
 |
| 31 regions, not 32 | 57 regions, not 64 |
残念ながら何かが間違っていた:31は数え間違いに見えるかもしれませんが、57は64よりずっと少ないのです。 この例は、数学において、なぜ、ある観察が、テストしたいくつかのケースでうまくいったからといって、常に正しいとは言えないかを示しています。 その代わりに、すでに知っている結果から、真であることを示したい新しいものへと導く、厳密な論理的議論を考え出さなければならないのです。 そのような論証は証明と呼ばれる。
証明は、数学が他のすべての科学と異なる点であり、一度何かを証明すれば、それが常に真実であることが絶対に保証されるからである。 それは単に観測に合う理論ではなく、将来より良い理論に取って代わられるかもしれない。
上の例では、円の内側の交差点の数を数えることができた。 交点の数、線の数、領域の数の関係をよく考えると、やがてx=Vがあるときの領域の数について、別の式が導き出される。Axi点が円上にある場合:
Number of regions = x4 – 6 x3 + 23 x2 – 18 x + 2424 = (Math.pow(V.Axi,4) – 6*Math.pow(V.Axi,3) + 23*Math.pow(V.Axi,2) – 18*V.Axi + 24)/24.
この方程式は上のすべてのケースで動作します。
伝統的に、証明の終わりは■や□で示されるか、あるいはQEDや “quod erat demonstrandum”(ラテン語で「示されなければならなかったこと」の意)と書かれる。 それを証明すると、定理と呼ぶ。
公理

ラファエルのアテネ学派:古代ギリシャの数学者は、論理と公理の枠組みを使って数学にアプローチした最初の人たちだった。 まだ何も知らないのに、どうやって最初の定理を証明するのだろうか。 残念ながら、何もない状態で何かを証明することはできません。 これを公理と呼ぶ。
数学者は公理を証明することなく、それが真であると仮定する。 しかし、公理は定義か明らかに自明であり、非常に少数の公理しか存在しないので、これは見かけほど問題ではありません。 たとえば、任意の2つの数aとbに対して、a+b=b+aという公理があり得る。
公理は正しく理解することが重要で、数学のすべてがそれにかかっているからだ。 公理が少なすぎると、ほとんど証明できず、数学はあまり面白くなくなる。 公理が多すぎると、ほとんど何でも証明できてしまい、数学も面白くなくなる。 また、互いに矛盾する公理を持つこともできない。
数学は、正しい公理を選ぶことではなく、これらの出発点から枠組みを発展させることである。 異なる公理から始めれば、異なる種類の数学が得られるが、論理的な議論は同じになる。 数学のどの分野にも基本公理がある。
数学者は定理を証明すると、それを発表して他の数学者がチェックできるようにする。 論理的な議論に間違いが見つかることもあるし、何年も経ってから間違いが見つかることもある。
集合論と選択の公理

証明を定式化するために、数学が書かれる言語のまさに基礎に立ち返ることが必要な場合がある:集合論である。 集合の要素は通常、中括弧で書かれる。 2つの集合の和(どちらかの集合に含まれる要素の集合)を求めたり、2つの集合の交(両方の集合に含まれる要素の集合)を求めたりできる。
多くの数学的問題は集合論の言語で定式化でき、それを証明するには、集合論の公理が必要である。 長い間、数学者はさまざまな公理を使用してきたが、最も広く受け入れられているのは 9 つの Zermelo-Fraenkel (ZF) 公理である:
AXIOM OF EXTENSION
If two sets have the same elements, then they are equal.拡張公理は、2 つのセットが同じ要素を持つと、それらは等しい。
AXIOM OF SEPARATION
ある要素からなる集合の部分集合を形成することができる。

EMPTY SET AXIOM
メンバのない集合があり、{}または∅と表記される。
PAIR-SET AXIOM
二つの物体xとyがあるとき、集合{x, y}を形成できます。
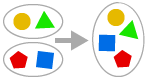
UNIONAXIOM
二つ以上の集合の和を形成することができるのです。
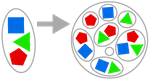
POWER SET AXIOM
任意の集合が与えられたとき、すべての部分集合の集合(冪集合)を形成できる。
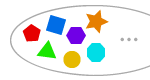
AXIOM OF INFINITY
要素が無限個である集合が存在する。

AXIOM OF FOUNDATION
集合はより単純な集合から構築され、すべての(空でない)集合には最小メンバーがあることを意味します。
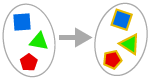
AXIOM OF REPLACEMENT
集合のすべての要素に関数を適用しても、答えは集合である
集合論について考えると、これらの公理のほとんどは完全に自明に思えるだろう–そしてこれが公理のあるべき姿なのだ。
AXIOM OF CHOICE
Given infinitely many non-empty sets, you can choose one element from each of these sets.
Axiom of Choice (AC) は一見すると、上記のものと同じように無害に見える。 しかし、無限大の使用は多くの予期せぬ結果をもたらす。 例えば、AC を使って、球体を5つに切り、それを組み立てて、それぞれ最初の球体と同じ2つの球体を作ることが可能であることを証明することができる。 これは理論的な概念に過ぎない。必要な切り口はフラクタルであり、現実には存在し得ないし、いくつかの破片は「測定不可能」であり、体積が定義されていない。 しかし、これらの不可能な切断を構成するために「選択の公理」が使えるという事実は、非常に興味深い。
論理学者の間では、「選択の公理」を認めるかどうか、熱い議論が交わされている。 公理の集まりはすべて小さな「数学的世界」を形成し、異なる世界では異なる定理が真となる可能性がある。 1つの球から2つの球を作ることができる世界に住んでいることが幸せかどうかということである。 nに適用される式をS(n)と呼ぶことにする。 数学的帰納法の4つのステップ:
- まず、S(1)が真であること、すなわちSが1に対して真であることを証明する。
- 次に、S(k)が真、すなわちある自然数kに対してSが真であるとする。
- この仮定を用いてS(k + 1)も真だと推測しようと試みる。 S(1)が真であることが分かっているので、S(2)も真でなければならない。 したがってS(3)は真でなければならない。 したがってS(4)は真でなければならない。 といった具合に。

帰納法はドミノ倒しに例えることができる。 最初のステップであるS(1)が真であることを証明することで、無限の連鎖反応が始まるのだ。 実はこれが非常に重要で、帰納的連鎖全体がこれに依存しているのです。
ハノイの塔の目的は、ある釘から別の釘に多数の円盤を移動することである。 一度に動かせるのは1枚の円盤だけで、小さい円盤の上に大きい円盤を置くことはできません。 できるだけ少ない移動回数で、最初のペグから最後のペグまで円盤の塔を移動させてください。
円盤の数。 Start Over ムーブ。 0
一度ゲームのルールを理解すると、任意の数の円盤があるとき、必要な最小のステップ数を見つけることができるようになります。 上のゲームで遊んでいると、n枚の円盤があれば、少なくとも2n – 1回の歩数が必要であることがわかるかもしれない。
S(1) が正しいのは明らかで、円盤が1枚なら1手だけで、21 – 1 = 1だからである。
さて、S(k) が正しい、つまり円盤がk枚なら2k – 1手必要だと仮定してみよう。 次に、k + 1 個のディスクがある場合:
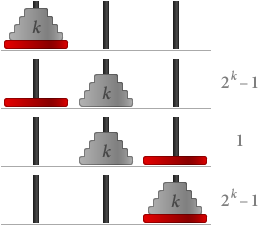
合計で (2k – 1) + 1 + (2k – 1) = 2(k+1) – 1 ステップが必要である。 これは、S(k + 1) も真であることを意味します。
数学的帰納法により、S(n) は n のすべての値に対して真で、これは n = V.Hanoi ディスクの最も効率のよい移動方法は、2n – 1 = Math.pow(2,V.Hanoi)-1 移動で済むということです。 6988>
最初のn個の自然数の和がn (n + 1)2であることを帰納法で証明してみよう。
1 = 1 (1 + 1)2.
1 + 2 = 2 (2 + 1)2 = 3.
次に、この結果がkについて正しい、つまり1 + 2 + … + k = k (k + 1)2 (kは指定しないいくつかの数)と仮定します。 ここで
1 + 2 + … + k + (k + 1) = k (k + 1)2 + (k + 1) = (k + 1) (k + 2)2 = (k + 1) 2.
あるkについて式が真なら、k + 1についても正しいことを今証明しました。 数学的帰納法により、この式はnのすべての値に対して真である。 6988>
上の方程式を証明する、帰納法を用いないもう一つの賢い方法があります。 歴史上最も偉大な数学者の一人であるカール・フリードリヒ・ガウス(1777-1855)が、小学生の時、先生に1から100までの整数をすべて足すように言われ、この方法を発見したと言われている。■6988>
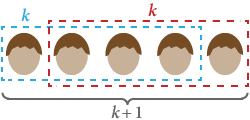
誘導を使って、人間はすべて同じ髪の色をしていることを証明したいと思う。
明らかにS(1)が正しい:1人だけの集団では、全員が同じ髪の色をしている。
次にS(k)を仮定する:k人の集団では、全員が同じ髪の色をしている。 ここでS(k)を仮定すると、k人の集団では全員が同じ髪の色になる。 これは、どのような初期グループにも当てはまり、k+1のグループも同じ髪の色であることを意味します。 したがってS(k + 1)は真である。
数学的帰納法により、すべての人間は同じ髪の色をしている!
数学的帰納法により、すべての人間は同じ髪の色をしている。
明らかに上の証明で何かが間違っているはずです。 6988>
定理の中には帰納法で証明できないものがあります。 S(k + 1)を証明するためにS(k)を仮定する代わりに、S(1), S(2), … S(k) をすべて仮定してS(k + 1)を証明するのです。 弱い)帰納法で証明できることはすべて強い帰納法でも証明できるが、その逆はない。
The Fundamental Theorem of Arithmeticとは1以上のすべての整数は素数か、もしくは本質的に唯一の方法で素数の積として記述できることを示すものである。
その一部を強い帰納法で証明できる。「整数nは素数であるか、素数の積として書くことができる」という記述をS(n)とする。 S(1)は例外だが、2は素数なのでS(2)は明らかに正しい。
ここで、ある整数kについて、S(1), S(2), …, S(k) が全て正しいと仮定しよう。k + 1は素数かk + 1より小さい因子を持つことが分かっている。 仮定により、これらの因数は素数の積として書けることが分かっている。 したがって、素数でない限り、k + 1も素数の積として書くことができる。 つまり、S(k + 1)は真である。
強帰納法により、S(n)は1より大きい数nすべてに対して真である。
この素因数分解が一意であることを証明するには、(因数の異なる順序を数えない限り)さらに作業が必要だが、特に難しいことではない。
このことから、弱い帰納法の原理と強い帰納法の原理は、それぞれが他のものを含意する、同等であることが分かる。 また、この2つは第3の定理である「整序の原理」と等価である:自然数の任意の(空でない)集合は、他のすべての要素よりも小さい最小の要素を持つ:
この整序の原理は自然数の定義的特徴である。 自然数![]() ={1, 2, 3, …}を定義するために用いられる基本公理の一つである。 これらの公理はイタリアの数学者ギゼッペ・ペアーノ(1858~1932)にちなんでペアーノ公理と呼ばれている。
={1, 2, 3, …}を定義するために用いられる基本公理の一つである。 これらの公理はイタリアの数学者ギゼッペ・ペアーノ(1858~1932)にちなんでペアーノ公理と呼ばれている。
矛盾による証明
矛盾による証明も重要な証明技法の一つである。 ある文Sを証明したい場合、Sが真でなかったと仮定する。 この仮定を使って、0=1のような誤った結果を演繹してみる。 もし、すべての手順が正しく、結果が偽であれば、最初の仮定が間違っていたのでしょう。 このテクニックは、√2が不合理であることの証明、実数が数えられないことの証明、素数が無限にあることの証明など、さまざまな状況で使用することができる。
もう一つ楽しい例を挙げよう:
矛盾による証明と整列の原理を使って、すべての自然数が「面白い」ことを証明できる。
すべての自然数は面白くないとし、面白くない数の集合をSとする。 井戸端会議の原理により、Sには最小のメンバーxがあり、それは最小の非面白い数である。 この不思議な性質は、明らかにxを特に面白い数にしている。 これはxが非関心であると仮定していたので矛盾している。
したがって、すべての数は興味深いのである。 ゲーデルと証明不可能な定理

Kurt Gödel (1906-1978)
20世紀初頭、数学は急速に発展し始め、数千人の数学者が無数の新しい分野で研究を行っていました。 ヒルベルト(1862~1943)は、数学を形式化し、数学の基礎にある矛盾を解決するための大規模なプログラムを立ち上げた。 これには、単純で普遍的な公理のセットを使ってすべての定理を証明すること、この公理のセットが一貫していることを証明すること、この公理のセットが完全であること、つまり、公理を使ってあらゆる数学的記述を証明または反証できることを証明することが含まれていました。 彼は、ある公理を持つどんな(十分に複雑な)数学体系でも、その公理を使って証明も反証もできないいくつかの文を見つけることができることを証明したのです。 また、ある公理群が矛盾しないことを、その公理群以外を使って証明することもできない。
ゲーデルの発見は、ある公理群が矛盾しないかどうかなど、それ自身について何かを言うために使うことができないという事実に基づいている。 自己言及の問題は、数学だけでなく、言語でも見られる。 以下はライアー・パラドックスです:
「この文は偽である」
上の文はそれ自身について何かを言おうとしているのです。 もしそれが真実なら、この文はそれが偽であることを教えてくれる。 もしそれが偽であれば、この文はそれが偽でないこと、すなわちそれが真であることを教えてくれます。
ゲーデルの定理が最初に発表されたとき、多くの数学者は深く悩んだ。 ある観測結果を証明しようとするとき、証明が存在するかどうかわからない、つまり、結果は真であっても証明不可能であるかもしれない。 今日、不完全性は論理学だけでなく、論理演算を行う機械に依存するコンピューターサイエンスの基本的な部分であることが分かっている。 その一例が、無限集合の大きさに関する「連続体仮説」である。
晩年、クルト・ゲーデルは重度の精神障害を発症し、1978年に自死を遂げた。 論理学の基礎に関する彼の洞察は、古代ギリシャ人による証明の発展以来、最も深いものであった
。