ブロック図は単一のブロックまたはブロックの組み合わせから構成されています。 これらは、制御システムを絵で表現するために使用される。
ブロック図の基本要素
ブロック図の基本要素は、ブロック、和算点、離接点である。 下図のような閉ループ制御系のブロック図を考えて、これらの要素を確認してみましょう。
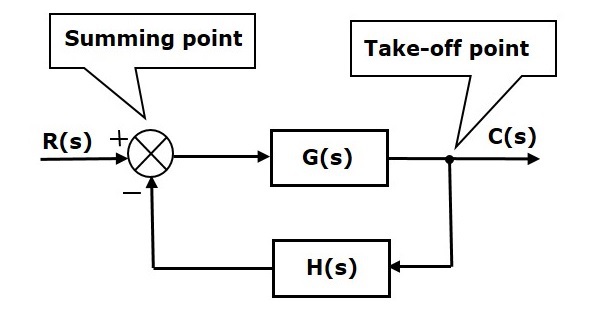
上のブロック図は、伝達関数G(s)、H(s)を持つ2つのブロックから構成されています。 また、1つの和算点と1つの離脱点を有している。 矢印は信号の流れる方向を示しています。
ブロック
部品の伝達関数はブロックで表されます。 下図は入力X(s)、出力Y(s)、伝達関数G(s)を持つブロックです。

伝達関数,$G(s)=Thatfrac{Y(s)}{X(s)}$
$Rightarrow Y(s)=G(s)X(s)$$
伝達関数とブロックの入力を乗じることによりブロックの出力は求まります。
Summing Point
円内に十字(X)があるものをSumming Pointという。 2つ以上の入力と1つの出力がある。 入力の代数的な和を生成する。 また、入力の極性に基づいて、入力の和または減算、あるいは和と減算の組み合わせを実行する。 この3つの演算を一つずつ見ていきましょう。
下図は、2つの入力(A、B)と1つの出力(Y)の和算点を示しています。 ここで、入力A、Bは正の符号を持つ。 つまり、和周波点はAとBの和として出力Yを生成する。
すなわち、Y = A + B.
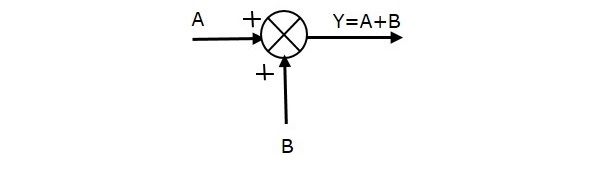
次の図は、2つの入力(A、B)と1つの出力(Y)の和周波点である。 ここで、入力AとBは反対の符号、つまり、Aは正の符号、Bは負の符号を持つ。
Y = A + (-B) = A – B.
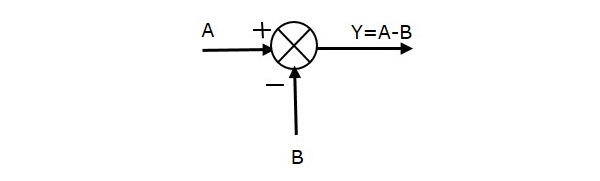
次の図は、3つの入力(A、B、C)と1つの出力(Y)を持つ和算点を示している。 ここで、入力AとBは正符号、Cは負符号である。 したがって、和算点は出力Yを
Y = A + B + (-C) = A + B – C.と生成する。
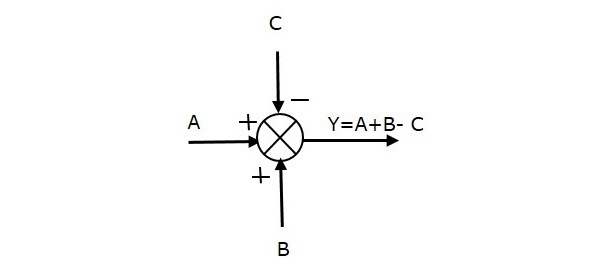
Take-off Point
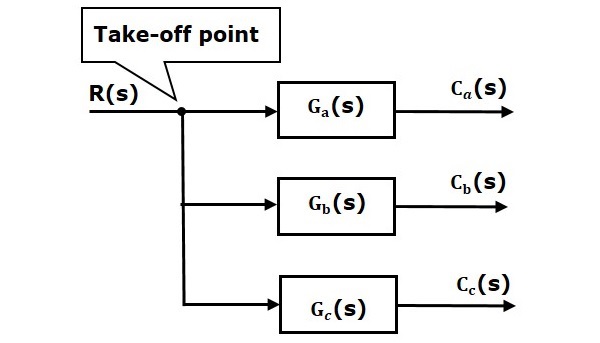
離脱点とは、同じ入力信号を複数の分岐に通過させることができる点である。
下図では、テイクオフポイントを使用して、同じ入力Rをさらに2つのブロックに接続している。
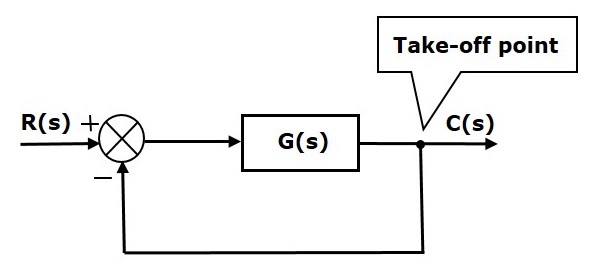
次の図では、テイクオフポイントは、サミングポイントへの入力の1つである出力C(s)を接続するために使用される。
電気システムのブロック図表現
このセクションでは、電気システムをブロック図で表現してみましょう。 電気系には主に抵抗、インダクタ、コンデンサの3つの基本要素があります。
下図のような直列のRLC回路を考えてみましょう。 ここで、Vi(t)とVo(t)は入力電圧と出力電圧である。 i(t)は回路を通過する電流とする。 この回路は時間領域です。
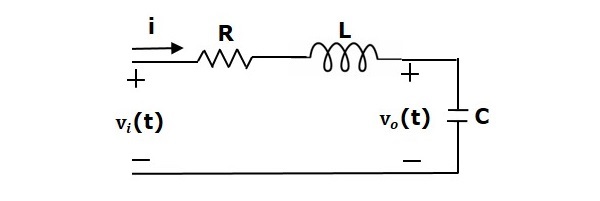
この回路にラプラス変換をかけると、S領域の回路が得られます。
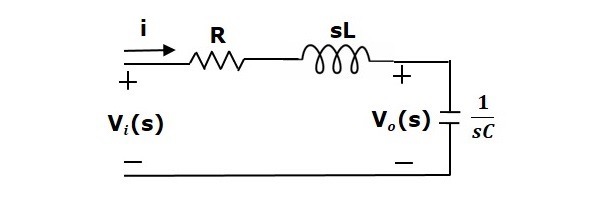
上記の回路から、
$I(s)=prac{V_i(s)-V_o(s)}{R+sL}$$
$Rightarrow I(s)=left \{frac{1}{R+sL}} {3866>$S(s) {3866}$I(s)=prac{1}{R+sL} {3866}$$と書くことができる。 \V_i(s)-V_o(s) \right }$ (式1)
$V_o(s)=left ( \frac{1}{sC} \right )I(s)$ (式2)
ここで、この二つの式のブロック図をそれぞれ描いてみましょう。
式1は伝達関数$frac{1}{R+sL}$を持つブロックで実現できます。 このブロックの入出力は$left \{ V_i(s)-V_o(s) \right \}$と$I(s)$である。 また、$left \{ V_i(s)-V_o(s) \right \}$ を得るために和算点が必要である。 式1のブロック図を下図に示す。
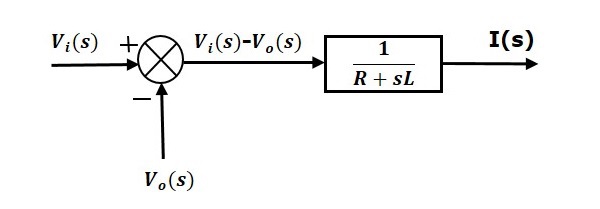
式2は伝達関数$frac{1}{sC}$を持つブロックで実装することが可能である。 このブロックの入力と出力は$I(s)$と$V_o(s)$である。
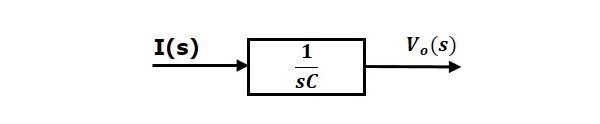
直列RLC回路(s領域)の全体ブロック図を下図に示します。
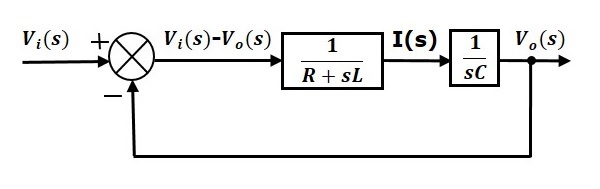
同様に、この簡単な手順であらゆる電気回路やシステムのブロック図を描くことができます。
-
時間領域の電気回路をラプラス変換してs領域の電気回路に変換する。
-
すべての直列分岐素子に流れる電流とすべての分枝にかかる電圧の式を書き出す。
-
上記の式をすべて個別にブロック図にする。
-
これらのブロック図をすべて正しく組み合わせて、電気回路(S領域)の全体的なブロック図を得る。