16.3 混合戦略
学習の目的
- 解の一部としてランダム化を必要としたり認めたりするゲームは?
図16に示すように、再びペニー合わせゲームについて考えてみましょう。図16.13「再びマッチングペニー」
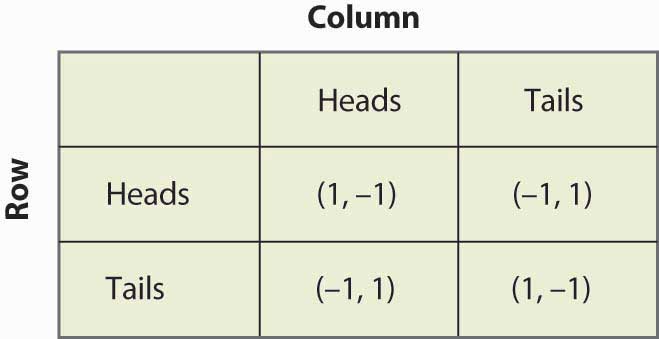
列が確率pで表を出すと考えたとする。 同様に、列がヘッズをプレイした場合、確率pで-1、確率(1 – p)で1、期待値は1 – 2pとなる。 これを図16.14「ペニー合わせの混合戦略」にまとめる。
2p – 1 > 1 – 2pであれば、平均して行はテールよりヘッズをプレイした方が良いということになる。 同様に、2p – 1 < 1 – 2pなら、RowはHeadsよりTailsをプレイした方が良い。 一方、2p – 1 = 1 – 2pであれば、Rowが何をやっても同じペイオフになります。 この場合、RowはHeadsをプレイすることも、Tailsをプレイすることも、コインをはじいてRowのプレイをランダムにすることもできる。
A mixed strategy Nash equilibrium少なくとも1人がランダム化戦略をプレイし、どのプレイヤーも代替戦略をプレイして自分の期待ペイオフを増やすことができないナッシュ均衡。 少なくとも1人がランダム化戦略をプレイし、どのプレイヤーも代替戦略をプレイして自分の期待ペイオフを増やすことができることを含む。 このようなナッシュ均衡を純粋戦略ナッシュ均衡(pure strategy Nash equilibrium)と呼ぶ。8363>
Figure 16.14 Mixed strategy in matching pennies
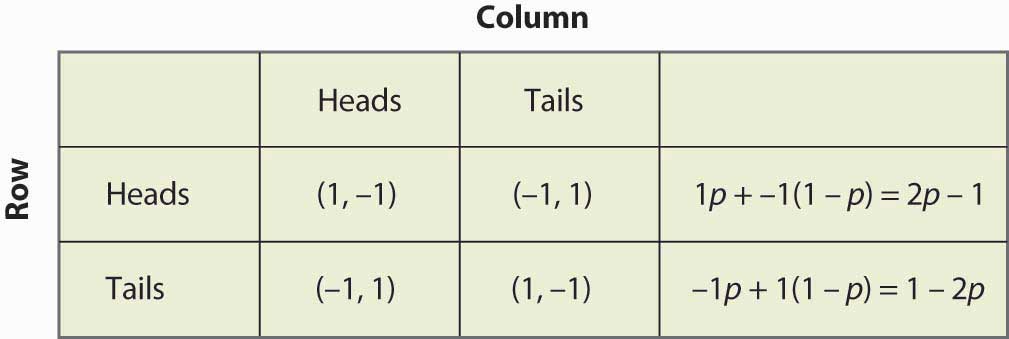
なお、ランダム化には期待ペイオフの等しさが求められる。 もしプレイヤーが戦略Aか戦略Bで無作為化するのであれば、これら2つの戦略は同じ期待ペイオフを生み出さなければならない。
混合戦略の計算には、しばしば混乱する要素が1つある。 Rowがランダム化するとする。 すると、Rowが正の確率でプレイするすべての戦略でRowのペイオフは等しくなければならない。 しかし、Rowのペイオフが等しいからといって、Rowが様々なRowをプレーする確率が決まるわけではありません。 その代わりに、行のペイオフが等しいことで、列が様々な列をプレーする確率が決まるのです。 Rowがランダム化するのであれば、Columnの確率はRowがランダム化してもよいと思うようなものでなければなりません。
従って、例えば、RowがHeadsをプレイした場合のペイオフを計算すると、2p – 1となり、pはColumnがHeadsをプレイする確率となります。 同様に、列が尾を演じる場合のペイオフは1 – 2pである。 列はこれらが等しいならランダム化してもよいと考え、p = ½と解きます。
さて、もう少し難しい例で、男女の戦いに再挑戦してみましょう。 図16.15「男女の戦いにおける混合戦略」にもう一度ペイオフを示します。
Figure 16.15 Mixed Strategy in battle of the sexes
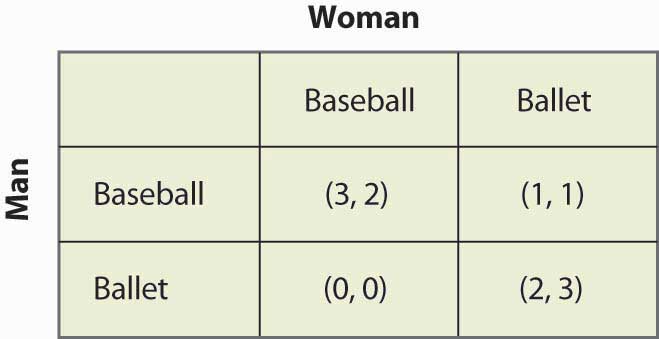
このゲームには2つの純粋戦略ナッシュ均衡があります。 (Baseball,Baseball)と(Ballet,Ballet)の2つの純粋戦略ナッシュ均衡がある。 混合戦略はあるのだろうか。 混合戦略を計算するために、女性は確率pでベースボールゲームに行き、男性は確率qでベースボールゲームに行くとします。図16.16「混合戦略の完全計算」には各プレイヤーの混合戦略のペイオフの計算が含まれています
Figure 16.16 混合戦略の完全計算
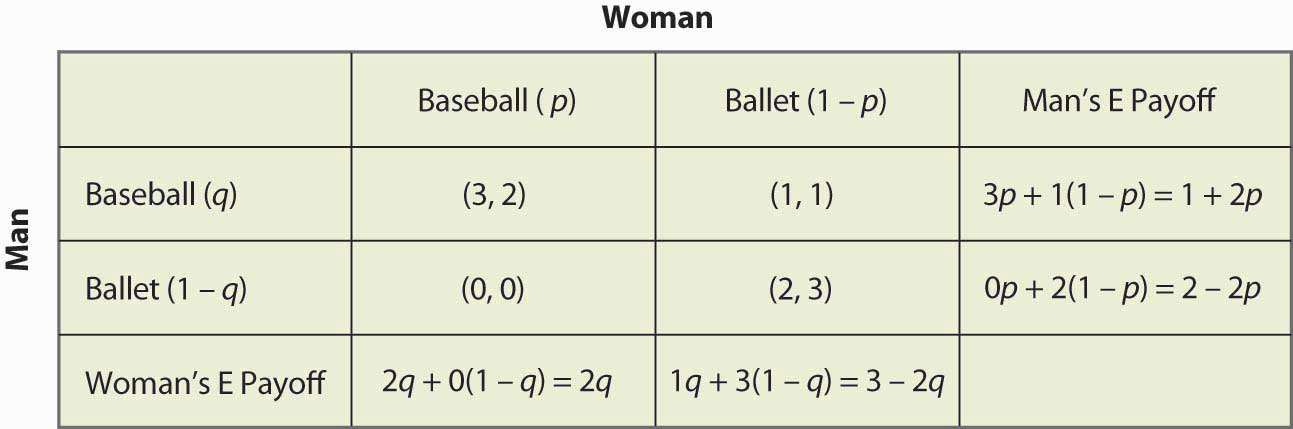
例えば、男(行のプレイヤー)が野球の試合に行くと、女が野球の試合に行ったとき(確率p)は3、それ以外は1で、期待ペイオフは3p + 1(1 – p) = 1 + 2pとなる。
Battle of the Sexesゲームにおける混合戦略は、両者がランダム化する必要がある(どちらかが純粋な戦略をとると、もう一方がランダム化できなくなるため)。 野球に行くかバレーに行くかの無関心は、1 + 2p = 2 – 2pを要求し、p = ¼となる。 つまり、男は、女が3/4以上の確率でバレエに行き、そうでなければ野球の試合に行くのであれば、どちらのイベントに行くかをランダムにすることをいとわないのである。 この場合、男は女と一緒にいることを好むが、野球の試合にも出たいので、2つのイベントの間に無関心になる。
同様に、女性がランダム化するためには、女性は野球の試合に行くこととバレエに行くことから等しいペイオフを得る必要があり、それには2q = 3 – 2q、つまりq = ¾が必要である。 したがって、男が野球の試合に行く確率は¾であり、バレエに行く確率は¼である。 これらは独立した確率なので、両方が野球の試合に行く確率を求めるには、確率を掛け合わせれば、3/16となる。 図16.17「混合戦略の確率」は、4つの可能な結果すべての確率を記入する。
Figure 16.17 Mixed strategy probabilities
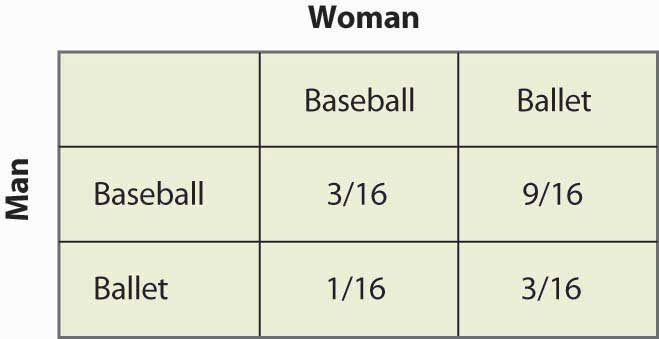
なお、半分以上の時間(野球、バレー)は混合戦略の結果で2人は一緒にいないことに注意してください。 このように協調しないことが、一般に混合戦略均衡の特徴である。 両プレイヤーの期待ペイオフも容易に計算できる。 男のペイオフは1 + 2p = 2 – 2pであり,p = ¼であるから,男は1½を得る. 同様の計算で、女性のペイオフも同じであることがわかる。 このように,両者とも,より好ましくない結果について調整するよりも悪い結果を得ることになる. しかし、この混合戦略ナッシュ均衡は、一見望ましくないが、相手の行動を考えると、どちらの当事者も自分のペイオフを改善できないという意味で、ナッシュ均衡である
男女の戦いでは、混合戦略ナッシュ均衡はありえないと思われ、カップルはより効果的に調整すると思われるかもしれない。 実際、電話をかけるだけで、混合戦略は排除されるはずである。 そこで、男女の戦いに関連した別のゲームを考えてみよう。そこでは、協調の失敗がより意味をなす。 これは、”チキン “のゲームである。 このゲームでは,2人のプレーヤーが互いに向かって車を走らせ,相手に譲るように説得し,最終的に溝に突っ込ませようとする. もし両方が溝に落ちたら、結果は引き分けとし、どちらも0点を得る。 一方がハンドルを切り、もう一方が切らなかった場合は、ハンドルを切った方が負け、もう一方が勝ちとなり、勝った方に1点を与える。プレーヤーのペイオフに定数を加えたり、プレーヤーのペイオフに正の定数をかけてもナッシュ均衡(純粋または混合)には影響しないことに注意すること。 したがって、各プレイヤーの結果を常に0とし、別の結果を1としておくことができる。 残る問題は、どちらも譲らない場合にどうなるかであり、その場合はクラッシュが発生する。 このバージョンでは、図16.18「チキン」に示すように、ペイオフはハンドルを切ったときの損失の4倍に設定されていますが、ゲームを変更してどうなるか見てみましょう。
Figure 16.18 Chicken
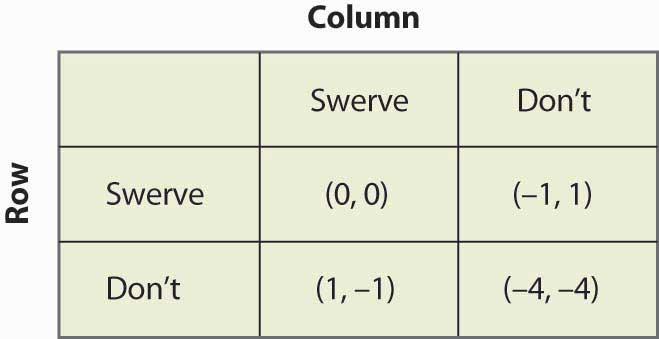
このゲームには二つの純粋戦略均衡があります。 (Swerve, Don’t)と(Don’t, Swerve)の2つの純粋戦略均衡がある。 また、混合戦略もある。 Columnが確率pでSwerveしたとすると、RowはSwerveすることで0p + -1(1 – p)、Swerveしないことで1p + (-4)(1 – p)、これらが等しければRowはランダム化するので、p = ¾が必要である。 つまり、混合戦略均衡においてColumnが横取りする確率は、¾である。 Rowが振り切る確率をqとし、Columnの期待ペイオフを計算することで、Rowプレイヤーが同じ確率を持つことが確認できる。 したがって、混合戦略均衡では衝突の確率は1/16となる。
このゲームではある意味、混合戦略均衡の方が可能性が高い。 もしプレイヤーが誰が降伏するか既に知っていたら、実際にゲームをする必要はない。 このゲームのポイントは、誰が降伏するかを見極めることであり、それは事前にはわからないということです。 8363>
Figure 16.19 Rock, paper, scissors
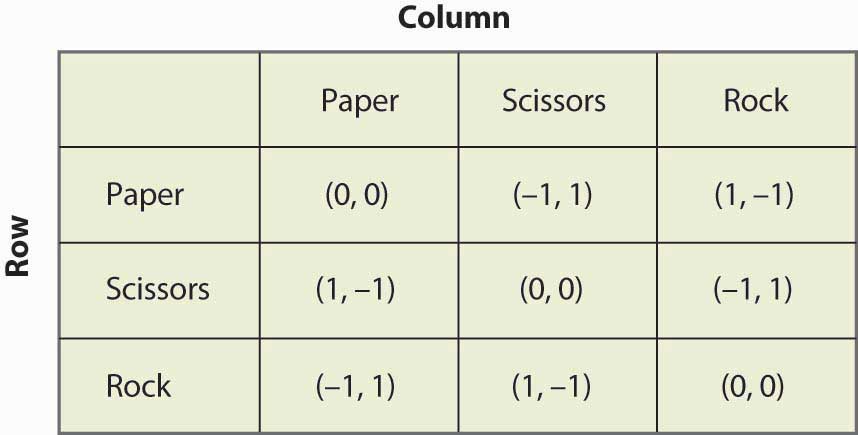
“Rock, paper, scissors” は2人の子供が手を使って同時に紙(手は平らに持つ)、はさみ(手は2本の指を突き出してはさみに見える)、石(手はこぶしで握る)を選ぶ子供のゲームである。 ペイオフの性質は、紙が岩に勝ち、岩がハサミに勝ち、ハサミが紙に勝つというものである。 このゲームは図16.19「ジャンケン」に示すような構造を持っている。
Key Takeaways
- 混合戦略ナッシュ均衡では、少なくとも1人のプレイヤーがランダム戦略をとり、どのプレイヤーも代替戦略をとって自分の期待ペイオフを高めることができない。
- プレイヤーが2つの戦略を無作為化する場合、どちらも同じ期待ペイオフを生み出す必要がある。
- マッチング・ペニーズ・ゲームは混合戦略で純粋戦略はない。
- チキンゲームは男女の戦いに似ていて、それと同じように2つの純粋戦略と1つの混合戦略がある。
ランダム化のないナッシュ均衡は純粋戦略ナッシュ均衡と呼ばれる。
演習
- 行が表をプレイする確率をqとする。 q = ½のときのみ、Columnがランダム化を希望していることを示せ。 (ヒント: まず、Column が Heads をプレイしたときの Column の期待ペイオフを計算し、次に Column が Tails をプレイしたときの Column の期待ペイオフを計算する。 コラムがランダム化するためには、これらが等しくなければならない)
- じゃんけんゲームにおいて、純粋戦略均衡が存在しないことを示せ。
- 3つの行動を同じ確率で行うことが混合戦略均衡であることを示せ。
Figure 16.20
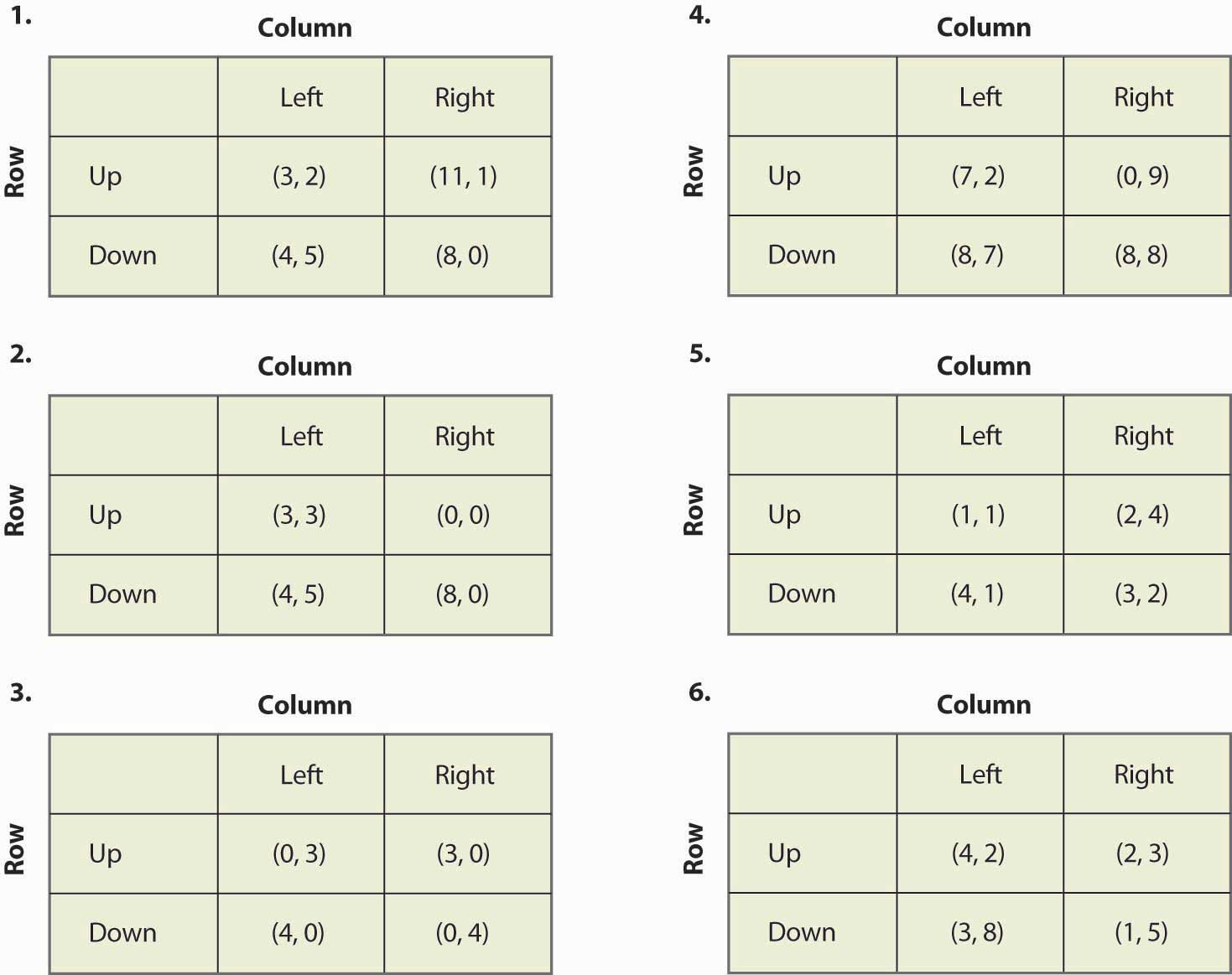
- あるプレイヤーの報酬に正の定数をかけても、そのゲームの均衡は変化しない。 これは真か偽か、そしてその理由は?