Inleiding
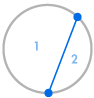
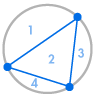
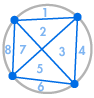
Stel je voor dat we verschillende punten op de omtrek van een cirkel plaatsen en elk punt met elkaar verbinden. Dit verdeelt de cirkel in veel verschillende regio’s, en we kunnen telkens het aantal regio’s tellen. De diagrammen hieronder laten zien hoeveel regio’s er zijn voor verschillende aantallen punten op de omtrek. We moeten ervoor zorgen dat op elk snijpunt binnen de cirkel slechts twee lijnen samenkomen, en niet drie of meer.
 |
 |
 |
 |
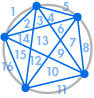 |
| 1 regio | 2 regio’s | 4 regio’s | 8 regio’s | 16 regio’s |
We kunnen onmiddellijk een patroon zien: het aantal regio’s is steeds het dubbele van het vorige, zodat we de reeks 1, 2, 4, 8, 16, … krijgen. Dit betekent dat met 6 punten op de omtrek er 32 regio’s zouden zijn, en met 7 punten 64 regio’s.
We zouden kunnen besluiten dat we tevreden zijn met dit resultaat. Het aantal regio’s is altijd het dubbele van het vorige – dit werkte immers voor de eerste vijf gevallen. Of we kunnen besluiten dat we er voor de zekerheid nog een paar moeten controleren:
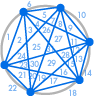 |
 |
| 31 regio’s, geen 32 | 57 regio’s, geen 64 |
Er is helaas iets misgegaan: 31 lijkt misschien een telfout, maar 57 is veel minder dan 64. De reeks gaat verder met 99, 163, 256, …, heel anders dan wat we zouden krijgen als we het vorige getal zouden verdubbelen.
Dit voorbeeld illustreert waarom je in de wiskunde niet zomaar kunt zeggen dat een waarneming altijd waar is, alleen maar omdat ze werkt in een paar gevallen die je hebt getest. In plaats daarvan moet je met een rigoureus logisch argument komen dat leidt van resultaten die je al kent, naar iets nieuws waarvan je wilt aantonen dat het waar is. Zo’n argument heet een bewijs.
Bewijzen zijn wat de wiskunde onderscheidt van alle andere wetenschappen, want als we eenmaal iets bewezen hebben, zijn we er absoluut zeker van dat het waar is en altijd waar zal zijn. Het is niet zomaar een theorie die past bij onze waarnemingen en in de toekomst vervangen kan worden door een betere theorie.
In bovenstaand voorbeeld zouden we het aantal snijpunten in de binnenkant van de cirkel kunnen tellen. Als we goed nadenken over het verband tussen het aantal snijpunten, lijnen en gebieden, komen we uiteindelijk tot een andere vergelijking voor het aantal gebieden als er x = V.Axi punten op de cirkel liggen:
Aantal gebieden = x4 – 6 x3 + 23 x2 – 18 x + 2424 = (Math.pow(V.Axi,4) – 6*Math.pow(V.Axi,3) + 23*Math.pow(V.Axi,2) – 18*V.Axi + 24)/24.
Deze vergelijking werkt in alle bovenstaande gevallen. We kunnen nu proberen om het voor elke waarde van x te bewijzen met behulp van “inductie”, een techniek die hieronder wordt uitgelegd.
Traditioneel wordt het einde van een bewijs aangegeven met een ■ of □, of door QED te schrijven of “quod erat demonstrandum”, wat Latijn is voor “wat moest worden aangetoond”.
Een resultaat of waarneming waarvan we denken dat ze waar is, noemen we een Hypothese of Conjectie. Zodra we het bewezen hebben, noemen we het een Stelling. Als we eenmaal een stelling bewezen hebben, kunnen we die gebruiken om andere, ingewikkelder resultaten te bewijzen – en zo een groeiend netwerk van wiskundige stellingen opbouwen.
Axioma’s

Raphaels School van Athene: de oude Griekse wiskundigen waren de eersten die de wiskunde benaderden met behulp van een logisch en axiomatisch kader.
Een interessante vraag is waar je moet beginnen. Hoe bewijs je de eerste stelling, als je nog niets weet? Helaas kun je niet iets bewijzen met niets. Je hebt op zijn minst een paar bouwstenen nodig om mee te beginnen, en die heten Axioma’s.
Mathematici nemen aan dat axioma’s waar zijn zonder ze te kunnen bewijzen. Dit is echter niet zo problematisch als het lijkt, omdat axioma’s ofwel definities zijn ofwel duidelijk voor de hand liggen, en er zijn maar heel weinig axioma’s. Een axioma zou bijvoorbeeld kunnen zijn dat a + b = b + a voor twee willekeurige getallen a en b.
Axioma’s zijn belangrijk om juist te zijn, want de hele wiskunde berust erop. Als er te weinig axioma’s zijn, kun je weinig bewijzen en zou wiskunde niet erg interessant zijn. Als er te veel axioma’s zijn, kun je bijna alles bewijzen, en zou de wiskunde ook niet interessant zijn. Je kunt ook geen axioma’s hebben die elkaar tegenspreken.
Wiskunde gaat niet over het kiezen van de juiste set axioma’s, maar over het ontwikkelen van een raamwerk vanuit die uitgangspunten. Als je met andere axioma’s begint, krijg je een ander soort wiskunde, maar de logische argumenten zullen hetzelfde zijn. Elk gebied van de wiskunde heeft zijn eigen set van basisaxioma’s.
Wanneer wiskundigen een stelling bewezen hebben, publiceren ze die voor andere wiskundigen om te controleren. Soms vinden zij een fout in het logische argument, en soms wordt een fout pas vele jaren later gevonden. In principe is het echter altijd mogelijk om een bewijs op te splitsen in de basisaxioma’s.
Zettingstheorie en het Axioma van de Keuze

Om bewijzen te formuleren is het soms nodig om terug te gaan naar het fundament zelf van de taal waarin wiskunde wordt geschreven: de verzamelingenleer.
Een verzameling is een verzameling objecten, zoals getallen. De elementen van een verzameling worden meestal tussen gekrulde haakjes geschreven. We kunnen de unie van twee verzamelingen vinden (de verzameling van elementen die in een van beide verzamelingen zitten) of we kunnen de intersectie van twee verzamelingen vinden (de verzameling van elementen die in beide verzamelingen zitten).
Vele wiskundige problemen kunnen worden geformuleerd in de taal van de verzamelingenleer, en om ze te bewijzen hebben we verzamelingenleer axioma’s nodig. In de loop der tijd hebben wiskundigen verschillende verzamelingen axioma’s gebruikt, waarvan de negen Zermelo-Fraenkel (ZF) axioma’s de meest geaccepteerde zijn:
AXIOM OF EXTENSION
Als twee verzamelingen dezelfde elementen hebben, dan zijn ze gelijk.
AXIOM VAN UITBREIDING
We kunnen een deelverzameling vormen van een verzameling, die uit enkele elementen bestaat.

EENVOUDIG ZET AXIOM
Er is een verzameling zonder leden, geschreven als {} of ∅.
VOORZET AXIOM
Gegeven twee objecten x en y kunnen we een verzameling {x, y} vormen.
UNIE AXIOM
We kunnen de unie van twee of meer verzamelingen vormen.
POWER SET AXIOM
Gegeven aan een willekeurige verzameling, kunnen we de verzameling van alle deelverzamelingen vormen (de power set).
AXIOM VAN ONEINDIGHEID
Er is een verzameling met oneindig veel elementen.

AXIOM VAN DE GROND
Zetten zijn opgebouwd uit eenvoudiger verzamelingen, wat betekent dat elke (niet-lege) verzameling een minimaal lid heeft.
AXIOM VAN VERVANGING
Als we een functie toepassen op elk element in een verzameling, is het antwoord nog steeds een verzameling.
Als je nadenkt over verzamelingenleer, zullen de meeste van deze axioma’s volkomen voor de hand liggen – en dat is wat axioma’s horen te zijn. Er is echter een tiende axioma dat wat problematischer is:
AXIOM VAN KEUZE
Gegeven oneindig veel niet-lege verzamelingen, kun je uit elk van deze verzamelingen een element kiezen.
Op het eerste gezicht lijkt het Axioma van Keuze (AC) net zo onschuldig als de andere hierboven. Maar het gebruik van oneindigheid heeft een aantal onverwachte gevolgen. Je kunt AC bijvoorbeeld gebruiken om te bewijzen dat het mogelijk is een bol in vijf stukken te snijden en die weer in elkaar te zetten om twee bollen te maken, elk identiek aan de oorspronkelijke bol. Dit is slechts een theoretisch concept – de vereiste sneden zijn fractal, wat betekent dat ze in het echt niet kunnen bestaan, en sommige van de stukken zijn “niet-meetbaar”, wat betekent dat ze geen gedefinieerd volume hebben. Maar het feit dat het Axioma van Keuze kan worden gebruikt om deze onmogelijke sneden te construeren is nogal verontrustend.
Er is een hartstochtelijk debat onder logici gaande over het al dan niet aanvaarden van het axioma van keuze. Elke verzameling axioma’s vormt een kleine “wiskundige wereld”, en in verschillende werelden kunnen verschillende stellingen waar zijn. Het is eigenlijk maar de vraag of je gelukkig bent in een wereld te leven waar je van één bol twee bollen kunt maken…
Bewijs door Inductie
Bewijs door Inductie is een techniek die gebruikt kan worden om te bewijzen dat een bepaalde uitspraak waar is voor alle natuurlijke getallen 1, 2, 3, … De “uitspraak” is meestal een vergelijking of formule die een variabele n bevat die elk natuurlijk getal kan zijn. Laten we de uitspraak toegepast op n aanduiden met S(n). Dit zijn de vier stappen van wiskundige inductie:
- Eerst bewijzen we dat S(1) waar is, d.w.z. dat de uitspraak S waar is voor 1.
- Nu nemen we aan dat S(k) waar is, d.w.z. dat de uitspraak S waar is voor een natuurlijk getal k.
- Uit deze aanname proberen we af te leiden dat S(k + 1) ook waar is. Dus als S waar is voor één getal, is het ook waar voor het volgende getal.
- Omdat we weten dat S(1) waar is, moet S(2) ook waar zijn. En daarom moet S(3) waar zijn. En daarom moet S(4) waar zijn. En zo verder: S moet waar zijn voor alle getallen.

Inductie kan vergeleken worden met vallende dominostenen: als er een dominosteen valt, valt de volgende ook. De eerste stap, het bewijzen dat S(1) waar is, brengt de oneindige kettingreactie op gang.
De eerste stap wordt vaak over het hoofd gezien, omdat hij zo eenvoudig is. In feite is hij heel belangrijk en de hele inductieketen hangt ervan af – zoals enkele van de volgende voorbeelden zullen aantonen…
Het doel van het spel Towers of Hanoi is om een aantal schijven van de ene pin naar de andere te verplaatsen. Je mag maar één schijf per keer verplaatsen, en je mag geen grotere schijf bovenop een kleinere zetten. Probeer de toren van schijven van de eerste pin naar de laatste pin te verplaatsen, met zo min mogelijk zetten:
Aantal schijven: Start Over Bewegingen: 0
Nadat we de regels van het spel hebben begrepen, kunnen we proberen het minst aantal stappen te vinden dat nodig is, gegeven een willekeurig aantal schijven. Als we met het bovenstaande spel spelen, kunnen we vaststellen dat we met n schijven minstens 2n – 1 stappen nodig hebben. Laten we deze bewering S(n) noemen.
S(1) is duidelijk waar, want met slechts één schijf heb je maar één zet nodig, en 21 – 1 = 1.
Nemen we nu aan dat S(k) waar is, d.w.z. dat je 2k – 1 stappen nodig hebt voor k schijven. Als we dan k + 1 schijven hebben:
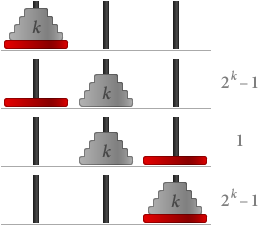
In totaal hebben we (2k – 1) + 1 + (2k – 1) = 2(k+1) – 1 stappen nodig. Dit betekent dat S(k + 1) ook waar is.
Met wiskundige inductie is S(n) waar voor alle waarden van n, wat betekent dat de meest efficiënte manier om n = V.Hanoi-schijven te verplaatsen 2n – 1 = Math.pow(2,V.Hanoi)-1 stappen vergt. ■
Laten we inductie gebruiken om te bewijzen dat de som van de eerste n natuurlijke getallen n (n + 1)2 is. We controleren eerst de vergelijking voor kleine waarden van n:
1 = 1 (1 + 1)2.
1 + 2 = 2 (2 + 1)2 = 3.
Nu nemen we aan dat het resultaat waar is voor k, dus dat 1 + 2 + … + k = k (k + 1)2, waarbij k een getal is dat we niet specificeren. Nu
1 + 2 + … + k + (k + 1) = k (k + 1)2 + (k + 1) = (k + 1) (k + 2)2 = (k + 1) 2.
We hebben zojuist bewezen dat als de vergelijking waar is voor een bepaalde k, zij ook waar is voor k + 1. Door wiskundige inductie is de vergelijking waar voor alle waarden van n. ■
Er is nog een andere slimme manier om bovenstaande vergelijking te bewijzen, die geen gebruik maakt van inductie. Naar verluidt ontdekte Carl Friedrich Gauss (1777 – 1855), een van de grootste wiskundigen uit de geschiedenis, deze methode op de lagere school, toen zijn leraar hem vroeg alle gehele getallen van 1 tot 100 bij elkaar op te tellen.
Met behulp van inductie willen we bewijzen dat alle mensen dezelfde haarkleur hebben. Laat S(n) de bewering zijn dat “elke groep van n mensen dezelfde haarkleur heeft”.
Het is duidelijk dat S(1) waar is: in elke groep van slechts één heeft iedereen dezelfde haarkleur.
Nu veronderstellen we S(k), dat in elke groep van k iedereen dezelfde haarkleur heeft. Als we iemand in de groep vervangen door iemand anders, vormen ze nog steeds een totaal van k en hebben ze dus dezelfde haarkleur. Dit werkt voor elke begingroep van mensen, wat betekent dat elke groep van k + 1 ook dezelfde haarkleur heeft. Daarom is S(k + 1) waar.
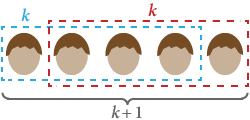
Met wiskundige inductie hebben alle mensen dezelfde haarkleur!
Er moet duidelijk iets mis zijn gegaan in bovenstaand bewijs – niet iedereen heeft immers dezelfde haarkleur. Kunt u de fout vinden?
Sommige stellingen kunnen niet helemaal worden bewezen met inductie – we moeten een enigszins aangepaste versie gebruiken die Sterke Inductie wordt genoemd. In plaats van S(k) aan te nemen om S(k + 1) te bewijzen, nemen we alle S(1), S(2), … S(k) aan om S(k + 1) te bewijzen. Alles wat met (zwakke) inductie bewezen kan worden, kan uiteraard ook met sterke inductie bewezen worden, maar niet omgekeerd.
De Fundamentele Stelling van de Rekenkunde stelt dat elk geheel getal groter dan 1 óf een priemgetal is, óf dat het op een in wezen unieke manier geschreven kan worden als het product van priemgetallen.
We kunnen delen ervan bewijzen met behulp van sterke inductie: laat S(n) de uitspraak zijn dat “het gehele getal n een priemgetal is of kan worden geschreven als het product van priemgetallen”. S(1) is een uitzondering, maar S(2) is duidelijk waar, want 2 is een priemgetal.
Nemen we nu aan dat S(1), S(2), …, S(k) allemaal waar zijn, voor een geheel getal k. We weten dat k + 1 ofwel een priemgetal is ofwel factoren kleiner dan k + 1 heeft. Door onze aanname weten we dat deze factoren geschreven kunnen worden als het product van priemgetallen. Tenzij het een priemgetal is, kan k + 1 dus ook geschreven worden als een product van priemgetallen. Dit betekent dat S(k + 1) waar is.
Door sterke inductie is S(n) waar voor alle getallen n groter dan 1. ■
Om te bewijzen dat deze priemfactorisatie uniek is (tenzij je verschillende volgordes van de factoren telt) is meer werk nodig, maar het is niet bijzonder moeilijk.
Het blijkt dat het principe van zwakke inductie en het principe van sterke inductie equivalent zijn: de een impliceert de ander. Ze zijn ook allebei equivalent met een derde stelling, het welordeningsprincipe: elke (niet-lege) verzameling van natuurlijke getallen heeft een minimaal element, kleiner dan alle andere.
Het welordeningsprincipe is de definiërende eigenschap van de natuurlijke getallen. Het is een van de basisaxioma’s die gebruikt worden om de natuurlijke getallen ![]() = {1, 2, 3, …} te definiëren. Deze axioma’s worden de Peano-axioma’s genoemd, genoemd naar de Italiaanse wiskundige Guiseppe Peano (1858 – 1932).
= {1, 2, 3, …} te definiëren. Deze axioma’s worden de Peano-axioma’s genoemd, genoemd naar de Italiaanse wiskundige Guiseppe Peano (1858 – 1932).
Proof by Contradiction
Proof by Contradiction is een andere belangrijke bewijstechniek. Als we een bewering S willen bewijzen, nemen we aan dat S niet waar is. Met deze aanname proberen we een vals resultaat af te leiden, zoals 0 = 1. Als al onze stappen juist waren en het resultaat is vals, dan moet onze eerste aanname fout zijn geweest. Onze eerste aanname was dat S niet waar is, wat betekent dat S eigenlijk waar is.
Deze techniek kan in veel verschillende omstandigheden worden gebruikt, zoals bewijzen dat √2 irrationeel is, bewijzen dat de reële getallen niet telbaar zijn, of bewijzen dat er oneindig veel priemgetallen zijn.
Hier volgt nog een leuk voorbeeld:
We kunnen bewijzen door middel van tegenspraak, samen met het goed-ordeningsprincipe, gebruiken om te bewijzen dat alle natuurlijke getallen “interessant” zijn.
Voorstel dat niet alle natuurlijke getallen interessant zijn, en laat S de verzameling van niet-interessante getallen zijn. Door het ordeningsprincipe van de put heeft S een kleinste lid x dat het kleinste niet-interessante getal is. Deze merkwaardige eigenschap maakt x duidelijk tot een bijzonder interessant getal. Dit is een tegenspraak omdat we aannamen dat x oninteressant was.
Daarom zijn alle getallen interessant. ■
Gödel en onbewijsbare stellingen

Kurt Gödel (1906-1978)
In het begin van de 20e eeuw begon de wiskunde snel te groeien, met duizenden wiskundigen die op talloze nieuwe gebieden werkten. David Hilbert (1862 – 1943) zette een uitgebreid programma op om de wiskunde te formaliseren en om alle inconsistenties in de grondslagen van de wiskunde op te lossen. Dit omvatte het bewijzen van alle stellingen met behulp van een stel eenvoudige en universele axioma’s, het bewijzen dat dit stel axioma’s consistent is, en het bewijzen dat dit stel axioma’s volledig is, d.w.z. dat elke wiskundige uitspraak bewezen of weerlegd kan worden met behulp van de axioma’s.
Helaas werden deze plannen teniet gedaan door Kurt Gödel in 1931. Hij bewees dat in elk (voldoende complex) wiskundig systeem met een bepaalde verzameling axioma’s, uitspraken te vinden zijn die met behulp van die axioma’s noch bewezen, noch weerlegd kunnen worden. Het is ook niet mogelijk om te bewijzen dat een bepaalde verzameling axioma’s consistent is, met niets anders dan de axioma’s zelf.
Gödel’s ontdekking is gebaseerd op het feit dat een verzameling axioma’s niet gebruikt kan worden om iets over zichzelf te zeggen, zoals of ze consistent is. Problemen met zelfverwijzing doen zich niet alleen in de wiskunde voor, maar ook in de taal. Hier is de leugenaarsparadox:
“Deze zin is onwaar.”
De zin hierboven probeert iets over zichzelf te zeggen. Als hij waar is, zegt de zin dat hij onwaar is. Als de zin onwaar is, dan zegt de zin ons dat hij niet onwaar is, dat wil zeggen dat hij waar is. In feite is de zin noch waar, noch onwaar.
Toen Gödel’s stellingen voor het eerst gepubliceerd werden, waren ze voor veel wiskundigen zeer verontrustend. Als je een waarneming wilt bewijzen, weet je niet of er een bewijs bestaat – het resultaat kan waar zijn, maar onbewijsbaar. Tegenwoordig weten we dat onvolledigheid een fundamenteel onderdeel is van niet alleen de logica, maar ook van de informatica, die berust op machines die logische bewerkingen uitvoeren.
Verrassend genoeg is het mogelijk te bewijzen dat bepaalde stellingen onbewijsbaar zijn. Een voorbeeld is de Continuüm Hypothese, die gaat over de grootte van oneindige verzamelingen.
Tegen het einde van zijn leven kreeg Kurt Gödel ernstige psychische problemen en hij stierf in 1978 aan zelfdoding. Zijn inzichten in de grondslagen van de logica waren de meest diepgaande sinds de ontwikkeling van het bewijs door de oude Grieken.