
Bertrand Russell (1872-1970) en A.N. Whitehead (1861-1947)
Bertrand Russell en Alfred North Whitehead waren Britse wiskundigen, logici en filosofen, die in de voorhoede stonden van de Britse opstand tegen het continentale idealisme in het begin van de 20e eeuw en die samen belangrijke bijdragen leverden op het gebied van de wiskundige logica en de verzamelingenleer.
Whitehead was de oudste van de twee en kwam uit een meer zuivere wiskunde achtergrond. Hij werd Russells leraar aan het Trinity College in Cambridge in de jaren 1890, en werkte vervolgens met zijn meer gevierde ex-leerling in het eerste decennium van de 20e eeuw samen aan hun monumentale werk, de “Principia Mathematica”. Na de Eerste Wereldoorlog, waarvan Russell een groot deel van de tijd in de gevangenis doorbracht vanwege zijn pacifistische activiteiten, liep de samenwerking echter spaak en bleef Whiteheads academische carrière in de schaduw van die van de meer flamboyante Russell. Hij emigreerde in de jaren twintig naar de Verenigde Staten, en bracht daar de rest van zijn leven door.
Russell werd geboren in een welgestelde familie van de Britse aristocratie, hoewel zijn ouders voor die tijd uiterst liberaal en radicaal waren. Zijn ouders stierven toen Russell nog vrij jong was en hij werd grotendeels opgevoed door zijn overtuigd Victoriaanse (hoewel vrij progressieve) grootmoeder. Zijn adolescentie was zeer eenzaam en hij leed aan periodes van depressie, later beweren dat het was alleen zijn liefde voor de wiskunde dat hield hem van zelfmoord. Hij studeerde wiskunde en filosofie aan de Universiteit van Cambridge bij G.E. Moore en A.N. Whitehead, waar hij zich ontwikkelde tot een vernieuwend filosoof, een productief schrijver over vele onderwerpen, een overtuigd atheïst en een bevlogen wiskundige en logicus. Tegenwoordig wordt hij beschouwd als een van de grondleggers van de analytische filosofie, maar hij schreef over bijna elk belangrijk gebied van de filosofie, met name de metafysica, de ethiek, de epistemologie, de filosofie van de wiskunde en de taalfilosofie.
Russell was gedurende zijn lange leven een toegewijd en spraakmakend politiek activist. Hij was een prominente anti-oorlogsactivist tijdens zowel de Eerste als de Tweede Wereldoorlog, was een voorvechter van vrije handel en anti-imperialisme, en werd later een felle campagnevoerder voor nucleaire ontwapening en socialisme, en tegen Adolf Hitler, het totalitarisme van de Sovjet-Unie en de betrokkenheid van de VS bij de oorlog in Vietnam.
Russells Paradox
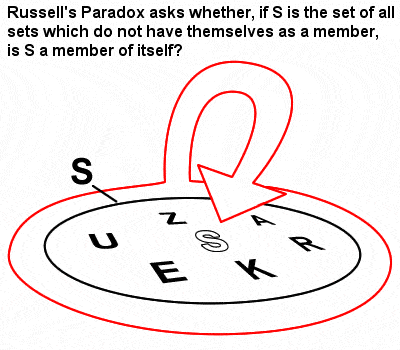
Russells Paradox
Russells wiskunde werd sterk beïnvloed door de verzamelingenleer en de logica die Gottlob Frege had ontwikkeld in het kielzog van het baanbrekende vroege werk van Cantor over verzamelingen. In zijn “The Principles of Mathematics” uit 1903 identificeerde hij echter wat bekend is geworden als de Paradox van Russell (een verzameling die verzamelingen bevat die geen leden van zichzelf zijn), die aantoonde dat Frege’s naïeve verzamelingenleer in feite tot tegenstrijdigheden kon leiden.
De paradox wordt soms geïllustreerd met dit simplistische voorbeeld: “Als een barbier alle en alleen die mannen in het dorp scheert die zichzelf niet scheren, scheert hij dan zichzelf?”
De paradox leek te impliceren dat de grondslagen van de hele wiskunde niet meer te vertrouwen waren, en dat, zelfs in de wiskunde, de waarheid nooit absoluut gekend kon worden (Gödel’s en Turing’s latere werk zouden dit alleen maar erger maken). De kritiek van Russell was voldoende om Frege’s vertrouwen in het hele bouwwerk van de logica aan het wankelen te brengen, en hij was genadig genoeg om dit openlijk toe te geven in een haastig geschreven appendix bij Deel II van zijn “Basiswetten van de Rekenkunde”.
Maar Russell’s magnum opus was het monolithische “Principia Mathematica”, gepubliceerd in drie delen in 1910, 1912 en 1913. Het eerste deel werd mede geschreven door Whitehead, hoewel de latere twee delen bijna volledig Russell’s werk waren. De ambitie van dit ambitieuze werk was niets minder dan een poging om de hele wiskunde af te leiden uit zuiver logische axioma’s, en daarbij het soort paradoxen en tegenstrijdigheden te vermijden die in Frege’s eerdere werk over de verzamelingenleer voorkwamen. Russell bereikte dit door gebruik te maken van een theorie of systeem van “typen”, waarbij elke wiskundige entiteit wordt toegewezen aan een type binnen een hiërarchie van typen, zodat objecten van een bepaald type uitsluitend worden opgebouwd uit objecten van voorgaande typen lager in de hiërarchie, waardoor lussen worden voorkomen. Elke verzameling van elementen is dus van een ander type dan elk van zijn elementen, zodat men niet kan spreken van de “verzameling van alle verzamelingen” en soortgelijke constructies, die tot paradoxen leiden.
De “Principia” vereiste echter, naast de basisaxioma’s van de typentheorie, nog drie axioma’s die niet waar leken te zijn als louter logische kwesties, namelijk het “axioma van oneindigheid” (dat het bestaan van ten minste één oneindige verzameling garandeert, namelijk de verzameling van alle natuurlijke getallen), het “axioma van keuze” (dat verzekert dat, gegeven een verzameling van “bakken” die elk ten minste één voorwerp bevatten, het mogelijk is om uit elke bak precies één voorwerp te kiezen, zelfs als er oneindig veel bakken zijn, en dat er geen “regel” is voor welk voorwerp uit elke bak gekozen moet worden) en Russells eigen “axioma van reduceerbaarheid” (dat stelt dat elke propositionele waarheidsfunctie kan worden uitgedrukt door een formeel equivalente predicatieve waarheidsfunctie).
Tijdens de ongeveer tien jaar dat Russell en Whitehead aan de “Principia” werkten, werd ontwerp na ontwerp begonnen en weer verlaten, omdat Russell voortdurend zijn uitgangspunten heroverwoog. Russell en zijn vrouw Alys trokken zelfs bij de Whiteheads in om het werk te bespoedigen, hoewel zijn eigen huwelijk eronder leed toen Russell verliefd werd op Whiteheads jonge vrouw, Evelyn. Uiteindelijk drong Whitehead aan op publicatie van het werk, ook al was het niet (en zou het nooit) volledig zijn, hoewel zij gedwongen waren het op eigen kosten uit te geven omdat geen enkele commerciële uitgever het wilde aanraken.
Principia Mathematica

Een klein deel van het lange bewijs dat 1+1 =2 in de “Principia Mathematica”
Enig idee van de omvang en uitgebreidheid van de “Principia” kan worden afgeleid uit het feit dat het meer dan 360 pagina’s kost om definitief te bewijzen dat 1 + 1 = 2.
Heden ten dage wordt het algemeen beschouwd als een van de belangrijkste en meest baanbrekende werken in de logica sinds Aristoteles’ “Organon”. Het leek opmerkelijk succesvol en veerkrachtig in zijn ambitieuze doelstellingen, en verwierf spoedig wereldfaam voor Russell en Whitehead. Het was immers pas Gödel’s onvolledigheidstheorema uit 1931 dat uiteindelijk aantoonde dat de “Principia” niet zowel consistent als volledig kon zijn.
Russell werd in 1949 onderscheiden met de Orde van Verdienste en in het jaar daarop met de Nobelprijs voor de Literatuur. Zijn faam bleef groeien, ook buiten academische kringen, en hij werd op latere leeftijd een soort begrip, zij het grotendeels als gevolg van zijn filosofische bijdragen en zijn politieke en sociale activisme, dat hij tot het einde van zijn lange leven voortzette. Hij stierf aan griep in zijn geliefde Wales op de hoge leeftijd van 97 jaar.
| << Terug naar Hardy en Ramanujan | Voorwaarts naar Hilbert >> |