Blokdiagrammen bestaan uit een enkel blok of een combinatie van blokken. Deze worden gebruikt om de regelsystemen in picturale vorm weer te geven.
Basiselementen van blokdiagram
De basiselementen van een blokdiagram zijn een blok, het sommatiepunt en het startpunt. Laten we het blokschema van een gesloten-lusbesturingssysteem beschouwen zoals weergegeven in de volgende figuur om deze elementen te identificeren.
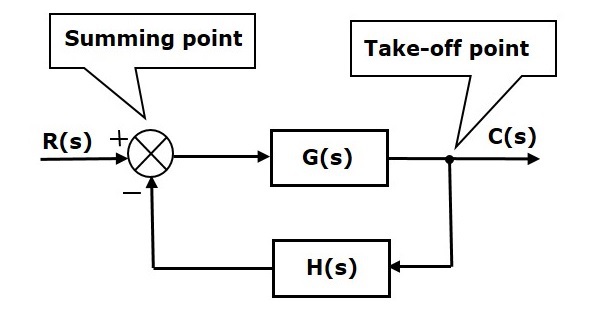
Het bovenstaande blokschema bestaat uit twee blokken met overdrachtsfuncties G(s) en H(s). Het heeft ook een sommeringspunt en een startpunt. Pijlen geven de richting van de signaalstroom aan. Laten we deze elementen nu één voor één bespreken.
Blok
De overdrachtsfunctie van een component wordt voorgesteld door een blok. Een blok heeft één ingang en één uitgang.
De volgende figuur toont een blok met ingang X(s), uitgang Y(s) en de overdrachtsfunctie G(s).

Transferfunctie,$G(s)=\frac{Y(s)}{X(s)}$
$$\Rightarrow Y(s)=G(s)X(s)$$
De output van het blok wordt verkregen door de transferfunctie van het blok te vermenigvuldigen met de input.
Sommatiepunt
Het sommeringspunt wordt voorgesteld met een cirkel met een kruis (X) erin. Het heeft twee of meer ingangen en één uitgang. Het produceert de algebraïsche som van de ingangen. Het voert ook de optelling of aftrekking uit of een combinatie van optelling en aftrekking van de ingangen op basis van de polariteit van de ingangen. Laten we deze drie bewerkingen één voor één bekijken.
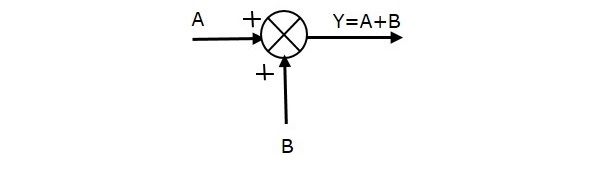
De volgende figuur toont het sommeringspunt met twee ingangen (A, B) en één uitgang (Y). Hier hebben de ingangen A en B een positief teken. Het sommeringspunt produceert dus de uitgang Y als som van A en B.
i.e.,Y = A + B.
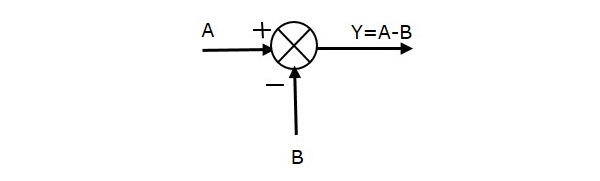
De volgende figuur toont het sommeringspunt met twee ingangen (A, B) en één uitgang (Y). Hier hebben de ingangen A en B tegengestelde tekens, d.w.z. A heeft een positief teken en B heeft een negatief teken. Het sommeringspunt produceert dus de uitgang Y als het verschil van A en B.
Y = A + (-B) = A – B.
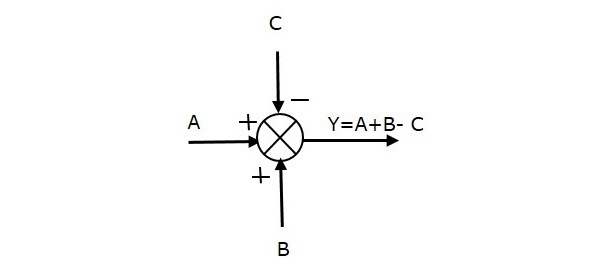
De volgende figuur toont het sommeringspunt met drie ingangen (A, B, C) en één uitgang (Y). Hier hebben de ingangen A en B een positief teken en C een negatief teken. Het sommeringspunt produceert dus de uitgang Y als
Y = A + B + (-C) = A + B – C.
Take-off-punt
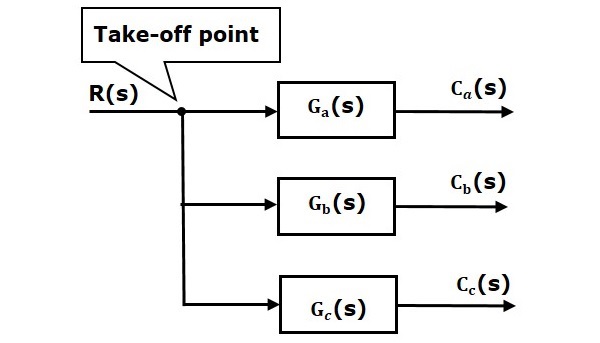
Het take-off-punt is een punt van waaruit hetzelfde ingangssignaal door meer dan één tak kan worden geleid. Dat betekent dat we met behulp van een aftakpunt dezelfde ingang kunnen toepassen op een of meer blokken, sommatiepunten.
In de volgende figuur wordt het aftakpunt gebruikt om dezelfde ingang, R(s), te verbinden met nog twee blokken.
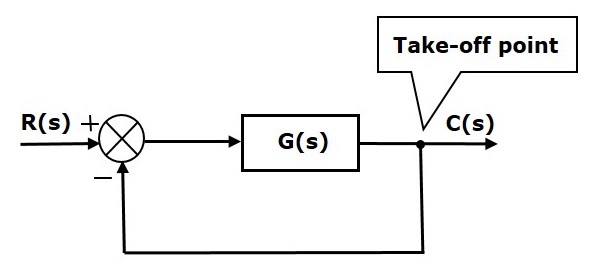
In de volgende figuur wordt het aftakpunt gebruikt om de uitgang C(s), als een van de ingangen, met het sommeringspunt te verbinden.
Blokdiagram Weergave van Elektrische Systemen
In dit gedeelte laten we een elektrisch systeem met een blokdiagram weergeven. Elektrische systemen bevatten hoofdzakelijk drie basiselementen – weerstand, spoel en condensator.
Beschouw een serie RLC-schakeling zoals weergegeven in de volgende figuur. Waar Vi(t) en Vo(t) de ingangs- en uitgangsspanningen zijn. Laat i(t) de stroom zijn die door de schakeling loopt. Deze schakeling bevindt zich in het tijdsdomein.
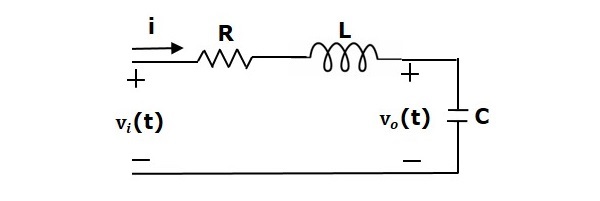
Door de Laplace-transformatie op deze schakeling toe te passen, krijgt u de schakeling in het s-domein. De schakeling is zoals weergegeven in de volgende figuur.
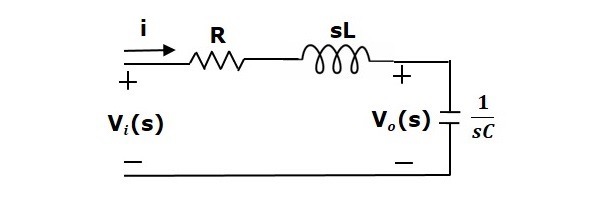
Vanuit de bovenstaande schakeling kunnen we schrijven
$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$
$Rechterpijl I(s)= links {\frac{1}{R+sL} \links \{ V_i(s)-V_o(s) rechts \}$ (Vergelijking 1)
$V_o(s)=links ( \frac{1}{sC} \rechts )I(s)$ (Vergelijking 2)
Laten we nu de blokschema’s voor deze twee vergelijkingen afzonderlijk tekenen. En vervolgens deze blokdiagrammen op de juiste wijze combineren om het totale blokdiagram van serie RLC Circuit (s-domein) te krijgen.
Vergelijking 1 kan worden geïmplementeerd met een blok met de overdrachtsfunctie, $\frac{1}{R+sL}$. De in- en uitgang van dit blok zijn $ links \{ V_i(s)-V_o(s) \rechts \}$ en $I(s)$. We hebben een sommatiepunt nodig om $_left \{ V_i(s)-V_o(s) \right \}$ te krijgen. Het blokschema van vergelijking 1 is weergegeven in de volgende figuur.
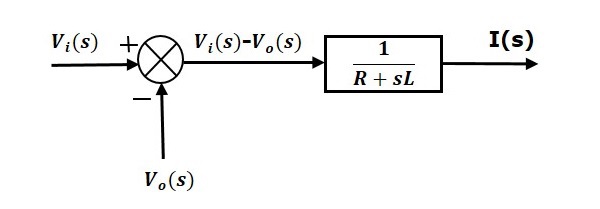
Vergelijking 2 kan worden geïmplementeerd met een blok dat een overdrachtsfunctie heeft, $\frac{1}{sC}$. De in- en uitgang van dit blok zijn $I(s)$ en $V_o(s)$. Het blokschema van vergelijking 2 is weergegeven in de volgende figuur.
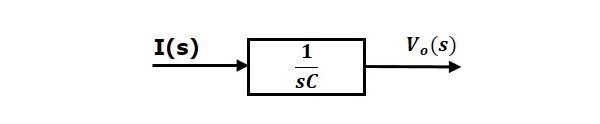
Het algemene blokschema van de reeks van RLC Circuit (s-domein) is weergegeven in de volgende figuur.
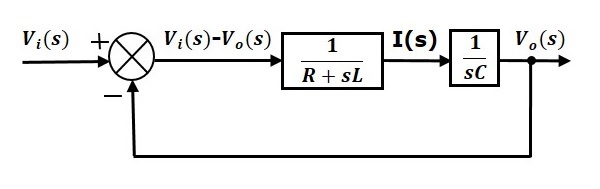
Op dezelfde manier kunt u het blokschema van elk elektrisch circuit of systeem tekenen door gewoon deze eenvoudige procedure te volgen.
-
Verander het tijdsdomein elektrische circuit in een s-domein elektrisch circuit door Laplace transform toe te passen.
-
Schrijf de vergelijkingen op voor de stroom door alle elementen van de serietakken en de spanning over alle shunttakken.
-
Teken de blokdiagrammen voor alle bovenstaande vergelijkingen afzonderlijk.
-
Combineer al deze blokschema’s op de juiste wijze om het totale blokschema van de elektrische schakeling (s-domein) te verkrijgen.