Chemguide: Support for CIE A level Chemistry
Leerresultaat 11.2(f)
Deze verklaring gaat over verdelingscoëfficiënten.
Voordat je verder gaat, moet je de verklaring opzoeken en lezen in je exemplaar van de syllabus.
Deelcoëfficiënten
Als je twee onvermengbare vloeistoffen hebt, zoals ether en water, en je schudt ze in een scheitrechter, dan vormen ze natuurlijk twee lagen. De ether heeft een geringere dichtheid dan het water, en vormt dus de bovenste laag.
Nu veronderstel dat je een mengsel van ether en water schudt dat een stof bevat die in beide oplosbaar is. Stel dat de stof, X, beter oplosbaar is in ether dan in water.
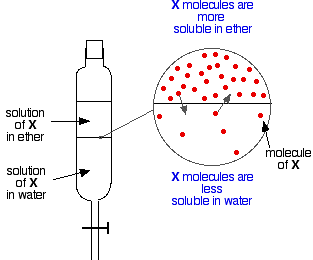
Deeltjes X zullen de grens tussen de twee vloeistoflagen overschrijden, en je krijgt al snel een dynamisch evenwicht. Voor elk deeltje dat naar de bovenste laag beweegt, beweegt er een terug naar de onderste laag.
Je zou hier een vergelijking voor kunnen schrijven:
. . en net als bij elk ander evenwicht kun je een evenwichtsconstante vinden:
Deze evenwichtsconstante wordt de verdelingscoëfficiënt genoemd, en krijgt vaak het symbool Kpc.
Zoals andere evenwichtsconstanten zijn verdelingscoëfficiënten constant bij een constante temperatuur, maar ze hebben ook nog enkele andere beperkingen. Ze werken alleen goed voor tamelijk verdunde oplossingen, en de opgeloste stof moet in beide oplosmiddelen dezelfde chemische vorm hebben. Het mag niet reageren, of ioniseren of associëren (zich verenigen in dimeren, bijvoorbeeld).
Berekeningen van verdelingscoëfficiënten
Een opmerking over eenheden
Merk op dat de verdelingscoëfficiënt een eenvoudige verhouding van twee concentraties is. Het maakt niet uit welke concentratie-eenheden je gebruikt – als je boven en onder maar dezelfde gebruikt.
Je zou mol dm-3 kunnen gebruiken, maar vaker gebruik je g cm-3 – gram per kubieke centimeter.
Technisch gezien kunnen de vierkante haakjes alleen worden gebruikt voor concentratie in mol dm-3, maar het Application Support Booklet en de beoordelingsschema’s van CIE gebruiken het allebei ook voor andere eenheden.
Ik ben niet bereid dat te doen, en zal dus de term “concentratie van X” gebruiken in plaats van waar niet-standaardconcentratie-eenheden worden gebruikt.
Bereken een verdelingscoëfficiënt
Toen een oplossing van 1,00 g X in 100 cm3 water werd geschud met 10 cm3 ether, werd 0,80 g X overgebracht naar de etherlaag. Bereken de verdelingscoëfficiënt van X tussen ether en water.
Als je gevraagd wordt een verdelingscoëfficiënt tussen twee oplosmiddelen te berekenen, gaat de concentratie van het eerst genoemde oplosmiddel boven op de Kpc-uitdrukking. Dus in dit geval:
U hebt genoeg informatie om beide concentraties in g cm-3 te berekenen.
concentratie van X in ether = 0,80/10 g cm-3
Als 0,80 g in de ether werd overgebracht, bleef er 1,00 – 0,80 g = 0,00 – 0,80 g in het water over.
Als 0,80 g in de ether werd overgebracht, bleef er 1,00 – 0,80 g = 0,00 – 0,80 g in het water over.20 g in het water achterblijven.
concentratie van X in water = 0,20/100 g cm-3
Dus:
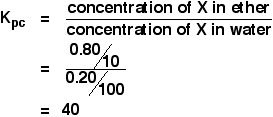
Het spreekt vanzelf dat je de concentraties in ether en in water als reële getallen zou kunnen uitwerken voordat je ze in de uitdrukking zet. Doe het zoals jij je het prettigst voelt.
Zulke verdelingscoëfficiënten hebben geen eenheden – de eenheden vallen weg omdat ze boven en onder hetzelfde zijn.
Berekeningen met verdelingscoëfficiënten
In de CIE syllabus staat specifiek dat je een verdelingscoëfficiënt moet kunnen berekenen (met andere woorden, wat wij zojuist hebben gedaan). Er staat helemaal niets in over het gebruik ervan om andere dingen te berekenen. Deze extra berekeningen worden besproken in het Application Support Booklet en zijn twee keer gevraagd in examens tot juni 2013 (beide in 2009).
Het cursusboek bevat ze niet (heel juist!) omdat de syllabus ze niet noemt, en dit boek is door CIE-examinatoren bekrachtigd als een “volledige en nauwkeurige dekking” van de syllabus. Betekent dit dat CIE in de toekomst geen vragen meer zal stellen? Reken er niet op!
Een basisvoorbeeld
We zullen hetzelfde geval gebruiken als voorheen – dezelfde oplosmiddelen, dezelfde X en dezelfde verdelingscoëfficiënt die we zojuist hebben berekend.
Dit keer gaan we uitrekenen hoeveel er in de etherlaag zou zijn terechtgekomen als we de oorspronkelijke oplossing van 1,00 g X in 100 cm3 water hadden geschud met slechts 5 cm3 ether.
We proberen de massa van het geëxtraheerde X te berekenen. Laten we dat m noemen.
Werk nu een uitdrukking uit voor de concentratie van de oplossing van X in ether.
concentratie van X in ether = m/5 g cm-3
Hoe zit het met het water? Er blijft (1,00 – m) g X in het water over. Dus:
concentratie van X in water = (1,00 – m)/100 g cm-3
Nu kun je dit alles in de uitdrukking van de verdelingscoëfficiënt zetten. Bedenk dat we de verdelingscoëfficiënt van X tussen ether en water al hebben berekend op 40.
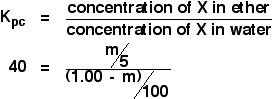
U staat dan alleen nog voor een eenvoudig, maar ietwat vervelend stukje algebra:
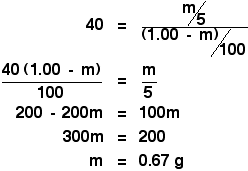
Maken we het nog vervelender!
In de oorspronkelijke berekening om de verdelingscoëfficiënt te vinden, werd u verteld dat als u de oorspronkelijke oplossing van 1,00 g X in 100 cm3 water met 10 cm3 ether schudde, u 0,80 g X extraheerde.
Door te schudden met 5 cm3 ether, hebben we zojuist uitgerekend dat u 0,67 g X zou extraheren.
Dat zou 0,33 g X achterlaten in de 100 cm3 water. Stel dat je deze oplossing zorgvuldig had bewaard, en daarna had geschud met een tweede verse 5 cm3 ether.
Hoeveel van X zou je er in totaal uithalen door de ether als twee afzonderlijke partijen van 5 cm3 te gebruiken in plaats van de 10 cm3 in één keer?
Laten we de massa van X die met de tweede partij ether wordt gewonnen n noemen – zodat we niet in de war raken.
Werk een uitdrukking uit voor de concentratie van de oplossing van X in ether.
concentratie van X in ether = n/5 g cm-3
Hoe zit het met het water? Na de tweede extractie zal er (0,33 – n) g X in het water overblijven. Dus:
concentratie van X in water = (0,33 – n)/100 g cm-3
Nu kunt u dit alles in de uitdrukking van de verdelingscoëfficiënt voor X tussen ether en water zetten zoals voorheen.
Dit betekent dat als je de twee partijen ether van 5 cm3 zou samenvoegen, je in totaal 0,67 + 0,22 g X zou hebben onttrokken. Dat is 0.89 g.
U werd oorspronkelijk verteld dat als u dit maar één keer had gedaan, met de ether als één enkele partij van 10 cm3, u slechts 0,80 g zou hebben geëxtraheerd.
U krijgt een efficiëntere extractie door uw oplosmiddel op te splitsen in kleinere volumes, zoals hierboven.
U gebruikt dit soort technieken bij de bereiding van sommige organische verbindingen. Je extraheert wat je probeert te maken uit een rommelige oplossing in water, zodat het in een organisch oplosmiddel terechtkomt. Vervolgens verwijder je het oplosmiddel door zorgvuldige destillatie.
CIE stelde in juni 2009 paper 4 Q8 een vraag die hier op leek. Je moest een waarde voor de verdelingscoëfficiënt berekenen en die vervolgens gebruiken in een extractie in twee stappen, precies zoals hierboven. De berekening was 4 punten waard. Dit kan vervelend zijn en (afgezien van het berekenen van de verdelingscoëfficiënt) niet in de syllabus staan, maar je kunt het je niet veroorloven het niet te kunnen doen.
