16.3 Gemengde strategieën
Leerdoel
- Welke spelen vereisen of staan randomisatie toe als deel van hun oplossing?
Laten we het matchen van centen nog eens bekijken, zoals geïllustreerd in Figuur 16.13 “Matching pennies again”.
Figuur 16.13 “Matching pennies again”
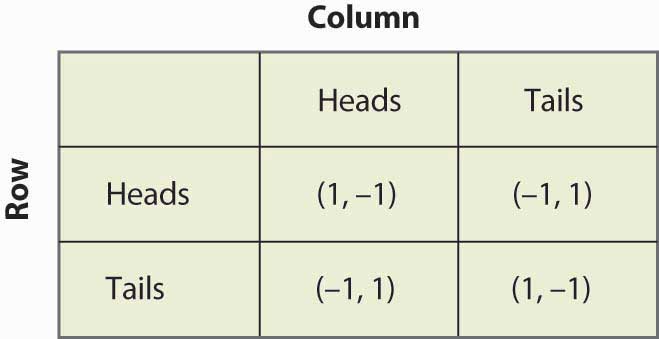
Voorstel dat Row gelooft dat Kolom Kop speelt met kans p. Als Row Kop speelt, krijgt Row 1 met kans p en -1 met kans (1 – p), voor een verwachte waarde van 2p – 1. Op dezelfde manier, als Rij munt speelt, krijgt Rij -1 met kans p (als Kolom Kop speelt), en 1 met kans (1 – p), voor een verwachte waarde van 1 – 2p. Dit is samengevat in figuur 16.14 “Mixed strategy in matching pennies”.
Als 2p – 1 > 1 – 2p, dan is Row gemiddeld beter af door Kop te spelen dan Munt. Evenzo, als 2p – 1 < 1 – 2p, dan is Row beter af met Kop dan munt. Als, aan de andere kant, 2p – 1 = 1 – 2p, dan krijgt Row dezelfde uitbetaling, ongeacht wat Row doet. In dit geval kan Row Kop spelen, Munt spelen, of een munt opgooien en Row’s spel randomiseren.
Een mixed strategy Nash-evenwichtEen Nash-evenwicht waarbij minstens één speler een gerandomiseerde strategie speelt en geen enkele speler zijn of haar verwachte uitbetaling kan verhogen door een alternatieve strategie te spelen. houdt in dat minstens één speler een gerandomiseerde strategie speelt en geen enkele speler zijn of haar verwachte uitbetaling kan verhogen door een alternatieve strategie te spelen. Een Nash-evenwicht waarin geen enkele speler willekeurig speelt, heet een zuiver strategie Nash-evenwichtEen Nash-evenwicht waarin geen enkele speler willekeurig speelt..
Figuur 16.14 Gemengde strategie bij het matchen van pennies
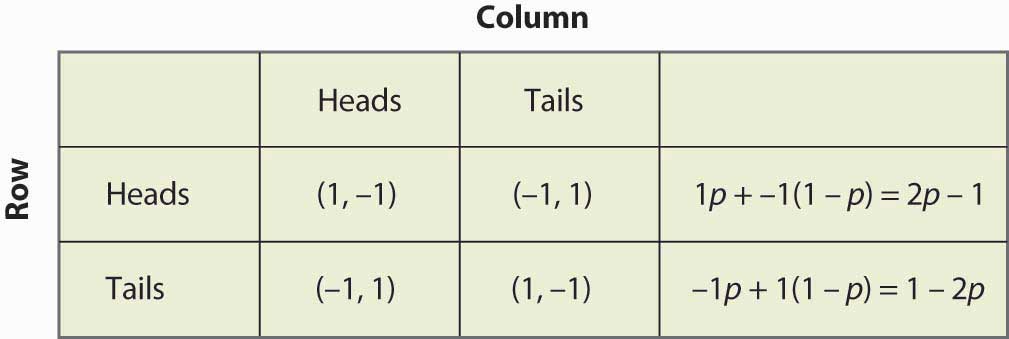
Merk op dat randomisatie gelijkheid van verwachte uitbetalingen vereist. Als een speler verondersteld wordt te randomiseren over strategie A of strategie B, dan moeten beide strategieën dezelfde verwachte uitbetaling opleveren. Anders zou de speler een van beide verkiezen en de andere niet spelen.
Het berekenen van een gemengde strategie heeft een element dat vaak verwarrend overkomt. Stel dat Row gaat randomiseren. Dan moeten Row’s uitbetalingen gelijk zijn voor alle strategieën die Row met positieve waarschijnlijkheid speelt. Maar die gelijkheid in Row’s uitbetalingen bepaalt niet de waarschijnlijkheden waarmee Row de verschillende rijen speelt. In plaats daarvan bepaalt de gelijkheid van Row’s uitbetalingen de waarschijnlijkheid waarmee Column de verschillende kolommen speelt. De reden hiervoor is dat het de kansen van de kolommen zijn die de verwachte uitbetalingen voor Row bepalen; als Row gaat randomiseren, dan moeten de kansen van de kolommen zodanig zijn dat Row bereid is te randomiseren.
Dus, bijvoorbeeld, we berekenden de uitbetaling aan Row van het spelen van Heads, dat was 2p – 1, waarbij p de kans was dat Column Heads speelde. Op dezelfde manier was de winst voor Rij om munt te spelen 1 – 2p. Row is bereid te randomiseren als deze kansen gelijk zijn, waardoor p = ½.
Nu gaan we een wat uitdagender voorbeeld proberen en de strijd tussen de seksen opnieuw bekijken. Figuur 16.15 “Mixed strategy in battle of the sexes” illustreert de uitbetalingen nog eens.
Figuur 16.15 Mixed strategy in battle of the sexes
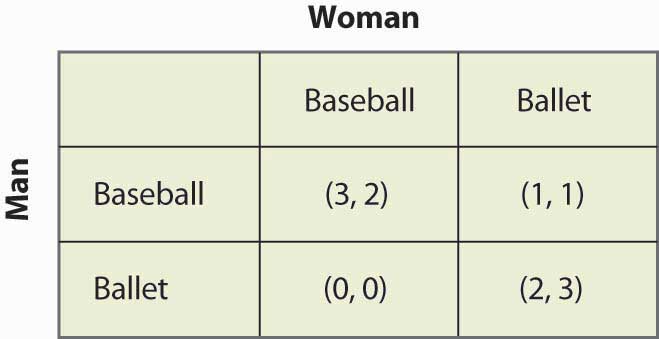
Dit spel heeft twee zuivere strategie Nash-evenwichten: (Honkbal, Honkbal) en (Ballet, Ballet). Is er een gemengde strategie? Om een gemengde strategie te berekenen, laat de Vrouw naar het Honkbalspel gaan met kans p, en de Man naar het Honkbalspel met kans q. Figuur 16.16 “Volledige berekening van de gemengde strategie” bevat de berekening van de gemengde strategie payoffs voor elke speler.
Figuur 16.16 Volledige berekening van de gemengde strategie
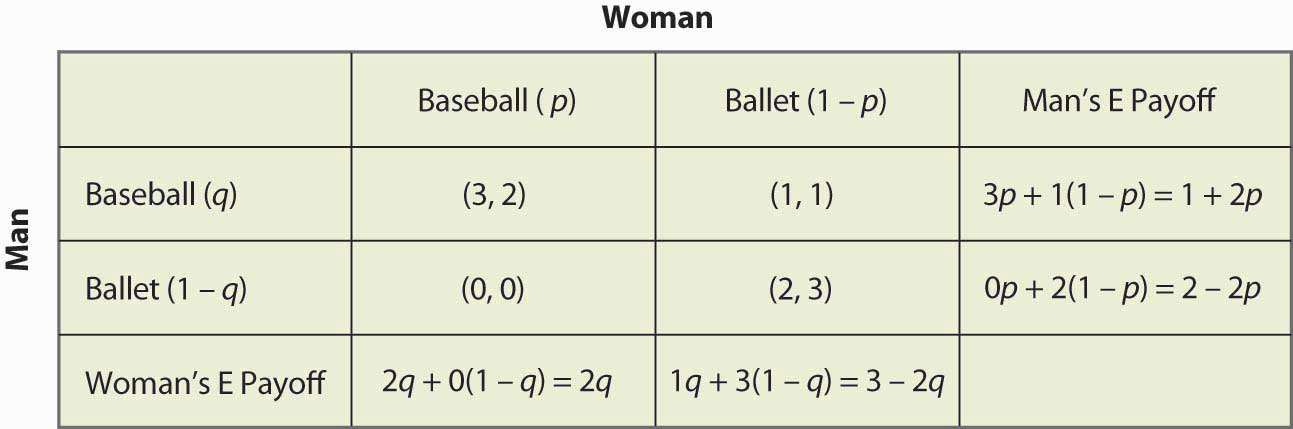
Bijv. als de Man (rij-speler) naar de Honkbalwedstrijd gaat, krijgt hij 3 als de Vrouw naar de Honkbalwedstrijd gaat (kans p), en anders krijgt hij 1, voor een verwachte uitbetaling van 3p + 1(1 – p) = 1 + 2p. De andere berekeningen zijn vergelijkbaar, maar je moet zeker de logica doorlopen en elke berekening verifiëren.
Een gemengde strategie in de strijd der seksen vereist dat beide partijen randomiseren (omdat een zuivere strategie van een van beide partijen randomisatie door de ander verhindert). De onverschilligheid van de man tussen naar het honkbalspel en naar het ballet gaan vereist 1 + 2p = 2 – 2p, hetgeen p = ¼ oplevert. Dat wil zeggen dat de man bereid zal zijn willekeurig te kiezen welk evenement hij bezoekt indien de vrouw ¾ van de tijd naar het ballet gaat, en anders naar de honkbalwedstrijd. Dit maakt de man onverschillig tussen de twee evenementen omdat hij liever bij de vrouw is, maar ook graag naar de honkbalwedstrijd gaat. Om het voordeel van de honkbalwedstrijd voor hem goed te maken, moet de vrouw vaker bij het ballet zijn.
Zo ook moet de vrouw, om te willekeurig te zijn, gelijke uitbetalingen krijgen als ze naar de honkbalwedstrijd gaat en als ze naar het ballet gaat, waarvoor 2q = 3 – 2q, of q = ¾ nodig is. De kans dat de Man naar de Honkbalwedstrijd gaat is dus ¾, en hij gaat ¼ van de tijd naar het Ballet. Dit zijn onafhankelijke kansen, dus om de kans te krijgen dat beiden naar de Honkbalwedstrijd gaan, vermenigvuldigen we de kansen, wat 3/16 oplevert. In figuur 16.17 “Mixed strategy probabilities” zijn de kansen voor alle vier de mogelijke uitkomsten ingevuld.
Figuur 16.17 Mixed strategy probabilities
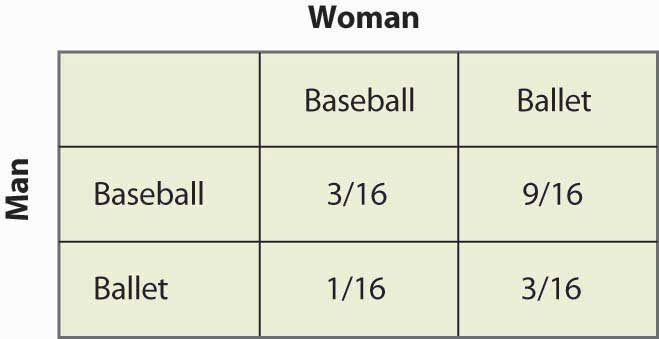
Merk op dat meer dan de helft van de tijd (Baseball, Ballet) de uitkomst is van de mixed strategy en de twee personen niet samen zijn. Dit gebrek aan coördinatie is in het algemeen een kenmerk van gemengde strategie-evenwichten. De verwachte uitbetalingen voor beide spelers zijn ook gemakkelijk te berekenen. Het loon van de man is 1 + 2p = 2 – 2p, en aangezien p = ¼, krijgt de man 1½. Een gelijkaardige berekening toont aan dat het loon van de vrouw hetzelfde is. Beiden doen het dus slechter dan het coördineren van hun minder gewenste uitkomst. Maar dit gemengde strategie Nash-evenwicht, hoe onwenselijk het ook lijkt, is een Nash-evenwicht in die zin dat geen van beide partijen zijn of haar eigen beloning kan verbeteren, gegeven het gedrag van de andere partij.
In de strijd tussen de seksen kan het gemengde strategie Nash-evenwicht onwaarschijnlijk lijken; en we zouden verwachten dat het paar effectiever zou coördineren. Een eenvoudig telefoongesprek zou de gemengde strategie inderdaad moeten uitsluiten. Laten we eens kijken naar een ander spel dat verband houdt met de strijd tussen de seksen, waar een gebrek aan coördinatie logischer is. Dit is het spel “kip”. Bij dit spel rijden twee spelers naar elkaar toe, in een poging de ander te overtuigen voor te wijken en uiteindelijk uit te wijken in een greppel. Als beiden in de greppel uitwijken, noemen we de uitkomst gelijkspel en krijgen beiden nul. Als de ene bestuurder uitwijkt en de andere niet, verliest de bestuurder die uitwijkt en wint de andere bestuurder, en geven we de winnaar een punt. Merk op dat het toevoegen van een constante aan de uitbetalingen van een speler, of het vermenigvuldigen van de uitbetalingen van die speler met een positieve constante, geen invloed heeft op de Nash-evenwichten – zuiver of gemengd. Daarom kunnen we altijd één uitkomst voor elke speler nul laten zijn, en een andere uitkomst één. De enige vraag die overblijft is wat er gebeurt als geen van beide oplevert, in welk geval een crash het gevolg is. In deze versie is de uitbetaling vastgesteld op vier maal het verlies van uitwijken, zoals in Figuur 16.18 “Kip”, maar je kunt het spel veranderen en kijken wat er gebeurt.
Figuur 16.18 Kip
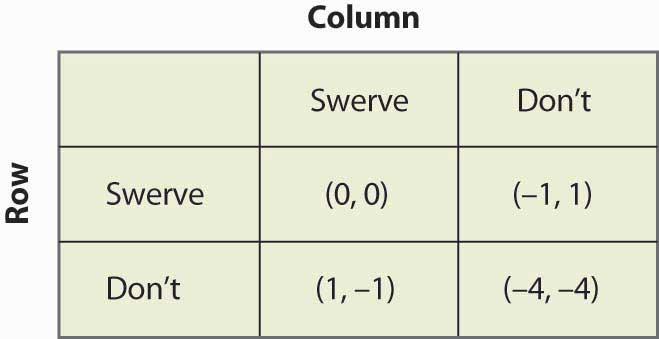
Dit spel heeft twee zuivere strategie-evenwichten: (Uitwijken, Niet) en (Niet, Uitwijken). Bovendien heeft het een gemengde strategie. Stel dat Kolom uitwijkt met kans p. Dan krijgt Rij 0p + -1(1 – p) van uitwijken, 1p + (-4)(1 – p) van niet uitwijken, en Rij zal randomiseren als deze gelijk zijn, waarvoor p = ¾ nodig is. Dat wil zeggen, de kans dat Kolom uitwijkt in een gemengde strategie evenwicht is ¾. Je kunt controleren of de rij-speler dezelfde kans heeft door de kans dat rij uitwijkt gelijk te stellen aan q en de verwachte uitbetalingen van kolom te berekenen. De kans op een botsing is dus 1/16 in het gemengde-strategie-evenwicht.
Het gemengde-strategie-evenwicht is in zekere zin waarschijnlijker in dit spel: Als de spelers al wisten wie zou toegeven, zouden ze het spel niet hoeven te spelen. Het doel van het spel is uit te vinden wie zal toegeven, wat betekent dat dit niet van tevoren bekend is. Dit betekent dat het gemengde-strategie-evenwicht in zekere zin het redelijker evenwicht is.
Figuur 16.19 Steen, papier, schaar
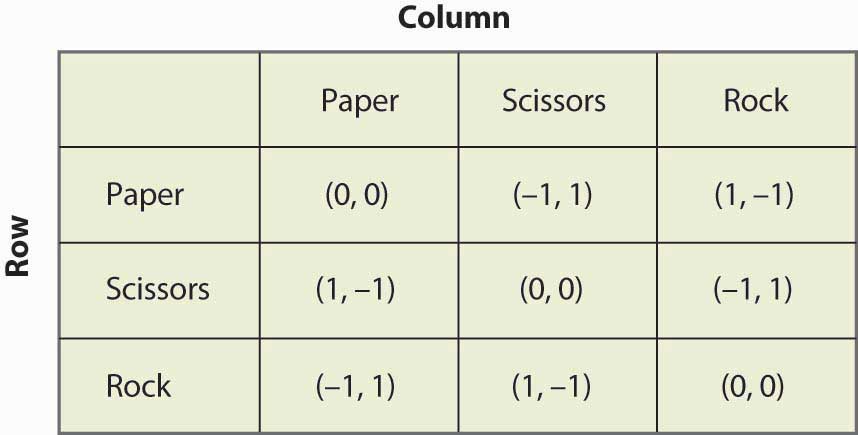
“Steen, papier, schaar” is een kinderspel waarbij twee kinderen hun handen gebruiken om tegelijkertijd papier (hand plat gehouden), schaar (hand met twee vingers uitgestoken om op een schaar te lijken), of steen (hand in een vuist) te kiezen. De aard van de uitbetalingen is dat papier beter is dan steen, steen beter dan schaar, en schaar beter dan papier. Dit spel heeft de structuur die wordt geïllustreerd in figuur 16.19 “Steen, papier, schaar”.
Key Takeaways
- Een mixed strategy Nash-evenwicht houdt in dat ten minste één speler een gerandomiseerde strategie speelt en dat geen enkele speler zijn of haar verwachte uitbetaling kan verhogen door een alternatieve strategie te spelen.
- Een Nash-evenwicht zonder randomisatie wordt een pure strategy Nash-evenwicht genoemd.
- Als een speler verondersteld wordt te randomiseren over twee strategieën, dan moeten beide dezelfde verwachte uitbetaling opleveren.
- Het matchen van centen spel heeft een gemengde strategie en geen zuivere strategie.
- Het slag der seksen spel heeft een gemengde strategie en twee zuivere strategieën.
- Het spel kip lijkt op de strijd der seksen en heeft net als het spel twee zuivere strategieën en één gemengde strategie.
Oefeningen
- Laat q de kans zijn dat Rij Kop speelt. Laat zien dat Kolom bereid is te randomiseren, als en slechts als q = ½. (Hint: Bereken eerst de verwachte uitbetaling van Kolom wanneer Kolom Kop speelt, en bereken dan de verwachte uitbetaling van Kolom wanneer Kolom Munt speelt. Deze moeten gelijk zijn wil Kolom randomiseren.)
- Ontdek dat er in het steen, papier, schaar-spel geen zuivere strategie-evenwichten zijn. Laat zien dat het spelen van alle drie de acties met gelijke waarschijnlijkheid een gemengde strategie-evenwicht is.
-
Vind alle evenwichten van de volgende spellen:
Figuur 16.20
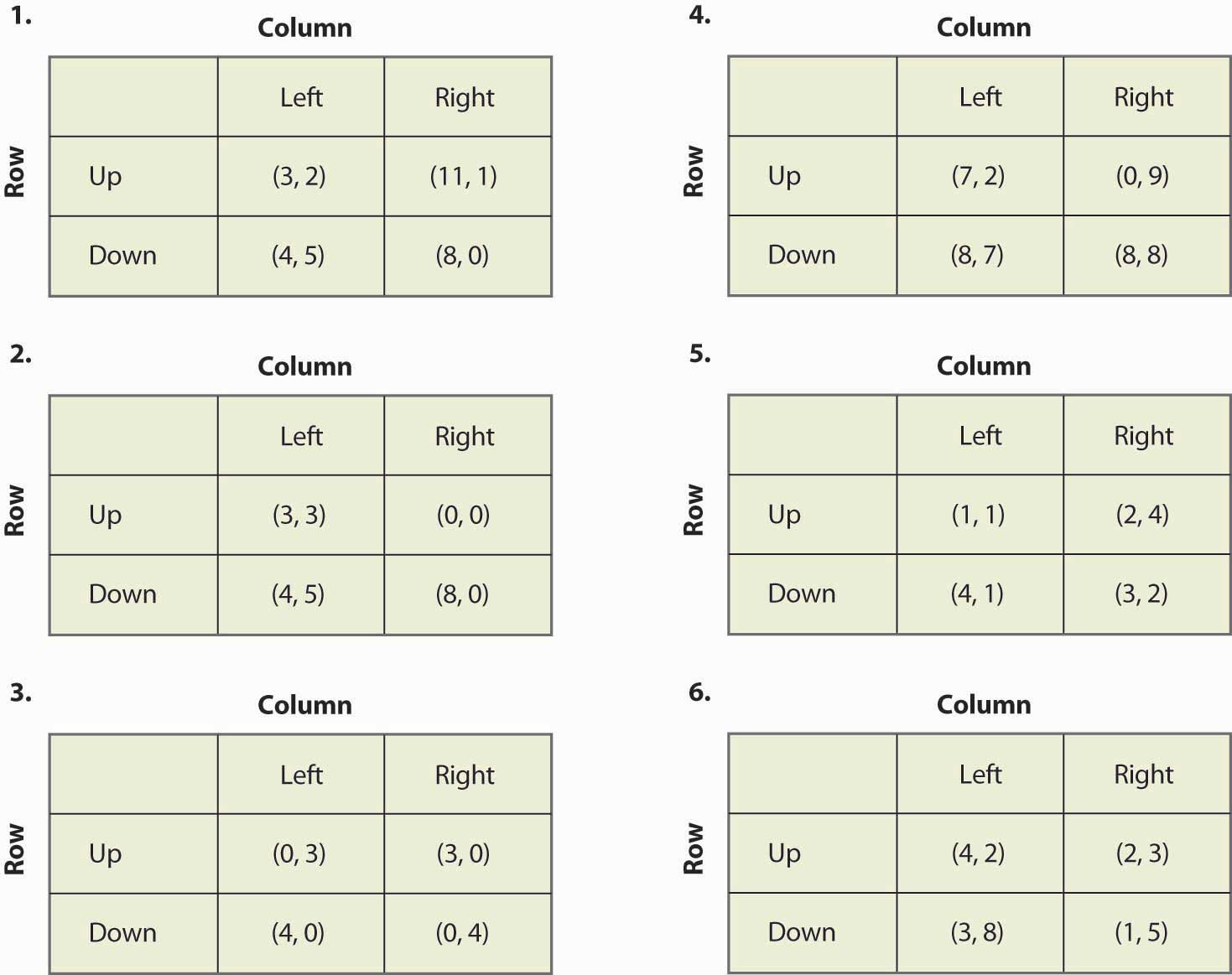
- Als je de uitbetaling van een speler vermenigvuldigt met een positieve constante, dan veranderen de evenwichten van het spel niet. Is dit waar of niet, en waarom?