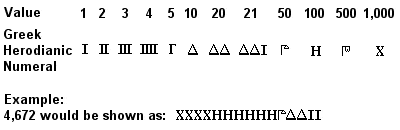
Ancient Greek Herodianic numerals
Toen het Griekse rijk zijn invloedssfeer begon uit te breiden naar Klein-Azië, Mesopotamië en verder, waren de Grieken slim genoeg om nuttige elementen uit de door hen veroverde samenlevingen over te nemen en aan te passen. Dit gold evenzeer voor hun wiskunde als voor iets anders, en zij namen elementen uit de wiskunde over van zowel de Babyloniërs als de Egyptenaren. Maar al snel begonnen zij zelf belangrijke bijdragen te leveren en voor het eerst kunnen wij bijdragen van individuen erkennen. In de Hellenistische periode hadden de Grieken een van de meest dramatische en belangrijke revoluties in het wiskundig denken aller tijden tot stand gebracht.
Attische of Herodiaanse cijfers
Het oude Griekse cijfersysteem, bekend als Attische of Herodiaanse cijfers, was rond 450 v. Chr. volledig ontwikkeld en werd mogelijk al in de 7e eeuw v. Chr. regelmatig gebruikt. Het was een op het vroegere Egyptische (en nog meer op het latere Romeinse) gebaseerd 10-tallig stelsel, met symbolen voor 1, 5, 10, 50, 100, 500 en 1.000, zo vaak herhaald als nodig was om het gewenste getal weer te geven. Het optellen gebeurde door het afzonderlijk optellen van de symbolen (1s, 10s, 100s, enz.) in de op te tellen getallen, en het vermenigvuldigen was een moeizaam proces gebaseerd op opeenvolgende verdubbelingen (het delen was gebaseerd op het omgekeerde van dit proces).
De onderscheppingstheorie van Thales
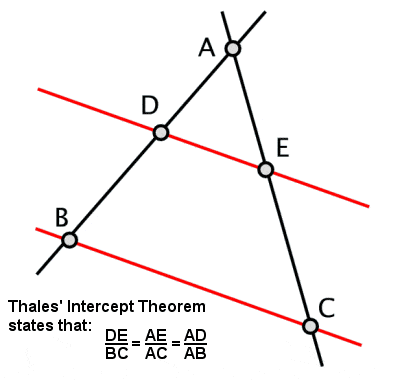
De onderscheppingstheorie van Thales
Maar het grootste deel van de Griekse wiskunde was gebaseerd op de meetkunde. Thales, een van de Zeven Wijzen van het Oude Griekenland, die in de eerste helft van de 6e eeuw v. Chr. aan de Ionische kust van Klein-Azië leefde, wordt gewoonlijk beschouwd als de eerste die richtlijnen heeft opgesteld voor de abstracte ontwikkeling van de meetkunde, hoewel wat we nu van zijn werk weten (zoals over gelijkvormige en rechthoekige driehoeken) nogal elementair lijkt.
Thales stelde vast wat bekend is geworden als de stelling van Thales, waarbij als een driehoek binnen een cirkel wordt getekend met de lange zijde als een diameter van de cirkel, de tegenoverliggende hoek altijd een rechte hoek zal zijn (evenals enkele andere verwante eigenschappen die hiervan zijn afgeleid). Hij wordt ook gecrediteerd met een andere stelling, ook bekend als de Stelling van Thales of de Onderscheppingstheorie, over de verhoudingen van de lijnstukken die ontstaan als twee snijdende lijnen worden onderschept door een paar parallellen (en, bij uitbreiding, de verhoudingen van de zijden van gelijksoortige driehoeken).
Tot op zekere hoogte is de legende van de 6e eeuw v. Chr. wiskundige Pythagoras van Samos echter synoniem geworden met de geboorte van de Griekse wiskunde. Van hem wordt aangenomen dat hij zowel de woorden “filosofie” (“liefde voor de wijsheid”) als “wiskunde” (“dat wat geleerd is”) bedacht heeft. Pythagoras was wellicht de eerste die zich realiseerde dat een compleet systeem van wiskunde kon worden geconstrueerd, waarbij geometrische elementen correspondeerden met getallen. De stelling van Pythagoras (of de stelling van Pythagoras) is een van de bekendste van alle wiskundige stellingen. Maar hij blijft een controversiële figuur, zoals we zullen zien, en de Griekse wiskunde was geenszins beperkt tot één man.
Drie meetkundige problemen
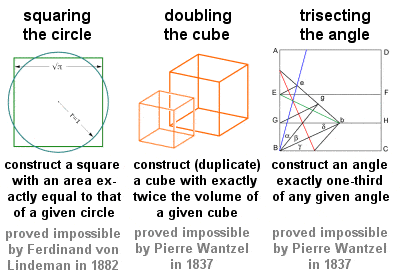
De Drie Klassieke Problemen
Drie meetkundige problemen in het bijzonder, die vaak de Drie Klassieke Problemen worden genoemd, en die alle met zuiver meetkundige middelen moeten worden opgelost met alleen een liniaal en een passer, stammen uit de begintijd van de Griekse meetkunde: “de kwadratuur van de cirkel, de verdubbeling van de kubus en de doorsnede van een hoek. Deze onverzettelijke problemen waren van grote invloed op de toekomstige meetkunde en leidden tot vele vruchtbare ontdekkingen, hoewel hun feitelijke oplossingen (of, zoals bleek, de bewijzen van hun onmogelijkheid) moesten wachten tot de 19e Eeuw.
Hippocrates van Chios (niet te verwarren met de grote Griekse arts Hippocrates van Kos. Een uitvoerige biografie is hier te vinden) was zo’n Griekse wiskundige die zich in de 5e Eeuw v. Chr. met deze problemen bezighield (zijn bijdrage aan het probleem van de “kwadratuur van de cirkel” staat bekend als de Lune van Hippocrates). Zijn invloedrijke boek “De Elementen”, dat dateert uit ongeveer 440 BCE, was de eerste compilatie van de elementen van de meetkunde, en zijn werk was een belangrijke bron voor het latere werk van Euclides.
Zeno’s Paradox van Achilles en de schildpad
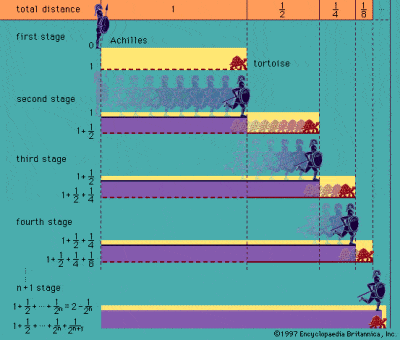
Zeno’s Paradox van Achilles en de schildpad
Het waren de Grieken die voor het eerst worstelden met het idee van oneindigheid, zoals beschreven in de bekende paradoxen die worden toegeschreven aan de filosoof Zeno van Elea in de 5e eeuw voor Christus. De beroemdste van zijn paradoxen is die van Achilles en de schildpad, waarin een theoretische wedloop tussen Achilles en een schildpad wordt beschreven. Achilles geeft de veel langzamere schildpad een voorsprong, maar tegen de tijd dat Achilles het beginpunt van de schildpad bereikt, heeft de schildpad al een voorsprong genomen. Tegen de tijd dat Achilles dat punt bereikt, is de schildpad weer verder, enz, enz, zodat de snelle Achilles de langzame schildpad in principe nooit kan inhalen.
Paradoxen als deze en Zeno’s zogenaamde Dichotomieparadox zijn gebaseerd op de oneindige deelbaarheid van ruimte en tijd, en berusten op het idee dat een half plus een kwart plus een achtste plus een zestiende, enz, enz, tot in het oneindige nooit helemaal gelijk zal zijn aan een geheel. De paradox komt echter voort uit de onjuiste veronderstelling dat het onmogelijk is om een oneindig aantal discrete streepjes te voltooien in een eindige tijd, hoewel het uiterst moeilijk is om deze denkfout definitief te bewijzen. De oude Griek Aristoteles was de eerste van velen die de paradoxen trachtte te weerleggen, vooral omdat hij er vast van overtuigd was dat oneindigheid alleen maar potentieel en niet reëel kon zijn.
Democritus, vooral bekend om zijn vooruitziende ideeën over het feit dat alle materie uit kleine atomen bestaat, was ook een pionier op het gebied van de wiskunde en de geometrie in de 5e – 4e eeuw voor Christus, en hij produceerde werken met titels als “Over Getallen”, “Over Geometrie”, “Over Tangencies”, “Over Mapping” en “Over Irrationalen”, hoewel deze werken niet bewaard zijn gebleven. We weten wel dat hij een van de eersten was die opmerkte dat een kegel (of piramide) een derde van het volume heeft van een cilinder (of prisma) met hetzelfde grondvlak en dezelfde hoogte, en hij is misschien de eerste die serieus heeft nagedacht over de verdeling van voorwerpen in een oneindig aantal doorsneden.
Het is echter zeker waar dat vooral Pythagoras een grote invloed heeft gehad op degenen die na hem kwamen, waaronder Plato, die in 387 v. Chr. zijn beroemde Academie in Athene oprichtte, en zijn beschermeling Aristoteles, wiens werk over de logica meer dan tweeduizend jaar lang als definitief werd beschouwd. Plato de wiskundige is vooral bekend om zijn beschrijving van de vijf Platonische vaste lichamen, maar de waarde van zijn werk als leraar en popularisator van de wiskunde kan niet worden overschat.
Plato’s leerling Eudoxus van Cnidus wordt gewoonlijk gecrediteerd voor de eerste toepassing van de “methode van uitputting” (later ontwikkeld door Archimedes), een vroege methode van integratie door opeenvolgende benaderingen die hij gebruikte voor de berekening van het volume van de piramide en de kegel. Hij ontwikkelde ook een algemene theorie van de proportie, die van toepassing was op incommensurabele (irrationele) grootheden die niet kunnen worden uitgedrukt als een verhouding van twee gehele getallen, maar ook op commensurabele (rationele) grootheden, waarmee hij de onvolledige ideeën van Pythagoras uitbreidde.
Misschien wel de belangrijkste bijdrage van de Grieken – en Pythagoras, Plato en Aristoteles waren in dit opzicht allemaal invloedrijk – was het idee van bewijsvoering, en de deductieve methode van het gebruiken van logische stappen om stellingen te bewijzen of te weerleggen vanuit aanvankelijk veronderstelde axioma’s. Oudere culturen, zoals de Egyptenaren en de Babyloniërs, vertrouwden op inductief redeneren, dat wil zeggen op het gebruik van herhaalde waarnemingen om vuistregels vast te stellen. Het is dit concept van bewijsvoering dat de wiskunde haar kracht geeft en ervoor zorgt dat bewezen theorieën vandaag nog even waar zijn als tweeduizend jaar geleden, en dat de basis legde voor de systematische benadering van de wiskunde van Euclides en degenen die na hem kwamen.
| << Terug naar Egyptische wiskunde | Voorwaarts naar Pythagoras >> |