Talking in Three Dimensions

Kijk eens naar dit plaatje van een rechthoekig prisma:

Hoeveel hoekpunten heeft het? 8

Hoeveel ribben? 12

Hoeveel zijvlakken? 6

Makkelijk, toch?

Laten we er nog een proberen. Kijk eens naar dit plaatje van een kegel:

Hoeveel hoekpunten heeft hij? Telt de punt aan de top mee?

Hoeveel ribben? Hmm, dat weet ik niet zeker. Horen randen niet recht te zijn?

Hoeveel zijvlakken? Da’s makkelijk! Een. Er is een rond gezicht aan de onderkant. Maar dat is geen veelhoek, dus is het nog steeds een gezicht? Oh, en hoe noem ik het andere oppervlak op de kegel? Moeten zijvlakken niet plat zijn?

Een veel voorkomende vraag die we krijgen van leraren in klas 1, 2, en 3 heeft te maken met hoe de eigenschappen van bepaalde driedimensionale vaste stoffen te beschrijven, met name cilinders en kegels. Volgens de TEKS moeten de leerlingen driedimensionale vaste lichamen beschrijven met formele meetkundige taal zoals hoekpunt, rand en vlak. Het probleem is dat we proberen taal te gebruiken die werkt voor één klasse van vormen om de eigenschappen van een heel andere klasse te beschrijven.

Drie-dimensionale vormen zoals prisma’s en piramides zijn veelvlakken. “In de meetkunde is een veelvlak eenvoudigweg een driedimensionaal vast lichaam dat bestaat uit een verzameling veelhoeken, meestal verbonden aan hun randen.” (Bron) Deze vaste lichamen hebben “vlakke veelhoekige zijvlakken, rechte randen, en gedeelde hoeken of hoekpunten.” (Bron)

Bollen, cilinders en kegels zijn daarentegen geen veelvlakken. Als gevolg daarvan kunnen we niet precies dezelfde taal gebruiken om ze te beschrijven, of als we wel dezelfde taal gebruiken, is dat met dien verstande dat de definities niet identiek zijn. Neem bijvoorbeeld het woord hoekpunt.

Op een rechthoekig prisma is een hoekpunt het scherpe punt of de hoek waar de ribben samenkomen. Een rechthoekig prisma heeft 8 hoekpunten.

Diezelfde term kan echter ook worden gebruikt om het punt van een kegel aan te duiden. Dezelfde term, maar niet dezelfde definitie. Zoals Dr. Math zegt,

Het lastige hier is dat het “hoekpunt” van een kegel niets te maken heeft met randen, en dus een heel nieuwe definitie nodig heeft; en ik kan geen echt goede definitie op basisschoolniveau bedenken voor wat ze duidelijk bedoelen, namelijk gewoon een “punt.”

Als leerlingen meer gevorderde wiskunde gaan doen, kunnen ze meer verfijnde taal en definities ontwikkelen. In de tussentijd, zolang ze nog op de basisschool zitten, gebruiken we in RRISD de term hoekpunt van een kegel om dit kenmerk van een kegel aan te duiden.

Als we willen dat leerlingen dit soort driedimensionale vaste stoffen beschrijven en classificeren, dan moeten we daarvoor toegankelijke taal aanreiken.

Hoe zit het met de andere kenmerken van een kegel? Ook hier is het ons doel een taal te geven die toegankelijk is voor leerlingen in het basisonderwijs en die deze eigenschappen beschrijft, in het besef dat onze leerlingen later in hun schoolloopbaan een formeler begrip zullen ontwikkelen. Om een kegel te beschrijven, zouden we zeggen dat hij een ronde basis heeft, het platte oppervlak waarop de kegel rust. We zeggen ook dat hij een gebogen rand heeft langs de basis en een gebogen oppervlak dat van deze rand tot aan het hoekpunt loopt.

Hoe zit het met een cilinder? Nu we een toegankelijke taal hebben om eigenschappen van een kegel te beschrijven, kunnen we deze taal uitbreiden om eigenschappen van cilinders te beschrijven.

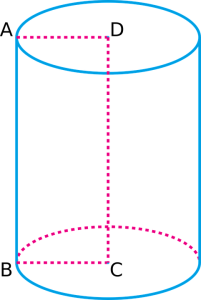
De bovenstaande cilinder bestaat uit twee cirkelvormige grondvlakken, een aan de bovenkant en een aan de onderkant. Hij heeft ook twee gebogen randen, een langs de bovenkant en een langs de onderkant. Tenslotte heeft zij een gebogen oppervlak dat zich uitstrekt van de onderrand tot aan de bovenrand.

Ik moet hieraan toevoegen dat zowel de kegel als de cilinder die ik heb beschreven een rechtse cirkelkegel en een rechtse cilinder zijn. Net als bij veelhoeken en veelvlakken zijn er vele andere soorten voorbeelden van deze vormen. De kegel of cilinder kan bijvoorbeeld schuin staan, waardoor ze schuin worden.

Het is belangrijk voor leerlingen om een verscheidenheid aan voorbeelden van twee- en driedimensionale figuren te zien. Hoe meer ze er tegenkomen, hoe meer ze geconfronteerd worden met hun definities en terminologie, wat hun begrip van de attributen versterkt en hoe deze ons helpen deze figuren te identificeren en te classificeren.

Zo hoe ziet dit eruit op STAAR?

Op de in 2016 vrijgegeven test stelde STAAR een vraag die precies dit onderwerp behandelde en de woordenschat versterkte die we in RRISD gebruiken.

Het juiste antwoord is F Ze hebben geen hoekpunten. Als je naar set B kijkt, zie je dat deze een kegel bevat, die zoals we eerder bespraken wel een hoekpunt heeft. Als het Texas Education Agency de term hoekpunt van een kegel niet zou gebruiken, dan hadden we de kegel waarschijnlijk wel in reeks A gezien.

Hier volgt een afscheidsgedachte van Dr. Math:

Welke definitie je gebruikt, hangt af van wat je ermee gaat doen. Als je alleen objecten beschrijft, is mijn losse definitie prima. Als je stellingen gaat bewijzen die te maken hebben met vlakken en hoeken, zul je je willen beperken tot de veelhoeksdefinitie, maar dan zul je geen vragen stellen over kegels. Ik denk dat mensen vaak niet beseffen dat, ook al zijn we in de wiskunde kieskeurig over definities, die definities verschillen van gebied tot gebied, omdat ze aangepast zijn aan een bepaalde context. Dat is wat ik hier probeer te doen.