Ce este o rețea?
O rețea este o matrice ordonată de puncte care descrie aranjamentul particulelor care formează un cristal.
Celula unitară a unui cristal este definită de punctele rețelei.Celula unitară este cea mai mică parte a unui cristal care, repetată în mod regulat prin translație în trei dimensiuni, creează întregul cristal.
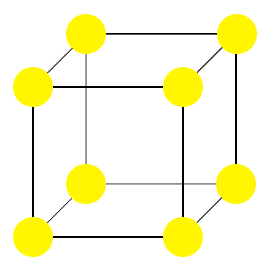
De exemplu, imaginea prezentată aici este celula unitară a unei structuri cubice primitive.
În structura desenată, toate particulele (galbene) sunt identice.În acest caz particular, punctele de rețea care definesc celula unitară coincid cu centrele particulelor cristalului. Acest lucru nu trebuie să fie întotdeauna cazul.
Rețeaua ionică
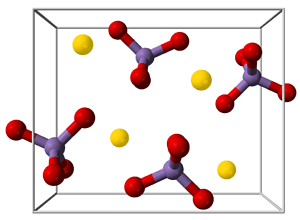
Dacă un cristal este format din ioni, compusul poate fi descris ca o rețea ionică.
Exemple bine cunoscute de rețele ionice sunt clorura de sodiu, permanganatul de potasiu, boraxul (borat de sodiu) și sulfatul de cupru(II).

Rețeaua covalentă
Dacă un cristal este alcătuit din atomi legați covalent, poate fi descris ca o rețea covalentă sau rețea covalentă infinită.
Exemple bine cunoscute de rețele covalente sunt diamantul, cuarțul (dioxidul de siliciu), siliciul și staniul gri.
Constantele rețelei
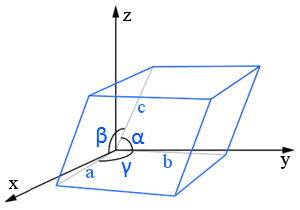
Constantele rețelei (sau parametrii rețelei) sunt lungimile și unghiurile dintre marginile celulei unitare.
În această diagramă de rețea paralelipipedică, constantele de rețea sunt a, b și c (lungimi) și α, β și γ (unghiuri).
Structuri de rețea
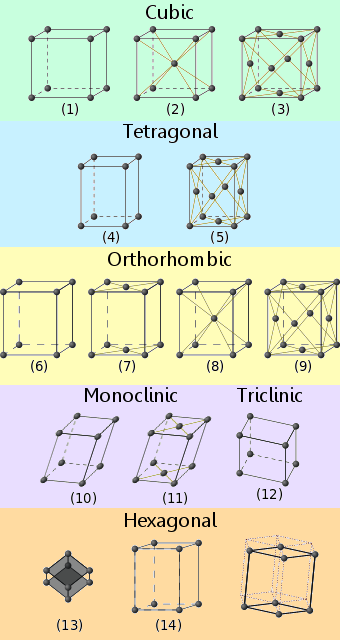
Materialele cristaline se încadrează într-unul din cele paisprezece aranjamente de rețele recunoscute.Acestea sunt cunoscute sub numele de rețele Bravais.
Numele sistemelor de rețele cristaline, care corespund numerelor de pe diagrame, sunt următoarele:
1. Cubic primitiv
2. Cubic centrat pe corp
3. Cubic centrat pe față
4. Tetragonal primitiv
5. Tetragonal primitiv
6. Tetragonal centrat pe corp
6. Ortorombic primitiv
7. Ortorombic centrat pe bază
8. Ortorombic centrat pe corp
9. Ortorombic centrat pe corp
9. Orthorhombic centrat pe față
10. Monoclinic primitiv
11. Monoclinic centrat pe bază
12. Triclinic
13. Romboedrică
14. Hexagonal
Defecte de rețea
Dacă s-ar presupune că un cristal se bazează pe o rețea ionică perfectă din punct de vedere matematic, rezistența sa la tracțiune calculată ar fi mult mai mare decât cea observată în realitate.
.